Econometrics

Question 1

Typical Problems Estimating Economic Models - High multicollinearity

Answer 1

Definition: Two or more independent variables in a regression model exhibit a close linear relationship.

Consequences:

• Large standard errors and insignificant t-statistics
• Coefficient estimates sensitive to minor changes in model specification
• Nonsensical coefficient signs and magnitudes

Detection:

• Pairwise correlation coefficients
• Variance inflation factor (VIF)

Solution:

• Collect additional data.
• Re-specify the model.
• Drop redundant variables.

Question 2

Typical Problems Estimating Economic Models - Heteroskedasticity

Answer 2

Definition: The variance of the error term changes in response to a change in the value of the independent variables.

Consequences:

• Inefficient coefficient estimates
• Biased standard errors
• Unreliable hypothesis tests

Detection:

• Park test
• Goldfeld-Quandt test
• Breusch
• Pagan test
• White test

Solution:

• Weighted least squares (WLS)
• Robust standard errors

Question 3

Typical Problems Estimating Economic Models - Autocorrelation

Answer 3

Definition: An identifiable relationship (positive or negative) exists between the values of the error in one period and the values of the error in another period.

Consequences:

• Inefficient coefficient estimates
• Biased standard errors
• Unreliable hypothesis tests

Detection:

• Geary or runs test
• Durbin-Watson test
• Breusch-Godfrey test

Solution:

• Cochrane-Orcutt transformation
• Prais-Winsten transformation
• Newey-West robust standard errors

Question 4

Rules for the mean

Answer 4

Question 5

Rules for the variance

Answer 5

Question 6

Rules for the covariance

Answer 6

• Let X, Y, and V be random variables; let mX and s2X be the mean and variane of X and let sXY be the covariance between X and Y; and let a, b, and c constants. The following rules follow:
  
  • E(a + bX + cY) = a + bm_X + cm_y
  • Var(a + bY) = b²s²_Y
  • Var(aX + bY) = as²_X + 2abs_XY + b²s²_Y
  • E(Y²) = s²_Y + m²_y
  • Cov(a + bX + cV, Y) = bs_XY + cs_VY
  • E(XY) = s_XY + m_xm_y

corr(X,Y) | ≤ 1 and |s_XY| ≤ Ös²_Xs²_Y (correlation inequality)

Question 7

Formulas variance, covariance, sd

Answer 7

Question 8

Rules correlation

Answer 8

Question 9

Limit for unusual data

Answer 9

Below : µ-2σ

Above: µ+2σ

Question 10

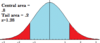
Empirical rule for normal distribution

Answer 10

About 68% of the data falls within: µ-σ to µ+σ

About 95%: µ-2σ to µ+2σ

About 99.7%:µ-3σ to µ+3σ

Question 11

Least-squares line coefficients

Answer 11

Question 12

Modified boxplot outliers

Answer 12

Question 13

Why use panel data in regression?

Answer 13

• using panel data is one way of controlling for some types of omitted variables without actually observing them

Question 14

panel data definition

Answer 14

• panel data: data in which each observatioal unit, or entity. is observed at two or more time periods; by studying changes in the dependent variable over time, it is possible to eliminate th effect of omitted varibales that differ across entities but are constant over time; more formally: data for n different entities observed at T different time periods
• example: effet of alcohol taxes and drunk driving laws on traffic fatalities in the US: use data across states over multiple years - this lets us control for unobserved variables that differ from one state to the next but do not change over time, e.g. cultural attitudes toward drinking and driving. It also allows us to control for variables that vary through time, but do not vary across states, e.g. improvements in the safety of new cars.

Question 15

cross-sectional data

Answer 15

• Cross-sectional data, or a cross section of a study population, is data collected by observing many subjects at one point or period of time. Analysis of cross-sectional data usually consists of comparing the differences among selected subjects.
• Cross-sectional data differs from time series data, in which the entity is observed at various points in time. Another type of data, panel data (or longitudinal data), combines both cross-sectional and time series data ideas and looks at how the subjects (firms, individuals, etc.) change over a time series.

Question 16

balanced / unbalanced panel

Answer 16

balanced: has all its observations, i.e. varibales are observed for each entity and each time period

Question 17

panel data: before / after comparisons

Answer 17

by focusing on changes in the dependent variable over time, this differences comparison holds constant the onobserved factors tht differ from one state to the next but do not change over time within the state

Question 18

how panel data eliminates effect of unobserved variables that do not change over time

Answer 18

because Z_i (e.g. attitude toward drinking and driving) does not change over time, it will not produce any change in the fatality rate between two time periods. Thus, in the regression model, the influence of Z_i can be eliminated by analyzing the change in the dependent variable between the two periods. If there is a difference between the two y-values, the change must have come from ohter sources, e.g. your independent variables or your error terms

Question 19

why include an intercept?

Answer 19

allows for the possibility that the mean change in e.g. the fatality rate, in the abscence of a change in the real beer tax, is nonzero. For example, a negative intercept could reflect improvements in auto safety between two time periods that reduced the average fatality rate

Question 20

does “before and after” method work for T>2?

Answer 20

not directly; to analyze all the observations in a panel data set, use the method of fixed effets regression

Question 21

fixed effects regression

Answer 21

is a method for controlling for omitted variables in panel data when the omitted variables vary across entities, but do not change over time; T can be greater than 2

Question 22

fixed effects regression model

Answer 22

Question 23

entitity-specific intercepts as binary variables

Answer 23

Question 24

entity-demeaned OLS algorithm

Answer 24

Question 25

regression with time fixed effects only

Answer 25

Question 26

entity and time fixed effects

Answer 26

Question 27

regression error in panel data

Answer 27

can be correlated over time within an entity. Like heteroskedasticity, this correlation does not introduce bias in the fixed effects estimator, but it affects the variance of the fixed effects estimator, and therefore how one computes the standard errors

Question 28

difference in regression assumptions between panel data and cross-sectional data

Answer 28

cross-sectional: each observation is independent, which arises under simple random sampling; in contrast, with panel data the variables are independent across entities but makes no such restriction within an entity; X_it can be correlated over time within an entity; if this applies to X_it then it is also known as autocorrelated or serially correlated; this is a pervasieve eture of time series data: what happens in one year tends to be correlated with what hapens in the next year; same applies to u_it

Question 29

standard errors for fixed effects regression

Answer 29

if regression errors are autocorrelated, then the usual heteroskedasticiy-robust SE formula for cross-section regression is not valid; SE that are valid if u_it is potentially heteroskedastic and potentially correlated over time within an entity, are referred to as heteroskedasticity-and-autocorrelation-robust SE; we use one type of those, clustered SEs

Question 30

clustered SEs

Answer 30

• Solution to issue that errors might be correlated over time: compute HAR- or Clustered-se’s
  
  • Heteroskedasticity-and Autocorrelation-robust (also consistent, HAC)
  • Allows for arbitrary correlation within clusters (entities i), but assumes no correlation across entities
• HAR se’s also consistent if no heteroskedasticity and/or no autocorrelation present
• HAR is biased, however, when number of entities is small (i.e. below 42), even with large T
• In stata:

command Y X, cluster(entity)

• in the context of panel data, each cluster consists of an entity; thus clustered SEs allow for heteroskedasticity and for arbitrary autocorrelation within an entity but treat the errors as uncorrelated across entities
• if the number of entities n is large, inference using clustered SEs can proceed using the usual large-sample normal critical values for t-statistics and F critical values for F-statistics testing q restrictions
• Not correcting for autocorrelation, i.e. not clustering in panel data regression, leads to standard errors which (usually) too low (can see this in regression outputs - compare SEs for regression with and without clustering

Question 31

when 0 is included in CI

Answer 31

hypothesis that the independent variable has no effect on y cannot be rejected at the x% significance level

Question 32

Quasi experiments: when real experiments aren’t feasible

Answer 32

• having a control group is unethical (e.g. giving ill people a placebo medication)
• examining effects that rely on person-factors
  
  • cannot randomly assign peopel to be introverted etc.
  • any experiment examining person-factors is not a true experiment (because such factors cannot be randomly assinged)

Question 33

confounding variable

Answer 33

• “extra” variable that you didn’t account for. They can ruin an experiment and give you useless results. Confounding variables are any other variables besides your independent variable that have an effect on your dependent variable
• example: estimate effect of activity level on weight gain, a counfounding variable would be age, how much you eat etc.
• two major problems
  
  • increase variance
  • introduce bias

Question 34

Confounding bias

Answer 34

• result of having confounding variables in your model. It has a direction, depending on if it over- or underestimates the effects of your model:
  
  • Positive confounding: observed association is biased away from the null, i.e. it overestimates the effect.
  • Negative confounding: observed association is biased toward the null, i.e. it underestimates the effect.

Question 35

how to reduce confounding variables

Answer 35

• Bias can be eliminated with random samples.
• Introduce control variables to control for confounding variables, e.g. control for age by only measuring 30 year olds
• Counterbalancing can be used if you have paired designs. In counterbalancing, half of the group is measured under condition 1 and half is measured under condition 2.

Question 36

internal validity

Answer 36

way to measure if research is sound. It is related to how many confounding variables you have in your experiment

Question 37

external vs. internal validity

Answer 37

Internal validity is a way to gauge how strong your research methods were. External validity helps to answer the question: can the research be applied to the “real world”?

Question 38

things that can affect validity

Answer 38

• Regression to the mean. This means that subjects in the experiment with extreme scores will tend to move towards the average.
• Pre-testing subjects. This may have unexpected consequences as it may be impossible to tell how the pre-test and during-tests interact. If “logical reasoning” is your dependent variable, participants may get clues from the pre-test.
• Changing the instruments during the study.
• Participants dropping out of the study. This is usually a bigger threat for experimental designs with more than one group.
• Failure to complete protocols.
• Something unexpected changes during the experiment, affecting the dependent variable.

Question 39

measurement error

Answer 39

• difference between a measured quantity and its true value. It includes random error (naturally occurring errors that are to be expected with any experiment) and systematic error (caused by a mis-calibrated instrument that affects all measurements).
• For example, let’s say you were measuring the weights of 100 marathon athletes. The scale you use is one pound off: this is a systematic error that will result in all athletes body weight calculations to be off by a pound. On the other hand, let’s say your scale was accurate. Some might have wetter clothing or a 2 oz. candy bar in a pocket. These are random errors and are to be expected. In fact, all collected samples will have random errors — they are, for the most part, unavoidable.

Question 40

different measures of error

Answer 40

• Absolute Error: the amount of error in your measurement. For example, if you step on a scale and it says 150 pounds but you know your true weight is 145 pounds, then the scale has an absolute error of 150 lbs – 145 lbs = 5 lbs.
• Greatest Possible Error: defined as one half of the measuring unit, e.g. if measures in whole yards, then the greatest possible error is one half yard.
• Instrument Error: error caused by an inaccurate instrument (like a scale that is off or a poorly worded questionnaire).
• Margin of Error: an amount above and below your measurement. For example, you might say that the average baby weighs 8 pounds with a margin of error of 2 pounds (± 2 lbs).
• Measurement Location Error: caused by an instrument being placed somewhere it shouldn’t, like a thermometer left out in the sun
• Operator Error: human factors that cause error, like reading a scale incorrectly.
• Percent Error: another way of expressing measurement error. Defined as: percent-error = (measured value – actual value)/actual value
• Relative Error: the ratio of the absolute error to the accepted measurement. As a formula, that’s: E(relative) = E(absolute)/E(measured)

Question 41

ways to reduce measurement error

Answer 41

• Double check all measurements & formulas
• Make sure observers are well trained.
• Make the measurement with the instrument that has the highest precision.
• Take measurements under controlled conditions.
• Pilot test your measuring instruments, e.g. put together a focus group and ask how easy or difficult the questions were to understand.
• Use multiple measures for the same construct. For example, if you are testing for depression, use two different questionnaires.

Question 42

statistical procedures to assess measurement error

Answer 42

• Standard error of measurement (SEM): estimates how repeated measurements taken on the same instrument are estimated around the true score.
• Coefficient of variation (CV): a measure of the variability of a distribution of repeated scores or measurements. Smaller values indicate a smaller variation and therefore values closer to the true score.
• Limits of agreement (LOA): gives an estimate of the interval where a proportion of the differences lie between measurements.

Question 43

simultaneity bias

Answer 43

• where the explanatory variable is jointly determined with the dependent variable, i.e. X causes Y but Y also causes X. It is one cause of endogeneity (the other two are omitted variables and measurement error).
• A similar bias is reverse causation, where Y causes X (but X does not cause Y).
• Simultaneity bias is a term for the unexpected results that happen when the explanatory variable is correlated with the regression error term, ε (sometimes called the residual disturbance term), because of simultaneity. It’s so similar to omitted variables bias that the distinction between the two is often very unclear and in fact, both types of bias can be present in the same equation.
• The standard way to deal with this type of bias is with IV regression (e.g. two stage least squares).

Question 44

simultaneity bias causes

Answer 44

• Changes in a RHS variable are causing changes in a LHS variable.
• Variables on LHS and RHS are jointly determined.

Question 46

reverse causality

Answer 46

Instead of X causing a change in Y, it is really the other way around: Y is causing changes in X

Question 47

estimator properties

Answer 47

Question 48

multicollinearity

Answer 48

• occurs when there are high correlations between two or more predictor variables. In other words, one predictor variable can be used to predict the other. This creates redundant information, skewing the results in a regression model.
• Examples: a person’s height and weight, age and sales price of a car

Question 49

how to detect multicollinearity

Answer 49

• calculate correlation coefficients for all pairs of predictor variables. If the correlation coefficient, r, is exactly +1 or -1, this is called perfect multicollinearity. If r is close to or exactly -1 or +1, one of the variables should be removed from the model if at all possible.
• Variance inflation factor (VIF)

Question 50

consequences of multicollinearity

Answer 50

• The partial regression coefficient may be an imprecise estimate; SEs may be very large.
• Partial regression coefficients may have sign and/or magnitude changes as they pass from sample to sample.
• makes it difficult to gauge the effect of independent variables on dependent variables
• The t-statistic will generally be very small, i.e. insignificant, and coefficient CIs will be very wide. This means that it is harder to reject the null hypothesis.
• Coefficient estimates sensitive to minor changes in model specification

Question 51

reasons for multicollinearity

Answer 51

• Data-based multicollinearity: caused by poorly designed experiments, data that is 100% observational, or data collection methods that cannot be manipulated. In some cases, variables may be highly correlated (usually due to collecting data from purely observational studies) and there is no error on the researcher’s part. For this reason, you should conduct experiments whenever possible, setting the level of the predictor variables in adance.
• Structural multicollinearity: caused by you, the researcher, creating new predictor variables.
• Dummy variables may be incorrectly used. For example, the researcher may fail to exclude one category, or add a dummy variable for every category (e.g. spring, summer, autumn, winter).
• Including a variable in the regression that is actually a combination of two other variables, e.g. including “total investment income” when total investment income = income from stocks and bonds + income from savings interest.
• Including two (almost) identical variables, e.g. weight in pounds and weight in kilos
• Insufficient data. In some cases, collecting more data can resolve the issue.

Question 52

heteroskedasticity

Answer 52

• The variance of the error term changes in response to a change
  in the value of the independent variables, i.e. the variance of the conditional distribution of u given X is constant
  • example: if x is higher social class of father and y is earnings of son, homoskedasticity implies that the variance of the error term is the same for people with father from higher socioeconomic class and for those whose father’s socioeconomic classfiication was lower
• Heteroscedastic data tends to follow a cone shape on a scatter graph.
• if you’re running any kind of regression analysis, having data that shows heteroscedasticity can ruin your results (at the very least, it will give you biased coefficients).
• In regression, an error is how far a point deviates from the regression line. Ideally, your data should be homoscedastic (i.e. the variance of the errors should be constant). This rarely happens. Most data is heteroscedastic by nature, e.g. predicting women’s weight from their height. In a Stepford Wives world, where everyone is a perfect dress size 6, this would be easy: short women weigh less than tall women. But it’s practically impossible to predict weight from height. Younger women (in their teens) tend to weigh less, while post-menopausal women often gain weight. But women of all shapes and sizes exist over all ages. This creates a cone shaped graph for variability. Plotting variation of women’s height/weight would result in a funnel that starts off small and spreads out as you move to the right of the graph. However, the cone can be in either direction:
  
  • Cone spreads out to the right: small values of X give a small scatter while larger values of X give a larger scatter with respect to Y.
  • Cone spreads out to the left: small values of X give a large scatter while larger values of X give a smaller scatter with respect to Y.

Question 53

how to detect heteroskedasticity

Answer 53

• A residual plot can suggest (but not prove) heteroscedasticity. Residual plots are created by:
  
  • Calculating the square residuals.
  • Plotting the squared residuals against an explanatory variable (one that you think is related to the errors).
  • Make a separate plot for each explanatory variable you think is contributing to the errors.
• Several tests can also be run:
  
  • Park Test
  • White Test
  • Goldfeld-Quandt test
  • Breusch
  • Pagan test

Question 54

consequences of heteroskedasticity

Answer 54

• OLS will not give you the estimator with the smallest variance (i.e. your estimators will not be useful).
• Significance tests will run either too high or too low.
• Standard errors will be biased, along with their corresponding test statistics and confidence intervals.

Question 55

how to deal with heteroskedastic data

Answer 55

• Give data that produces a large scatter less weight, i.e. weighted least squares
• Transform the Y variable to achieve homoscedasticity. For example, use the Box-Cox normality plot to transform the data.
• robust standard errors

Question 56

how to deal with multicollinearity

Answer 56

• Collect additional data.
• Re-specify the model.
• Drop redundant variables

Question 57

autocorrelation

Answer 57

An identifiable relationship (positive or negative) exists between the values of the error in one period and the values of the error in another period.

Question 58

autocorrelation consequences

Answer 58

• Inefficient coefficient estimates
• Biased standard errors
• Unreliable hypothesis tests

Question 59

how to detect autocorrelation

Answer 59

• Geary or runs test
• Durbin-Watson test
• Breusch-Godfrey test

Question 60

how to deal with autocorrelation

Answer 60

• Cochrane-Orcutt transformation
• Prais-Winsten transformation
• Newey-West robust standard errors

Question 61

intuition behind variance & bias

Answer 61

Question 62

covariance vs. correlation

Answer 62

• covariance: measure used to indicate the extent to which two random variables change in tandem.
• correlation: measure used to represent how strongly two random variables are related
• Covariance is nothing but a measure of correlation. On the contrary, correlation refers to the scaled form of covariance.
• The value of correlation takes place between -1 and +1. Conversely, the value of covariance lies between -∞ and +∞.
• Correlation is not affected by change in scale, but covariance is, i.e. if all the value of one variable is multiplied by a constant and all the value of another variable are multiplied, by a similar or different constant, then the covariance is changed.
• Correlation is dimensionless, i.e. it is a unit-free measure of the relationship between variables. Unlike covariance, where the value is obtained by the product of the units of the two variables.
• Covariances are hard to compare: when you calculate the covariance of a set of heights and weights, as expressed in meters and kilograms, you will get a different covariance from when you do it in other units, but also, it will be hard to tell if (e.g.) height and weight ‘covary more’ than, say the length of your toes and fingers, simply because the ‘scale’ the covariance is calculated on is different.
• The solution to this is to ‘normalize’ the covariance: you divide the covariance by something that represents the diversity and scale in both the covariates, and end up with a value that is assured to be between -1 and 1: the correlation. Whatever unit your original variables were in, you will always get the same result, and this will also ensure that you can, to a certain degree, compare whether two variables ‘correlate’ more than two others, simply by comparing their correlation.

Question 63

what is a hypothesis

Answer 63

an educated guess about something in the world around you. It should be testable, either by experiment or observation.

Question 64

a good hypothesis should contain:

Answer 64

• Include an “if” and “then” statement
• Include both the independent and dependent variables.
• Be testable by experiment, survey or other scientifically sound technique.
• Be based on information in prior research (either yours or someone else’s).
• Have design criteria (for engineering or programming projects).

Question 65

hypothesis testing

Answer 65

• a way for you to test the results of a survey or experiment to see if you have meaningful results. You’re basically testing whether your results are valid by figuring out the odds that your results have happened by chance. If your results may have happened by chance, the experiment won’t be repeatable and so has little use.
• approach
  
  • Figure out your null hypothesis,
  • State your null hypothesis,
  • Choose what kind of test you need to perform,
  • Either support or reject the null hypothesis.

Question 66

what is a null hypothesis?

Answer 66

• set the null-Hypothesis to the outcome you do not want to be true i.e. the outcome whose direct opposite you want to show.
• Basic example: Suppose you have developed a new medical treatment and you want to show that it is indeed better than placebo. So you set Null-Hypothesis H0:=new treament is equal or worse than placebo and Alternative Hypothesis H1:=new treatment is better than placebo.
• This because in the course of a statistical test you either reject the Null-Hypothesis (and favor the Alternative Hypothesis) or you cannot reject it. Since your “goal” is to reject the Null-Hypothesis you set it to the outcome you do not want to be true.
• The null hypothesis, H0 is the commonly accepted fact; it is the opposite of the alternate hypothesis. Researchers work to reject, nullify or disprove the null hypothesis. Researchers come up with an alternate hypothesis, one that they think explains a phenomenon, and then work to reject the null hypothesis.
• null comes from nullifiable, i.e. something you can invalidate

Question 67

p-value

Answer 67

• it’s the smallest significance level at which the null hypothesis could be rejected
• used in hypothesis testing to help you support or reject the null hypothesis. The p value is the evidence against a null hypothesis. The smaller the p-value, the stronger the evidence that you should reject the null hypothesis, i.e. a 0.02 (2%) p-value means that there is a 2% chance that your results could be random
• p-value is the probability of drawing a statistic at least as adverse to the null hypothesis as the one you actually computed. Equivalently, the p-value is the smallest significance level at which you can reject the null hypothesis.
• When you run a hypothesis test, you compare the p value from your test to the alpha level you selected when you ran the test. Alpha levels can also be written as percentages.
• Graphically, the p value is the area in the tail of a probability distribution. It’s the area to the right of the test statistic (if you’re running a two-tailed test, it’s the area to the left and to the right).

Question 68

p-value vs alpha level

Answer 68

• Alpha levels are controlled by the researcher and are related to confidence levels. You get an alpha level by subtracting your confidence level from 100%, e.g. if you want to be 98% confident in your research, the alpha level would be 2%. When you run the hypothesis test, the test will give you a value for p. Compare that value to your chosen alpha level, e.g. say you chose alpha=5%. If the results from the test give you:
• A small p (≤ 0.05), reject the null hypothesis. This is strong evidence that the null hypothesis is invalid.
• A large p (> 0.05) means the alternate hypothesis is weak, so you do not reject the null.

Question 69

p-values and critical values

Answer 69

• The p value is just one piece of information you can use when deciding if your null hypothesis is true or not. You can use other values given by your test to help you decide, e.g. if you run an f test two sample for variances, you’ll get a p value, an f-critical value and a f-value.
• Large p-value–>not reject the null. However, there’s also another way you can decide: compare your f-value with your f-critical value. If the f-critical value is smaller than the f-value, you should reject the null hypothesis

Question 70

critical value

Answer 70

A critical value is a line on a graph that splits the graph into sections. One or two of the sections is the “rejection region”; if your test value falls into that region, then you reject the null hypothesis.

It’s the value of the statistic for which the test just rejects the null hypothesis at the given significance level

Question 71

critical value of z

Answer 71

• is term linked to the area under the standard normal model. Critical values can tell you what probability any particular variable will have.
• the graph has two regions
  
  • Central region: The z-score is equal to the number of sds from the mean. A score of 1.28 indicates that the variable is 1.28 sds from the mean. If you look in the z-table for a z of 1.28, you’ll find the area is .3997. This is the region to the right of the mean, so you’ll double it to get the area of the entire central region: .3997*2 = .7994 or about 80%.
  • Tail region: The area of the tails (the red areas) is 1 minus the central region. In this example, 1-.8=.20, or about 20 percent. The tail regions are sometimes calculated when you want to know how many variables would be less than or more than a certain figure.

Question 72

when are critical values of z used?

Answer 72

A critical value of z (Z-score) is used when the sampling distribution is normal, or close to normal. Z-scores are used when the population standard deviation is known or when you have larger sample sizes. While the z-score can also be used to calculate probability for unknown standard deviations and small samples, many statisticians prefer to use the t distribution to calculate these probabilities.

Question 73

other uses of z-score

Answer 73

• Every statistic has a probability, and every probability calculated for a sample has a margin of error. The critical value of z can also be used to calculate the margin of error.
• Margin of error = Critical value * Standard deviation of the statistic
• Margin of error = Critical value * Standard error of the sample

Question 74

finding z-score for a CI example

Answer 74

• Find a critical value for a 90% confidence level (Two-Tailed Test).
• Step 1: Subtract the confidence level from 100% to find the α level: 100% – 90% = 10%.
• Step 2: Convert Step 1 to a decimal: 10% = 0.10.
• Step 3: Divide Step 2 by 2 (this is called “α/2”).
• 0.10 = 0.05. This is the area in each tail.
• Step 4: Subtract Step 3 from 1 (because we want the area in the middle, not the area in the tail):
• 1 – 0.05 = .95.
• Step 5: Look up the area from Step in the z-table. The area is at z=1.645. This is your critical value for a confidence level of 90%

Question 75

find a critical value: two-sided test

Answer 75

• Find the critical value for alpha of .05.
• Step 1: Subtract alpha from 1: 1 – .05 = .95
• Step 2: Divide Step 1 by 2 (because we are looking for a two-tailed test): .95 / 2 = .475
• Step 3: Look at your z-table and locate the answer from Step 2 in the middle section of the z-table.
• Step 4: In this example, you should have found the number .4750. Look to the far left or the row, you’ll see the number 1.9 and look to the top of the column, you’ll see .06. Add them together to get 1.96. That’s the critical value!
• Tip: The critical value appears twice in the z table because you’re looking for both a left hand and a right hand tail, so don’t forget to add the plus or minus sign! In our example you’d get ±1.96.

Question 76

find a critical value: right-tailed test

Answer 76

• Find a critical value in the z-table for an alpha level of 0.0079.
• Step 1: Draw a diagram, like the one above. Shade in the area in the right tail. This area represents alpha, α. A diagram helps you to visualize what area you are looking for (i.e. if you want an area to the right of the mean or the left of the mean).
• Step 2: Subtract alpha (α) from 0.5: 0.5-0.0079 = 0.4921.
• Step 3: Find the result from step 2 in the center part of the z-table: The closest area to 0.4921 is 0.4922 at z=2.42.

Question 77

find a critical value: left-sided test

Answer 77

• find the critical value in the z-table for α=.012 (left-tailed test).
• Step 1: Draw a diagram, like the one above. Shade in the area in the left tail (because you’re looking for a critical value for a left-tailed test). This area represents alpha, α.
• Step 2: Subtract alpha (α) from 0.5: 0.5 – 0.012 = 0.488.
• Step 3: Find the result from step 2 in the center part of the z-table. The closest area to 0.488 is at z=2.26. If you can’t find the exact area, just find the closest number and read the z value for that number.
• Step 4: Add a negative sign to Step 3 (left-tail critical values are always negative): -2.26.

Question 78

types of critical values

Answer 78

• Various types of critical values are used to calculate significance, including: t scores from student’s t-tests, chi-square, and z-tests. In each of these tests, you’ll have an area where you are able to reject the null hypothesis, and an area where you cannot. The line that separates these two regions is where your critical values are.
• In the above image, the critical values are at 1.28 or -1.28. The blue area is where you must accept the null hypothesis. The red areas are where you can reject the null hypothesis. How large these areas actually are (and what test you use) is dependent on many factors, including your chosen confidence level and your sample size.
• Significance testing is used to figure out if your results differ from the null hypothesis. The null hypothesis is just an accepted fact about the population.

Question 79

what is a t test?

Answer 79

• tells you how significant the differences between groups are, i.e. lets you know if those differences (measured in means/averages) could have happened by chance.
• example: Let’s say you have a cold and you try a naturopathic remedy. Your cold lasts a couple of days. The next time you have a cold, you buy an over-the-counter pharmaceutical and the cold lasts a week. You survey your friends and they all tell you that their colds were of a shorter duration (an average of 3 days) when they took the homeopathic remedy. What you really want to know is, are these results repeatable? A t test can tell you by comparing the means of the two groups and letting you know the probability of those results happening by chance.
  *

Question 80

t score

Answer 80

• ratio between the difference between two groups and the difference within the groups. The larger the t score, the more difference there is between groups. The smaller the t score, the more similarity there is between groups. A t score of 3 means that the groups are three times as different from each other as they are within each other. When you run a t test, the bigger the t-value, the more likely it is that the results are repeatable.

Question 81

types of t test

Answer 81

• An Independent Samples t-test compares the means for two groups.
• A Paired sample t-test compares means from the same group at different times (say, one year apart).
• A One sample t-test tests the mean of a single group against a known mean.
• You probably don’t want to calculate the test by hand (the math can get very messy)

Question 82

paired t test

Answer 82

• A paired t test (also called a correlated pairs t-test, a paired samples t test or dependent samples t test) is where you run a t test on dependent samples. Dependent samples are essentially connected — they are tests on the same person or thing. For example:
  
  • Knee MRI costs at two different hospitals,
  • Two tests on the same person before and after training,
  • Two blood pressure measurements on the same person using different equipment.

Question 83

When to Choose a Paired T Test / Paired Samples T Test / Dependent Samples T Test

Answer 83

• Choose the paired t-test if you have two measurements on the same item, person or thing. You should also choose this test if you have two items that are being measured with a unique condition. For example, you might be measuring car safety performance in Vehicle Research and Testing and subject the cars to a series of crash tests. Although the manufacturers are different, you might be subjecting them to the same conditions.
• With a “regular” two sample t test, you’re comparing the means for two different samples, e.g. you might test two different groups of customer service associates on a business-related test or testing students from two universities on their English skills. If you take a random sample each group separately and they have different conditions, your samples are independent and you should run an independent samples t test (also called between-samples and unpaired-samples).
• The null hypothesis for the for the independent samples t-test is μ1 = μ2. In other words, it assumes the means are equal. With the paired t test, the null hypothesis is that the pairwise difference between the two tests is equal (H0: µd = 0). The difference between the two tests is very subtle; which one you choose is based on your data collection method.

Question 84

One tailed test or two in Hypothesis Testing

Answer 84

• In hypothesis testing, you are asked to decide if a claim is true or not. For example, if someone says “all Floridian’s have a 50% increased chance of melanoma”, it’s up to you to decide if this claim holds merit. One of the first steps is to look up a z-score, and in order to do that, you need to know if it’s a one tailed test or two. You can figure this out in just a couple of steps.
• Example question #1: A government official claims that the dropout rate for local schools is 25%. Last year, 190 out of 603 students dropped out. Is there enough evidence to reject the government official’s claim?
• Example question #2: A government official claims that the dropout rate for local schools is less than 25%. Last year, 190 out of 603 students dropped out. Is there enough evidence to reject the government official’s claim?
• Step 1: Read the question.
• Step 2: Rephrase the claim in the question with an equation. In example question #1, Drop out rate = 25%. In example question #2, Drop out rate < 25%
• Step 3: If step 2 has an equals sign in it, this is a two-tailed test. If it has > or < it is a one-tailed test.

Question 85

t critical value

Answer 85

• A T critical value is a “cut off point” on the t distribution. It’s almost identical to the Z critical value (which cuts off an area on the normal distribution); The only real difference is that the shape of the t distribution is a different shape than the normal distribution, which results in slightly different values for cut off points.
• You’ll use your t value in a hypothesis test to compare against a calculated t score. This helps you to decide if you should support or reject a null hypothesis.

Question 86

how to find a t critical value

Answer 86

• Subtract one from your sample size. This is your df, or degrees of freedom. For example, if the sample size is 8, then your df is 8 – 1 = 7.
• Choose an alpha level. The alpha level is usually given to you in the question — the most common one is 5% (0.05).
• Choose either the one tailed T Distribution table or two tailed T Distribution table. This depends on if you’re running a one tailed test or two.
• Look up the df in the left hand side of the t-distribution table and the alpha level along the top row. Find the intersection of the row and column. For this example (7 df, α = .05,) the t crit value is 1.895.

Question 87

f test

Answer 87

• An “F Test” is a catch-all term for any test that uses the F-distribution. In most cases, when people talk about the F-Test, what they are actually talking about is The F-Test to Compare Two Variances. However, the f-statistic is used in a variety of tests including regression analysis, the Chow test and the Scheffe Test (a post-hoc ANOVA test).
• General steps for an f test: If you’re running an F Test using technology (for example, an F Test two sample for variances in Excel), the only steps you really need to do are Step 1 and 4 (dealing with the null hypothesis). Technology will calculate Steps 2 and 3 for you.
  
  • State the null hypothesis and the alternate hypothesis.
  • Calculate the F value. The F Value is calculated using the formula F = (SSE1 – SSE2 / m) / SSE2 / n-k, where SSE = residual sum of squares, m = number of restrictions and k = number of independent variables.
  • Find the F Statistic (the critical value for this test). The F statistic formula is: F Statistic = variance of the group means / mean of the within group variances. You can find the F Statistic in the F-Table.
  • Support or Reject the Null Hypothesis.

Question 88

F Test to Compare Two Variances

Answer 88

• A Statistical F Test uses an F Statistic to compare two variances, s1 and s2, by dividing them. The result is always a positive number (because variances are always positive). The equation for comparing two variances with the f-test is:
• F = s²₁ / s²₂
• If the variances are equal, the ratio of the variances will equal 1. For example, if you had two data sets with a sample 1 (variance of 10) and a sample 2 (variance of 10), the ratio would be 10/10 = 1.
• You always test that the population variances are equal when running an F Test. In other words, you always assume that the variances are equal to 1. Therefore, your null hypothesis will always be that the variances are equal.
• Assumptions: Several assumptions are made for the test. Your population must be approximately normally distributed (i.e. fit the shape of a bell curve) in order to use the test. Plus, the samples must be independent events. In addition, you’ll want to bear in mind a few important points:
  
  • The larger variance should always go in the numerator (the top number) to force the test into a right-tailed test. Right-tailed tests are easier to calculate.
  • For two-tailed tests, divide alpha by 2 before finding the right critical value.
  • If you are given standard deviations, they must be squared to get the variances.
  • If your degrees of freedom aren’t listed in the F Table, use the larger critical value. This helps to avoid the possibility of Type I errors.

Question 89

how to do f test

Answer 89

• If you are given standard deviations, go to Step 2. If you are given variances to compare, go to Step 3.
• Square both standard deviations to get the variances. For example, if σ1 = 9.6 and σ2 = 10.9, then the variances (s1 and s2) would be 9.62 = 92.16 and 10.92 = 118.81.
• Take the largest variance, and divide it by the smallest variance to get the f-value. For example, if your two variances were s1 = 2.5 and s2 = 9.4, divide 9.4 / 2.5 = 3.76. Why? Placing the largest variance on top will force the F-test into a right tailed test, which is much easier to calculate than a left-tailed test.
• Find your degrees of freedom. Degrees of freedom is your sample size minus 1. As you have two samples (variance 1 and variance 2), you’ll have two degrees of freedom: one for the numerator and one for the denominator.
• Look at the f-value you calculated in Step 3 in the f-table. Note that there are several tables, so you’ll need to locate the right table for your alpha level. Unsure how to read an f-table? Read What is an f-table?.
• Compare your calculated value (Step 3) with the table f-value in Step 5. If the f-table value is smaller than the calculated value, you can reject the null hypothesis.

Question 90

two-tailed f test

Answer 90

• The difference between running a one or two tailed F test is that the alpha level needs to be halved for two tailed F tests.
• With a two tailed F test, you just want to know if the variances are not equal to each other. In notation:
• Ha = σ²₁ ≠ σ²₂
• Sample problem: Conduct a two tailed F Test on the following samples:
  
  • Sample 1: Variance = 109.63, sample size = 41.
  • Sample 2: Variance = 65.99, sample size = 21.
• Step 1: Write your hypothesis statements:
  
  • H_o: No difference in variances.
  • H_a: Difference in variances.
• Step 2: Calculate your F critical value. Put the highest variance as the numerator and the lowest variance as the denominator: F Statistic = variance 1/ variance 2 = 109.63 / 65.99 = 1.66
• Step 3: Calculate the degrees of freedom: The degrees of freedom in the table will be the sample size -1, so:
  
  • Sample 1 has 40 df (the numerator).
  • Sample 2 has 20 df (the denominator).
• Step 4: Choose an alpha level. No alpha was stated in the question, so use 0.05 (the standard “go to” in statistics). This needs to be halved for the two-tailed test, so use 0.025.
• Step 5: Find the critical F Value using the F Table. There are several tables, so make sure you look in the alpha = .025 table. Critical F (40,20) at alpha (0.025) = 2.287.
• Step 6: Compare your calculated value (Step 2) to your table value (Step 5). If your calculated value is higher than the table value, you can reject the null hypothesis:
  
  • F calculated value: 1.66
  • F value from table: 2.287.
  • 1.66 < 2 .287.
  • So we cannot reject the null hypothesis.

Question 91

control variable

Answer 91

A control variable is a regressor included to hold constant factors that, if neglected, could lead the estimated causal effect of interest to suffer from omitted variable bias. The OLS estimator of the effect of interest is unbiased, but the OLS coefficients on control variables are, in general, biased and do not have a causal interpretation.

The reason for including control variables in multiple regression is to make the variables of interest no longer correlated with the error term, once the control variables are held constant.

Question 92

conditional mean independence

Answer 92

• U_i has a conditional mean that does not depend on the X’s given the W’s, that is E(u|X_1i, …, X_ki, W_1i, …, W_ri) = E(u|W_1i, …, W_ri) (conditional mean independence)
• The idea of conditional mean independence is that once you control for the W’s, the X’s can be treated as if they were randomly assigned, in the sense that the conditional mean of the error term no longer depends on X. Controling for W makes the x‘s uncorrelated with the error term so that the OLS can estimate the causal effects on Y of a change in each of the X’s. The control variables however remain correlated to the error term, so the coefficients on the control variables are subject to omitted variable bias and do not have a causal nterpretation.

Question 93

average causal / treatment effect

Answer 93

• ATE = E(Y(1)-Y(0)) with 1 meaning treated and 0 control group; this holds if treatment is binary
  
  • might help: keep in mind that treatment effect is Y(1)-Y(0) - compare to ATE, might be easier to remember then
• if some individuals receive treatment and some do not, the expected difference in observed outcomes between the two goups is E(Y|X=1) - E(Y|X = 0) = E(Y(1)|X=1) - E(Y(0)|X=0); this simply says that the expected difference in the mean treatment outcome for the treated minus the mean no-treatment outcome for the untreated
  
  • with random assignment to treatment and control groups, mean difference ebtween treatment and control group is E(Y|X=1) - E(Y|X = 0) = E(Y(1)|X=1) - E(Y(0)|X=0) = E(Y(1)) - E(Y(0)) = E(Y(1) - Y(0)) where the second eqaulity uses the fact that (Y(1), Y(0)) are independent of X by random assignment; thus, if X is randomly assigned, the mean difference in the experimental outcomes between the two groups is the ATE in the population form which the subjects were drawn
• Although the causal effect cannot be measured for a single individual, in many applications it suffices to know the mean causal effect in a population. For example, a job training program evaluation might trade off the average expenditure per trainee against average trainee success in finding a job. The mean of the individual causal effects in the population under study is called the average causal effect or the average treatment effect.

Question 94

how to estimate the average treatment effect

Answer 94

• can be estimated using an ideal RCE. To see how, first suppose that the subjects are selected at random from the population of interest. Because the subjects are selected by simple random sampling, their potential outcomes, and thus their causal effects, are drawn from the same distribution, so the expected value of the causal effect in the sample is the ATE in the population. Next suppose that subjects are randomly assigned to the treatment or the control group. Because an individual’s treatment status is randomly assigned, it is distributed independently of his or her potential outcomes. Thus the expected value of the outcome for those treated minus the expected value of the outcome for those not treated equals the expected value of the causal effect. Thus, when the concept of potential outcomes is combined with (1) random selection of individuals from a population and (2) random experimental assignment of treatment to those individuals, the expected value of the difference in outcomes between the treatment and control groups is the average causal effect in the population. That is, the ATE on Y_i of treatment (X_i = 1) versus no treatment (X_i = 0) is the difference in the conditional expectations, E(Y_i|X_i = 1) - E(Y_i|X_i = 0), where E(Y_i !X_i = 1) and E(Y_i|X_i = 0) are respectively the expected values of Y for the treatment and control groups in an ideal RCE.

Question 95

probability

Answer 95

of an outcome: proportion of the time that the outcome occurs in the long run

Question 96

sample space

Answer 96

set of all possible outcomes

Question 97

event

Answer 97

• subset of a sample space; that is, an event is a set of one or more outcomes (outcome: mutually exclusive potential result of a random process)
• example: the event “my wireless connection will fail no more than once” is the set consisting of two outcomes: “no failures” and “one failure”

Question 98

random variable

Answer 98

numerical summary of a random outcome, e.g. the numer of times your wireless connection fails while you are writing a term paper is random and takes on a numerical value, so it is a random variable

Question 99

probability distribution

Answer 99

…of a discrete random variable is the list of all possible values of the variable and the probability that each value will occur. These probabilities sum to 1

Question 100

cumulative probability distribution

Answer 100

probability that the random variable is less than or equal to a particular value

Question 101

probability density function

Answer 101

because a continuous random variable can take on a continuum of possible values, the probability distribution used or a discrete variable, which lists the probability of each possible value of the random variable, is not suitable here. Instead, the probability is summarized by the probability density function. The area under this function between any two points is the probability that the random variable falls between those two points

Question 102

expected value of a random variable

Answer 102

• …of a random variable Y, denoted E[Y], is the long-run average of the random variable over many repeated trials or occurences.
• the expected value of a discrete random variable is computed as a weighted average of the posssible outcomes of that random variable, where the weights are the probabilities of that outcome
• also applies to continuous random variables

Question 103

expected value of a Bernoulli random variable

Answer 103

• Bernoulli random variable: binary random variable
• expected value: let G be the Bernoulli random varaible: E(G) = 0x(1-p)+1xp with p being the probability of the binary variable taking on value 1. Thus, the expected value is p, the probability that it takes on the value 1

Question 104

what do variance and sd measure?

Answer 104

the dispersion or the spread of a probability distribution

Question 105

variance of a Bernoulli random variable

Answer 105

the mean of the Bernoulli random variable G is m_G=p, so its variance is (0-p)²*(1-p)+(1-p)²*p = p(1-p)

Question 106

moments of distribution

Answer 106

mean (center of distribution), variance (spread), skewness (lack of symmetry), kurtosis (how thick its tails are)

Question 107

skewness

Answer 107

• E[(Y-m_Y)³]/s³_Y where s is the standard deviation and m the mean
• for a symmetric distribution, a value of Y a given amount above its mean is just as likely as a value of Y the same amount below its mean, thus E=0
• skewness is unit-free
• if a distribution has a long right tail, E>0, and other way round for long left tail

Question 108

kurtosis

Answer 108

• E[(Y-m_Y)²]/s⁴_Y
• measure of how much mass is in its tails and therefore of how much of the variance of Y arises from extreme values. The greater the kurtosis of a distribution, the more likely are outliers
• for a distribution iwth a large amount of amss in its tails, the kurtosis will be large
• kurtosis of a normally distributed variable is 3, so a random variable with kurtosis exceeding 3 has more mass in its tails than a normal random variable
• unit free

Question 109

joint probability distribution

Answer 109

• …of two discrete random variables, say X and Y, is the probability that the random variables simultaneously take on certain values, say x and y. The probabilites of all possible (x,y) combinations sum to 1
• can be written as PR(X=x, Y=y)

Question 110

marginal probability distribution

Answer 110

• …of a raondom variable is just another name for its probability distribution. This term is used to distinguish the distrbution of Y alone (the marginal distribution) from the joint distribution of Y and another random variable
• the marginal distribution of Y can be computed from the join distribution of X and Y by adding up the probabilites of all possible outcomes for which Y takes on a specified value, i.e. Pr(Y=y) = (limits i=1, l) ΣPr(X=xi, Y=y)

Question 111

conditional distribution

Answer 111

distribution of a random variable Y conditional on another random variable X taking on a specific value

Question 112

conditional expectation / mean

Answer 112

mean of the conditional distribution of Y given X. That s, the conditional expectation is the exepcted value of Y, computed using the conditional distribution of Y given X, i.e. E(Y|X=x) = (limits i=1, k)Σy_iPr(Y=y_i|X=x)

Question 114

conditional variance

Answer 114

varaiance of Y conditional on X is the variance of the conditional distribution of Y given X, i.e. var(Y|X=x)=(limits i=1, k)Σ[y_i-E(Y|X=x)]²Pr(Y=y_i|X=x)

example (see table): the conditional variance of the number of failures given htat the computer is old is var(M|A=0)=(0-0.56)²x0.7 + (1-0.56)²x0.13 + (2-0.56)²x0.1 + (3-0.56)²x0.05 + (4-0.56)²x0.02=0.99

Question 115

Bayes’ rule

Answer 115

• the conditional probability of Y given X is the conditional probability of X given Y times the relative marginal probabilities of Y and X: PR(Y=y, X=x) = Pr(X=x|Y=y)Pr(Y=y)/Pr(X=x)
• can be used to deduce conditional probabilities from the reverse conditional probability with the help of marginal probabilities

Question 116

independence

Answer 116

two random variables X and Y are independently distrubuted, or independen,t if knowing the value of one of the variables provides no information about the other. Specifically, X and Y are independent if the conditional distribution of Y given X equals the marginal distribution of Y, i.e if Pr(Y=y|X=x) = Pr(Y=y) OR if Pr(X=x, Y=y) = Pr(x=x)Pr(Y=y), that is, the joint distribution of two independent random variabes is the product of their marginal distributions

Question 117

how to interpret covariance

Answer 117

• reminder: cov(X,Y) = E[(X-m_X)(Y-m_Y)
• suppose that when X is greater than its mean (so that X-m_X is positive), then Y tends to bgerater than its mean (so that Y-m_Y is positive) and that when X is less than its mean, then Y tends to be less than its mean. In both case, the product of the two terms tends to be positive, so the covariance is positive. In contrast, if X and Y tend to move in opposite directions, then the covariance is negative. Finally, if X and Y are independent, the covariance is 0

Question 118

correlation and conditional mean

Answer 118

if the conditional mean of Y does not depend on X, then Y and X are uncorrelated. That is, if E(Y|X)=m_Y, then cov(Y,X) = 0 and corr(Y,X)=0

Question 119

means, variances, and covariances of sums of random variables

Answer 119

Question 120

most common probability distributions

Answer 120

normal, chi-squared, student t, F

Question 121

standard normal distribution

Answer 121

normal distribution with mean m=0 and variance s²=1

Question 122

chi-squared distribution

Answer 122

distribution of the sum of m squred independent standard normal random variables. This distribution depends on m, which is called the degrees of freedom of the distribution, e.g. let Z₁, Z₂, and Z₃ be independent stadnrad normal random variables, then Z²₁ + Z²₂, + Z²₃ has a chi-squred distribution with 3 degrees of freedom

Question 123

student t distribution

Answer 123

• distribution of the ratio of a standard normal random variable to the square root of an independently distributed chi-squared random variable with m degrees of freedom divided by m, i.e. the random variable Z/squareroot (W/m) has a student t distribution iwth m degrees of freedom
• has bell shape similar tothat of the normal distribution, but it has more mass in the tails
• when m≥30m the t distribution is well-approximated by the standard normal distribution and the t(infinity degrees of freedom) equals the standard normal distribution

Question 124

f distribution

Answer 124

with m and n degrees of freedom, is deined to be the distribution of the ratio of a chi-squared random variable with degrees of freedom m, divided by by m, to an independently disributed chi-squared random variable with degrees of freedom n, divided by n, i.e. (W/m)/(V/n) has an F-distribution

Question 125

simple random sampling

Answer 125

• n objects are selected at random from a population (the population of commuting days) and each member of the population (each day) is eqally likely to be included in the sample, i.e. in the example: because the days were selected at random, knowing the value of the commuting time on one of htese randomly selected days provides no information about the commuting time on aother of the days

Question 126

i.i.d draws

Answer 126

becasue the Y’s are randomly drawn from the same popultion the marginal distribution of Y_i, the marginal distribution of Y_i isthe same for each i; thismarginal distribution is the distribution of Y in the population being sampled. When Y_i hasthesame marginal distribution for all i’s, then the Y’s are sad to be identically distributed; when the Y’s are drawn fromthe same distribution and are independently distributed, they are said to be independently and identically distributed

Question 127

law of large numbers

Answer 127

the sample mean will be near the population mean with very high probability when n is large; ths convergence to hte mean is called consistency

Question 128

central limit theorem

Answer 128

the distribution of the sample average is well approxiamted by a normal distribution when n is large

Question 129

Examples of random variables used in this chapter included (a) the sex of the person you meet… Exmaplin why each can be thought of as random

Answer 129

These outcomes are random because they are not known with certainty until they actually occur. You do not know with certainty the gender of the next person you will meet, the time that it will take to commute to school, and so forth.

Question 130

Suppose that the random variables X and Y are independent and you know their distributions. Exaplin why knowing the value of X tells you nothing about the value of Y

Answer 130

If X and Y are independent, then Pr(Y ≤ y | X = x) = Pr(Y ≤ y) for all values of y and x. That is, independence means that the conditional and marginal distributions of Y are identical so that learning the value of X does not change the probability distribution of Y: Knowing the value of X says nothing about the probability that Y will take on different values.

Question 131

Suppose that X denotes the amount of rainfall in your hometown during a randomly selected month and Y denotes the number of children born in L.A. during the same month. Are X and Y independent?

Answer 131

Although there is no apparent causal link between rainfall and the number of children born, rainfall could tell you something about the number of children born. Knowing the amount of monthly rainfall tells you something about the season, and births are seasonal. Thus, knowing rainfall tells you something about the month, which tells you something about the number of children born. Thus, rainfall and the number of children born are not independently distributed.

Question 132

A math class has 100 students, and the mean student weight is 65kg. A random sample of five students is selected from the class, and their average weight is calculated. Will the average weight of the students in the sample equal 65kg? Use this example to explain why the sample average is a random variable.

Answer 132

The average weight of four randomly selected students is unlikely to be exactly 145 lbs. Different groups of four students will have different sample average weights, sometimes greater than 145 lbs. and sometimes less. Because the four students were selected at random, their sample average weight is also random.

Question 133

Suppose that Y’s are i.i.d. random variables with a N(2,6) distribution. Sketch the probability density of th sample avreage when n=2. Repeat this for n=15 and n=200. Describe how the densities differ. What is the relationship between your answers and the law of large numbers?

Answer 133

All of the distributions will have a normal shape and will be centered at 1, the mean of Y. However they will have different spreads because they have different variances. The variance of Y is 4/n, so the variance shrinks as n gets larger. In your plots, the spread of the normal density when n = 2 should be wider than when n = 10, which should be wider than when n = 100. As n gets very large, the variance approaches zero, and the normal density collapses around the mean of Y. That is, the distribution of the sample average becomes highly concentrated around the population average as n grows large (the probability that the sample average is close to the population average tends to 1), which is just what the law of large numbers says.

Question 134

sample variance

Answer 134

(1/(n-1))*(limits i=1, n)Σ(Y_i-Ybar)²

much like the formula for the population variance with two modifications: mu_y is replaced by Ybar, and the average uses the divisor n-1 instead of n. The reason for the first modification is that muy is unknown and thus must be estimated. The reason for the second modification is that estimating muy introduces a small downward bias in (Y_i-Ybar)². This is called a degrees of freedom correction: estimating the mean uses up some of the information - that is, uses up 1 degree of freedom, in the data so that only n-1 degrees of freedom remain

Question 135

standard error of Ybar

Answer 135

is an estimator of the sd of Ybar, i.e. SE(Ybar) = s_Y/squareroot(n). For Bernoulli distribution, SE(Ybar) = squareroot(Ybar(1-Ybar)/n)

Question 136

a statistical hypothesis test can make two types of mistakes

Answer 136

• type I error: null hypothesis is rejected when in fact it is true
• type II error: null hypothesis is not rejected when in fact false

Question 137

testing the hypothesis E(Y) = mu_Y,0 against the alternative E(Y)/= mu_Y,0

Answer 137

1. compute the standard eror of Ybar
2. compute the t-statistic
3. compute the p-value. Reject the hypothesis at the 5% significance level if the p-value is less than 0.05 (equivalently, if |t^act|>1.96)

Question 138

confidence set / level / interval

Answer 138

• confidence set: Because of random sampling error, it is impossible to learn the exact value of the population mean of Y using only the infromation in a sample. However, it is possible to use data from a random sample to construct a set of values that contains the true population mean mu_Y with a certain prespecified priobability, that is, in e.g. 95% of possible samples that might be drawn, the CI will contain the true value of beta1. This is the set of values that cannot be rejected using a two-sided hypothesis test with a x% significance level.
• confidence level: the prespecifided probability that mu_Y is contained in this confidence set
• CI: confidence set for mu_Y is all possible values of the mean between a lower and an upper limit, so that the confidence set is an interval–>CI
• CI calculation: 95% CI = beta1hat - 1.96SE(beta1hat), beta1hat + 1.96SE(beta1hat)

Question 139

hypothesis tests for the difference between two means

Answer 139

• e.g. average compare hourly earnings for men and women; consider the null hypothesis that mean earnings for these two populations differ by a certain amount d₀
• null hypothesis: mu_M - mu_W = d₀ vs H₁: mu_M - mu_W /= d₀
• becuase these popultion means are unknown, they mut be estimated from samples–>Ybar_mYbar_W
• SE(Ybar_M-Ybar_W) = squareroot((s²_m/n_m)+(s²_w/n_w)
• t = ((Ybar_m-Ybar_w)-d₀)/SE(Ybar_m-Ybar_w)

Question 140

causal / treatment effect

Answer 140

difference in the conditional expectations, E(Y|X=x) - E(Y|X=0), where the first term is the expected value of Y for the treatment group, and the latter is the expected value of Y for the control group

Question 141

estimation of the causal effect using differences of means

Answer 141

if the treatment in a RCE is binary, then the causal effect can be estimted by the difference in the sample average outcomes betweenthe treatment and control groups. The hypothesis that the teratment is ineffective is equivalent to the hypothesis that the two means are the same, which can be tested using the t-statistic for comparing two means.

Question 142

A population distribution has a mean of 15 and a variance of 10. Determine the mean and variance of Ybar from an i.i.d. sample form this population for (a) n=5; (b) n=500; (c) n=5000. Relate your answers to the law of large numbers.

Answer 142

In all cases the mean of is 10. The variance of is var(Y)/n, which yields var(Ybar) = 1.6 when n =10, var(Ybar) = 0.16 when n = 100, and var(Ybar) = 0.016 when n =1000. Since var(Ybar) converges to zero as n increases, then, with probability approaching 1, betahat will be close to 10 as n increases. This is what the law of large numbers says.

Question 143

Explain the difference between an unbiased estimator and a consistent estimator.

Answer 143

An estimator is consistent if, as the sample size increases, the estimates (produced by the estimator) “converge” to the true value of the parameter being estimated. To be slightly more precise - consistency means that, as the sample size increases, the sampling distribution of the estimator becomes increasingly concentrated at the true parameter value.

An estimator is unbiased if, on average, it hits the true parameter value. That is, the mean of the sampling distribution of the estimator is equal to the true parameter value.

The two are not equivalent: Unbiasedness is a statement about the expected value of the sampling distribution of the estimator. Consistency is a statement about “where the sampling distribution of the estimator is going” as the sample size increases.

Question 144

standard error vs. standard deviation

Answer 144

Standard Deviation implies a measure of dispersion of the set of values from their mean. Measures how much observations vary from each other.

Standard Error connotes the measure of statistical exactness of an estimate. Measures how precise the sample mean to the true population mean.

Question 145

Why does a CI contain more information than the result of a single hypothesis test?

Answer 145

A confidence interval contains all values of the parameter (for example, the mean) that cannot be rejected when used as a null hypothesis. Thus, it summarizes the results from a very large number of hypothesis tests.

Question 146

regression error term

Answer 146

u_i is the difference between Y_i and its predicted value using the population regression line

Question 147

OLS estimator

Answer 147

• chooses the regression coefficients so htat eh estimated regression line is as close as possible to the observed data, where closenes is emasured by the sum of the squared mistakes made in predicting Y given X
• the sample average, Ybar, is the least squares estimator of the population mean, E(Y); that is, Ybar minimizes the total squared estimation mistakes (limits i=1, n)Σ(Y_i-m)² among all possible estimators m. The OLS estimator extends this idea to the linear regression model: mistake made in predicting Y is Y-(b₀+b₁X). The sum of these squared prediction mistakes over all n observations is the OLS

Question 148

Measures of fit and prediction accuracy: R²

Answer 148

• ranges between 0 and 1 and easures the . fraction of the variance of Y that is explained by X.
• if we write Y as Y_i=Yhat_i + uhat_i In this notation, the R² is the ratio of the sample variance of Yhat to the sample variance of Y
• mathematically, R² can be written as the ratio of the explained sum of square to the total sum of squares. The ESS is the sum of squared deviations of the predictor value Yhat from its average, and the TSS is the sum of squared deviations of Y from its average: ESS = (limits i=1, n)Σ(Yhat-Ybar)² and TSS = (limits i=1, n)Σ(Y-Ybar)²
• R²=ESS/TSS; alternaitvely, R² can be written in terms of the fraction of the variance of Y not explained by X. The sum of squared residuals (SSR) is the sum of the squared OLS residuals: SSR = (limits i=1, n)Σ(uhat)²
• TSS=ESS+SSR–>R²=1-SSR/TSS
• R² of the regression of Y on the single regressor X is the square of the correlation coefficient between Y and X

Question 149

standard eror of the regression (SER)

Answer 149

• estimator of the standard deviation of the regression error u. SER is a measure of the spread of the observations around the regression line.
• SER = s_Uhat=squareroot(s²_Uhat) where s²_Uhat=1/(n-2)Σuhat²=SSR/(n-2)

Question 150

Distinguish between R² and SER. How do each of these measures describe the fit of a regression?

Answer 150

SER is an estimate of the standard deviation of the error term in the regression. The error term summarizes the effect of factors other than X for explaining Y. If the standard deviation of the error term is large, these omitted factors have a large effect on Y. The units of SER are the same as the units of Y. R2 measures the fraction of the variability of Y explained by X, and 1-R2 measures the fraction of the variability of Y explained by the factors comprising the regression’s error term. If R2 is large, most of the variability in Y is explained by X. R2 is “unit free” and takes on values between zero and one.

Question 151

OLS: core assumptions

Answer 151

• error term has a conditional mean of 0 or exogeneity: E(u|X)=0. This means that no matter which value we choose for X, the error term u must not show any systematic pattern and must have a mean of 0.
• random sample: i.i.d. draws; this is often violated when dealing with time series data
• no outliers: all variables have a finite fourth moment
  
  • OLS suffers from sensitivity to outliers.One can show that extreme observations receive heavy weighting in the estimation of the unknown regression coefficients when using OLS. Therefore, outliers can lead to strongly distorted estimates of regression coefficients.

Question 152

how we know that betahat is a consistent estimator of beta if E(u|X)=0

Answer 152

Question 153

endogeneity of x

Answer 153

• variable x is correlated with the error term u, i.e. cov(x,u)/=0
• the OLS estimator is inconsistent if x is endogenous

Question 154

sources of endogeneity

Answer 154

Question 155

counterfactual problem

Answer 155

• counterfactual: what is not, but could have been
  
  • it’s the outcome that would have happened if the treatment was different, e.g. treatment is cholesterol medication: if they receive treatment, we don’t know what their colesterol would have been without treatment
• causality can be defined as the difference between the actual and the counterfactual outcomes
• example: we want to know ATE=E(Y(1))-E(Y(0)), however, we can only observe E(Y(1)|X=1) and E (Y(0)|X=0); in this example, that means we can only observe people that have knowledge of loans and borrow, but not the reverse, so we cannot calculate the treatment effect

Question 156

counterfactual problem solved by OLS?

Answer 156

Question 157

solutions to counterfactual problem

Answer 157

• Two strategies depending on the type of data
• Experimental data
  
  • Units are randomly assigned to either treatment or control group, i.e. x is independent of Y(0), Y(1); hence, E(u|X)=0 holds, thus OLS applies
• Observational data
  
  • Units are as if randomly assigned given some additional assumptions. Assumptions determine which estimation method applies: OLS, IV, Di-in-Di, Fixed Eects

Question 158

internal and external validity of experiments are often criticized due to

Answer 158

• Spillovers/General equilibrium effects
• Not representative sample/context

Question 159

unconditional random assignment

Answer 159

can be conducted by a die, computer - i.e. completely random

Question 160

conditional random assignment

Answer 160

• In some experiments the treatment is randomly assigned conditional on individual characteristics
• OLS with control variable: E(u|X,W)=E(u|W)
• For example, let Y_i be earnings and
  
  • X_i = 1 if individual is assigned to the treatment group that participates in a job training program
  • X_i = 0 if individual is assigned to the control group that does not participate in a job training program
• Suppose that the random assignment is conditional on the level of education where
  
  • 60% of low educated individuals are randomly assigned to the job training program
  • 40% of high educated individuals are randomly assigned to the job training program
• In a regression framework: If we estimate Y_i = β₀ + β₁X_i + u_i, the conditional mean zero assumption (E [u_i|X_i]=0) will be violated.
• The individuals in the control group are on average higher educated than the individuals in the treatment group. High educated individuals generally have higher earnings.
• β₁ will be a biased estimate of the average causal effect of the job training program due to omitted variable bias.
• If we include education as control variable we can obtain an unbiased estimate of the average causal effect of the job training program
• We will however not obtain an unbiased estimate of the effect of education, because education is likely correlated with unobserved characteristics (ability, motivation)

Question 161

testing random assignment

Answer 161

• Random assignment of Xi can sometimes be falsied (tested), but never conrmed
• in experimental data
• in non-experimental data
• In an experiment, however, it is known to the experimenter. Convince others by showing that Xi does not relate to (pre-treatment) covariates Wi
  
  • Regression Xi on Wi
  • Tabulate mean comparison (pre-treatment) covariates Wi
• Randomization cannot be proven because the list of potential (pre-treatment) covariates is endless

Question 162

good control - when are control variables needed?

Answer 162

• Including control variables Wi not needed unless case
  
  • Assignment was random only conditional on Wi, i.e. randomization depends on them, since then E(u|X)=0 does not hold; goal is that given w, x is not correlated with u
    
    • Example: homework conditional on Major status
  • More precision is needed (lower standard errors)
    
    • Including controls reduces the residual variance
  • Best bet: include pre-treatment outcome variable
  • Heterogeneous effects are expected

Question 163

coefficient on control variables interpretation?

Answer 163

coefficient does not have causal interpretation

Question 164

threats to internal validity - experimental (Hawthorne) effects

Answer 164

• In experiments with human subjects, merely because the subjects are in an experiment can change their behavior, a phenomenon sometimes called the Hawthorne effect. In some experiments, a “double-blind” protocol can mitigate the effect of being in an experiment: Although subjects and experimenters both know that they are in an experiment, neither knows whether a subject is in the treatment group or the control group. In a medical drug experiment, for example, sometimes the drug and the placebo can be made to look the same so that neither the medical professional dispensing the drug nor the patient knows whether the administered drug is the real thing or the placebo. If the experiment is double blind, then both the treatment and control groups should experience the same experimental effects, and so different outcomes between the two groups can be attributed to the drug. Double-blind experiments are clearly infeasible in real-world experiments in economics: Both the experimental subject and the instructor know whether the subject is attending the job training program.
• In a poorly designed experiment, this experimental effect could be substantial. E.g. teachers in an experimental program might try especially hard to make the program a success if they think their future employment depends on the outcome of the experiment.
• Both Treated and Controls “behave” differently because they know they are monitored, e.g. in the STAR experiment teachers of small classes might work extra hard bc positive results–>more budgets for small classes

Question 165

threats to internal validity - spillovers

Answer 165

• Treated affect the outcomes of the Controls within the experiment
• Example: Deworming drugs of treated school children in Kenya leads to better outcomes of control students through reduced contamination (Miguel & Kremer, 2004)
• Solution: Conduct an experiment where Treated and Controls are separated far enough
  
  • Spillovers can be identied with an additional treatment
• These threats can lead to violation of conditional mean zero assumption

Question 166

threats to internal validity - failure to randomize

Answer 166

• If the treatment is not assigned randomly, but based in part on characteristics or preferences of the subject, then experimental outcomes will reflect both the effect of the treatment and the effect of the nonrandom assignment.
• E.g. suppose that participants in a job training program experiment are assigned to the treatment group depending on whether their last name falls in the first or second half of the alphabet. Because of ethnic differences in last names, ethnicity could differ systematically between the treatment and control groups. To the extent that work experience, education, and other labor market characteristics differ by ethnicity, there could be systematic differences between the treatment and control groups in these omitted factors that affect outcomes. In general, nonrandom assignment can lead to correlation between X_i and u_i, which in turn leads to bias in the estimator of the treatment effect.
• It is possible to test for randomization. If treatment is randomly received, then X_i will be uncorrelated with observable pretreatment individual characteristics W. Thus, a test for random receipt of treatment entails testing the hypothesis that the coefficients on W_1i,…,W_ri are zero in a regression of X_i on W_1i,…,W_ri, then computing the F-statistic testing whether the coefficients on the W’s are zero, If the experimental design performs randomization conditional on covariates, then those covariates would be included in the regression and the F-test would test the coefficients on the remaining W’s.

Question 167

threats to internal validity - partial compliance

Answer 167

• people do not always do what they are told. In a job training program experiment, for example, some of the subjects assigned to the treatment group might not show up for the training sessions and thus not receive the treatment. Similarly, subjects assigned to the control group might somehow receive the training anyway, perhaps by making a special request to an instructor or administrator.
• In some cases, the experimenter knows whether the treatment was actually received (for example, whether the trainee attended class), and the treatment actually received is recorded as X_i. With partial compliance, there is an element of choice in whether the subject receives the treatment, so X_i will be correlated with u_i even if initially there is random assignment. Thus, failure to follow the treatment protocol leads to bias in the OLS estimator.
• Example: In STAR, some students switched to smaller class (Krueger, 1999)
• Related problem: Substitution. Controls may seek other “treatment”
• If there are data on both treatment actually received (X_i) and on the initial random assignment, then the treatment effect can be estimated by IV regression. IV estimation of the treatment effect entails using the initial random assignment (Z_i) as an instrument for the treatment actually received (X_i).
• Recall that a variable must satisfy the two conditions of instrument relevance and instrument exogeneity to be a valid IV. As long as the protocol is partially followed, then the actual treatment level is partially determined by the assigned treatment level, so the IV Z_i is relevant. If initial assignment is random, then Z_i is distributed independently of u_i (conditional on Wi, if randomization is conditional on covariates), so the instrument is exogenous. Thus, in an experiment with randomly assigned treatment, partial compliance, and data on actual treatment, the original random assignment is a valid IV.
• This IV strategy requires having data on both assigned and received treatment. In some cases, data might not be available on the treatment actually received. For example, if a subject in a medical experiment is provided with the drug but, unbeknownst to the researchers, simply does not take it, then the recorded treatment (“received drug”) is incorrect. Incorrect measurement of the treatment actually received leads to bias in the differences estimator.

Question 168

threats to internal validity - attrition (dropping out)

Answer 168

• refers to subjects dropping out of the study after being randomly assigned to the treatment or control group. Sometimes attrition occurs for reasons unrelated to the treatment program; for example, a participant in a job training study might need to leave town to care for a sick relative. But if the reason for attrition is related to the treatment itself, then the attrition results in bias in the OLS estimator of the causal effect. E.g. suppose that the most able trainees drop out of the job training program experiment because they get out-of-town jobs acquired using the job training skills, so at the end of the experiment only the least able members of the treatment group remain. Then the distribution of unmeasured characteristics (ability) will differ between the control and treatment groups (the treatment enabled the ablest trainees to leave town). In other words, the treatment X_i will be correlated with u_i (which includes ability) for those who remain in the sample at the end of the experiment and the differences estimator will be biased. Because attrition results in a nonrandomly selected sample, attrition that is related to the treatment leads to selection bias.
• Problematic if related to Xi and Yi (related to bad control problem)
• Solution: only by keeping track/give incentives to subjects to stay in sample

Question 169

threats to internal validity - using non-robust standard errors

Answer 169

• this can lead to underestimated standard errors
• null hypothesis rejected too often
• Related problem: Clustering
  
  • within sample correlation between subjects
  • Failure of Key Assumption #2: Random Sample
• Solution: use option robust in stata (or clustering())
• Fraud

Question 170

threats to external validity

Answer 170

• IMPORTANT add-on to internal validity: a threat to internal validity means sth that causes E(u_i|X_i;W_i) /= E (u_i|W_i)
• Non-representative sample
  
  • The population studied and the population of interest must be sufficiently similar to justify generalizing the experimental results. If a job training program is evaluated in an experiment with former prison inmates, then it might be possible to generalize the study results to other former prison inmates. Because a criminal record weighs heavily on the minds of potential employers, however, the results might not generalize to workers who have never committed a crime.
  • Another example of a nonrepresentative sample can arise when the experimental participants are volunteers. Even if the volunteers are randomly assigned to treatment and control groups, these volunteers might be more motivated than the overall population and, for them, the treatment could have a greater effect.
  • More generally, selecting the sample nonrandomly from the population of interest can compromise the ability to generalize the results from the population studied (such as volunteers) to the population of interest.
• Non-representative program/policy:
  
  • The program in a small-scale, tightly monitored experiment could be quite different from the program actually implemented. If the program actually implemented is widely available, then the scaled-up program might not provide the same quality control as the experimental version or might be funded at a lower level; either possibility could result in the full-scale program being less effective than the smaller experimental program. Another difference between an experimental program and an actual program is its duration: The experimental program only lasts for the length of the experiment, whereas the actual program under consideration might be available for longer periods of time.
  • Example: Class Size reduction from 22–>15 says little about 25–>20, which is relevant for policy
• General equilibrium effects: scale and duration of experiment might change economic environment substantially
  
  • Turning a small, temporary experimental program into a widespread, permanent program might change the economic environment sufficiently that the results from the experiment cannot be generalized. A small, experimental job training program, for example, might supplement training by employers, but if the program were made widely available, it could displace employer-provided training, thereby reducing the net benefits of the program. Similarly, a widespread educational reform, such as offering school vouchers or sharply reducing class sizes, could increase the demand for teachers and change the type of person who is attracted to teaching, so the eventual net effect of the widespread reform would reflect these induced changes in school personnel.
  • Phrased in econometric terms, an internally valid small experiment might correctly measure a causal effect, holding constant the market or policy environment, but general equilibrium effects mean that these other factors are not, in fact, held constant when the program is implemented broadly.
  • Returns to schooling will drop if a substantial part of the population attends college
  • When all unemployed follow “interview training” they will compete with each other and not find a job much sooner
• “Black Box” approach (Deaton, 2009; Imbens, 2009)
  
  • Do we learn something fundamental about behavior/mechanisms?

Question 171

What Is the F-test of Overall Significance in Regression Analysis?

Answer 171

• The F-test of the overall significance is a specific form of the F-test. It compares a model with no predictors to the model that you specify. A regression model that contains no predictors is also known as an intercept-only model.
• The hypotheses for the F-test of the overall significance are as follows:
  
  • Null hypothesis: The fit of the intercept-only model and your model are equal.
  • Alternative hypothesis: The fit of the intercept-only model is significantly reduced compared to your model.

Question 172

meaning of adjusted R²

Answer 172

• Similarly to R², adjusted R² also indicates how well terms fit a curve or line, but adjusts for the number of terms in a model. If you add more useless variables to a model, adjusted R² will decrease. If you add more useful variables, adjusted r-squared will increase.
• Adjusted R² will always be less than or equal to R².
• R²_adj = 1-[(1-R²)(n-1)/(n-k-1)]
• Problems with R² that are corrected with an adjusted R²
  
  • R² increases with every predictor added to a model. As R² always increases and never decreases, it can appear to be a better fit with the more terms you add to the model. This can be completely misleading.
  • Similarly, if your model has too many terms and too many high-order polynomials you can run into the problem of over-fitting the data. When you over-fit data, a misleadingly high R² value can lead to misleading projections.

Question 173

interpretation of regression output

Answer 173

• R²: variance in Y explained by regression (i.e. regressors)
• R² adjusted: same as above, but takes into account # of explanatory variables added
• Prob > F: probability against null hypothesis that regression has no explanatory power (by comparing to intercept-only regression): if p<0.01 (0.05 or 0.1), then reject null hypothesis
• coefficients: see different card

Question 174

how to interpret regression coefficients results in e.g. Stata

Answer 174

• Magnitude, i.e. size of the effect, ie. how big the coefficient is. If you increase the balance variable by 1, how much does the Depend1 variable increase by? Be careful here to consider the scale of your variable. If you are using dollars as an independent variable, and you switch to using millions of dollars, the value of your coefficient will drop to a millionth what it was. Did the magnitude of your coefficient change? Not really. We just rescaled. The same is true when you rescale the dependent variable, from employees to millions of employees for example. So given the scaling issue, how do you know when something is important or not? Partly, you make a judgement. If you want a slightly more consistent method in which to make the judgement, ask yourself the following question: If you increase the independent variable by one of its own sds, how much does the dependent variable increase or decrease by? In example: if I increase ‘balance’ by 0.778, how much does this affect Depend1? The predicted effect is an increase of 0.778*0.341 = 0.265. Is 0.265 big? Well, the standard deviation of Depend1 is 0.937. Thus, an increase of one standard deviation in ‘balance’ causes an increase of 0.265/0.937 = 0.283 of a standard deviation in ‘Depend1’.
• Significance, i.e. statistical significance of your estimated coefficient. Do not confuse significance with magnitude. It is more related to the precision of your estimate. Significance is typically measured by your t-statistic, or your p-value in the regression readout. These are the columns ‘t’ and ‘P>|t|’. Typically, a t-statistic above 2 or below -2 is considered significant at the 95% level. We use 2 as a rule of thumb because in the t-distribution we need to know how many degrees of freedom we have (d.f. = number of observations - number of variables) before we can decide whether the value of the t-statistic is significant at the 95% level. If t is very, very large, then we can use the normal distribution, and the t-statistic is significant if it’s above 1.96. If you have few observations in the regression, you might need a slightly higher t-statistic for the coefficient to be significant.

Question 175

testing hypotheses about the slope beta1

Answer 175

• remember that generally, t=(estimator-hypothesized value)/SE of estimator
• first, compute SE of beta1, which is an estimator of the sd of the sampling distribution of beta1; calculating the sd of the estimator is quite complicated, done by software
• second, compute t-statistic
• third, compute p-value; also computed by software

Question 176

mathematical implications of homoskedasticity

Answer 176

• the OLS estimators remain unbiased and asymptotically normal, regardless of homo-/heteroskedasticity
• if least-squares assumptions hold and errors are homoskedastic, then OLS estimators are efficient–>Gauss-Markov theorem

Question 177

homoskedasticity-only vs. heteroskedasticity-robust errors

Answer 177

explore more

Question 178

requirements for IV

Answer 178

• relevance: has some predictive power over endogenous, i.e. correlated with error term (!) x-variable, e.g. children born later in a year may attend school longer
  
  • but relevance first and foremost means that X and W not perfectly collinear
  • it’s testable (F-stat of instruments jointly), first-stage F>10
  • cov(Z,X)/=0 in single variable case, F=t²
• exogeneity: IV and error term should be independent, i.e. corr(z,u)=0
  
  • no correlation with u (independence)
  • no direct effect (exclusion restriction)
• ​For IV regression to be possible, there must be at least as many IV (Z’s) as endogenous regressors (X’s

Question 179

IV explained graphically, mathematically and with example

Answer 179

Question 180

IV general model

Answer 180

Question 181

IV single variable case

Answer 181

Question 182

IV consistency - single variable case

Answer 182

don’t fully understand

Question 183

IV estimation in Stata

Answer 183

check which of the two methods on screenshot work - both? just the 2nd?

Question 184

IV testing Stata

Answer 184

Question 185

IV validity - main problems

Answer 185

• Identication assumption does not hold (exogeneity fails)
  
  • Z related to factors in u (independence fails)
  • Z has direct eect through u (exclusion restriction fails)
  • Unveriable, but can sometimes be assessed by
    
    • test relation with other, pre-determined, W
    • test direct eect through other, post-determined, W
    • checking if results contradict other instrument(s): J−test
• Weak instruments (relevance fails)
  
  • IV can have substantial bias toward OLS when F-stat is small
  • Testable

Question 186

IV definition

Answer 186

• IV is a third variable, Z, used in regression analysis when you have endogenous variables—variables that are influenced by other variables in the model. In other words, you use it to account for unexpected behavior between variables. Using an IV to identify the hidden (unobserved) correlation allows you to see the true correlation between the explanatory variable and response variable, Y.
• Z is correlated with the explanatory variable (X) and uncorrelated with the error term, ε, in the equation: Y = Xβ + ε.
• Let’s say you had two correlated variables that you wanted to regress: X and Y. Their correlation might be described by a third variable Z, which is associated with X in some way. Z is also associated with Y but only through Y’s direct association with X. For example, let’s say you wanted to investigate the link between depression (X) and smoking (Y). Lack of job opportunities (Z) could lead to depression, but it is only associated with smoking through it’s association with depression.

Question 187

IV regression definition

Answer 187

• IV regression splits your explanatory variable into two parts: one part that could be correlated with εand one part that probably isn’t. By isolating the part with no correlation, it’s possible to estimate β in the regression equation: Y_i = β₀ + β₁X_i + ε_i.
• This type of regression can control for threats to internal validity, like:
  
  • Confounding variables,
  • Measurement error,
  • Omitted variable bias
  • simultaneity,
  • Reverse Causality.

Question 188

finding IVs

Answer 188

• you must rely on your knowledge about the model’s structure and the theory behind your experiment (e.g. economic theory). When looking for IVs, keep in mind that Z should be:
  
  • Exogenous —not affected by other variables in the system (i.e. Cov(z,ε) = 0). This can’t be directly tested; you have to use your knowledge of the system to determine if your system has exogenous variables or not.
  • Correlated with X, an endogenous explanatory variable (i.e. Cov(Z,X) ≠ 0). A very significant correlation is called a strong first stage. Weak correlations can lead to misleading estimates for parameters and SEs.

Question 189

IV example - effect of counseling on depression

Answer 189

• want to estimate the effect of a counseling program on depression (measured by rating scale like HAM-D). The relationship between attending counseling and score on the HAM-D may be confounded by various factors. For example, people who attend counseling sessions might care more about improving their health, or they may have a support network encouraging them to go to counseling. The proximity of a patient’s home to the counseling program is a potential instrumental variable.
• However, what if the counseling center is located within a senior community center? Proximity may then cause seniors to spend time socializing or taking up a hobby, which could improve their HAM-D scores. The causal graph in Figure 2 shows that Proximity cannot be used as an IV because it is connected to depression scoring through the path Proximity → Community Center Hours → HAM-D Score.
• However, you can control for Community Center Hours by adding it as a covariate ; If you do that, then Proximity can be used as an IV, since Proximity is separated from HAM-D score, given community center hours.
• Next, suppose that extroverts are more likely to spend time in the community center and are generally happier than introverts. This is shown in the following graph:
• Community center hours is a collider variable; conditioning on it opens up a part-bidirectional path Proximity → Community Center Hours → HAM-D. This means that Proximity can’t be used as an IV.
• As a final step for this example, let’s say you find that community center hours doesn’t affect HAM-D Scores because people who don’t socialize in the community center actually socialize in other places. This is depicted on the following graph:
• If you don’t control for community center hours and remove it as a covariate, then you can use Proximity again as an IV.

Question 190

assessment of QoB as IV for effect of schooling on wage

Answer 190

• exogeneity assessment 1: is Z correlated with u? Yes, QoB related to maternal education, which is also related to wage of child, i.e. there is a correlation of QoB with wages through part of u, here maternal education. This is a violation of independence (See requirements card); in the example, this means ability effects QoB (see attachment)
• exogeneity assessment 2: has Z direct effect through u? yes, since quarter of birth, i.e. being the oldest / youngest in the class, effects attainment / ability, and thus has a direct effect through u; this is a violation of exclusion restriction

Question 191

IV: overidentification J-test

Answer 191

• this is the only way to test for exogeneity (correlation between instrument and error term) of IVs. It only works if the independent variables are overidentified, i.e. more Zs than Xs.
• Suppose that you have a single endogenous regressor and two instruments. Then you could compute two different TSLS estimators: one using the first instrument, the other using the second. These two estimators will not be the same because of sampling variation, but if both instruments are exogenous, then they will tend to be close to each other. If these two instruments produce very different estimates you might conclude that there is something wrong with one or the other of the instruments, or both. That is, it would be reasonable to conclude that one or the other, or both, of the instruments are not exogenous.
• in attachment, 2 means that all Zs are exogenous
• Interpretation:
  
  • Rejection of J-test means instruments contradict, i.e. give signicantly different slope estimates betahat
  • Reasons for contradiction
    
    • One or more instruments are invalid (which one unknown)
    • Effect is heterogeneous [next] or non-linear [not discussed]
  • Also, failure to reject doesn’t mean exogeneity holds (unveriable), but may sometimes give additional comfort
    
    • All wrong, but not contradict; low power
  • Therefore, J-test outcomes should be interpreted with care

Question 192

a rule of thumb for checking weak instruments

Answer 192

• in the case of a single endogenous regressor X one may use the following rule of thumb: Compute the F-statistic which corresponds to the hypothesis that the coefficients on Z₁,…,Z_m are all zero in the first-stage regression. If the F-statistic is less than 10, the instruments are weak such that the TSLS estimate of the coefficient on X is biased and no valid statistical inference about its true value can be made.
• There are two ways to proceed if instruments are weak:
  
  • Discard the weak instruments and/or find stronger instruments. The former is only an option if the unknown coefficients remain identified when the weak instruments are discarded.
  • Stick with the weak instruments but use methods that improve upon TSLS in this scenario, for example limited information maximum likelihood estimation, see Appendix 12.5 of the book.
• As rule of thumb only conduct IV if F > 10, because then the IV bias is approximately less than 10% that of OLS, and SE’s and t-tests are approximately correct

Question 193

heterogeneity

Answer 193

• Students, people, rms, counties, observational units i in general have dierent effects, beta:
  
  • Smart kids do not prot from compulsory homework, while others do
  • Rich people insensitive to taxes on cigarettes
  • Teachers respond less to incentive schemes than bankers
• Heterogeneity with respect to observable W_1i can be identied and tested. Include interaction W_1i x Xi (and main effect W_1i)

Question 194

OLS with heterogeneous causal effects

Answer 194

Question 195

IV regression with heterogeneous causal effects

Answer 195

• important: here the heterogeneity is not in the effect on Y of X, but on X of Z, so here the coefficient pi₁ varies from one individual to the next, not beta₁.
• continuation from attachment: …weight on those individuals (more generally, entities) whose treatment probability is most influenced by the instrumental variable.

Question 196

local average treatment effect

Answer 196

• It is the treatment effect for the subset of the sample that takes the treatment if and only if they were assigned to the treatment, otherwise known as the compliers. It is not to be confused with the average treatment effect (ATE), which is the average subject-level treatment effect; the LATE is only the ATE among the compliers. The LATE can be estimated by a ratio of the estimated intent-to-treat effect and the estimated proportion of compliers, or alternatively through an instrumental variable estimator.
• Sometimes a treatment or a program is delivered but for some reason or another only some individuals or groups actually take the treatment. In this case it can be hard to estimate treatment effects for the whole population. For example maybe people for whom the treatment would have had a big effect decided not to take up the treatment. In these cases it is still possible to estimate what’s called the “Local Average Treatment Effect,” or LATE. This guide1 discusses the LATE: what it is, how to estimate it, and how to interpret it.2
• Noncompliance can make it impossible to estimate the average treatment effect (ATE) for the population. For example, say that in a population of 200, 100 people are randomly assigned to treatment and we find that only 80 people are actually treated. What is the impact of the treatment? One method to answer this question is simply to ignore the noncompliance and compare the outcome in the treatment (100 people) and control (100 people) groups. This method estimates the average intention-to-treat effect (ITT). While informative, this method does not give a measure of the effect of the treatment itself. Another approach would be to compare the 120 really-untreated and 80 really-treated subjects. Doing so, however, might give you biased estimates. The reason is that the 20 subjects that did not comply with their assignment are likely to be a nonrandom subset of those that were assigned to treatment. Solution is LATE
• Before we can calculate the LATE under one-sided noncompliance we need to make an assumption. The exclusion restriction (also called “excludability”) stipulates that outcomes respond to treatments, not treatment assignments. In normal words this simply means that the outcome for a Never-Taker is the same regardless of whether they are assigned to the treatment or control group: in both cases the subject is not treated, and that is what matters.

Because the treatment was randomly assigned, we know that if there are 20% Never-Takers in the treatment group (left column), there are probably about 20% Never-Takers in the control group. Because of the exclusion restriction, the Never-Takers have the same outcome under both assignment conditions, and thus the difference in average outcomes (40) cannot be attributed to the Never-Takers. We can thus attribute the entire ITT effect to the Compliers. The LATE can therefore be estimated by dividing the ITT estimate by the share of Compliers: 40/0.8 = 50.

Question 197

three conclusions w.r.t the multiple regression model with control variables

Answer 197

1. OLS provides unbiased estimators for the x-coefficients (betas) and the w-coefficients(deltas) and the OLS estimators are consistent and have a normal distribution in large samples
2. under the conditional mean independence assumption(E(u|X,W)=E(u|W)=gamma₀ + gamma₁W₁+…+gamma_kW_k), the OLSestimators of the coefficients on the X’s have a ausal interpretation, i..e they are unbiased for the causal effects beta₁…
3. the coefficients on the control variables do not, in general, have a causal interpretation. The reason is that those coefficients estimate any direct causal effect of the control variables, plus a term (the gammas) arising becuase of correlation between u and the control variable. Thus, under conditional mean independence, the OLS estimator of the coefficients on the control variables, in general, suffer from ommitted variable bias

Question 198

why IV is needed?

Answer 198

• Problem: y = a+bx+e: X and error term are correlated, meaning that if x changes, there are two ways in which y is changing: one is due to x, the other due to the factors contained within the error term. The equation clearly shows that any OLS estimate of beta will not be equal to the original beta
• So how do IVs solve this issue? If we can find a third variable that is correlated with x but uncorrelated with e, then if z changes, this causes x to change which causes y to change, but the only reason why y is changing is due to the change in x
• side note: could include omitted variable in regression instead of IV to solve this issue, but that does only feasible if you have data on it
• the picture shows that LS is inconsistent, so this shows: how does the IV estimator compare to the least squares estimator?
  
  • Bias: LS and IV estimator are biased, so no improvement of IV over LS here
  • Consistency: LS estimator is inconsistent, IV estimator is consistent

Question 199

how to derive the explicit form of the IV estimator of a bivariate model

Answer 199

Question 200

which of the three characteristics of an estimator is violated by endogeneity: unbiasedness, consistency or efficiency?

Answer 200

• unbiasedness: the expected value of the OLS estimator /= beta; this is because if endogeneity, then x correlated with error term. This means that if x increases, y increases, but error term increases too, which in turn increases y even more, so biased
• consistency: as n tends toward infinity, OLS estimator does not tend toward beta

Question 201

how two-stage IV regression works

Answer 201

• The first stage decomposes X into two components: a problematic component that may be correlated with the regression error and a problem-free component that is uncorrelated with the error. The second stage uses the problem-free component to estimate b₁.
• The first stage begins with a population regression linking X and Z (see attachment) where p₀ is the intercept, p₁ is the slope, and vi is the error term. This regression provides the needed decomposition of X_i. One component is p₀ + p₁Z_i, the part of X_i that can be predicted by Z_i. Because Z_i is exogenous, this component of X_i is uncorrelated with u_i, the error term in Equation (12.1). The other component of X_i is v_i, which is the problematic component of X_i that is correlated with u_i.
• The idea behind TSLS is to use the problem-free component of X_i, p₀ + p₁Z_i, and to disregard v_i. The only complication is that the values of p₀ and p₁ are unknown, so p₀ + p₁Z_i cannot be calculated. Accordingly, the first stage of TSLS applies OLS to Equation (12.2) and uses the predicted value from the OLS regression, Xhat = phat₀ + phat₁Z_i, where p₀ and p₁ are the OLS estimates.
• The second stage of TSLS is easy: Regress Y_i on Xhat using OLS. The resulting estimators from the second-stage regression are the TSLS estimators, betahat₀^TSLS and betahat₁^TSLS.

Question 202

how to show that bhat₁^TSLS is consistent

Answer 202

Question 203

IV regression with multiple regressors

Answer 203

• When there are multiple endogenous regressors X_1i,…, X_ki, the TSLS algorithm is similar, except that each endogenous regressor requires its own first-stage regression: the dependent variable is one of the X’s, and the regressors are all the instruments (Z’s) and all the included exogenous variables (W’s). Together, these first-stage regressions produce predicted values of each of the endogenous regressors.

Question 204

why can we use general procedures for statistical inference form regression models for TSLS regression as well (hypothesis tests and CIs)

Answer 204

• Because the sampling distribution of the TSLS estimator is normal in large samples. For example, 95% CIs are constructed as the TSLS estimator {1.96} standard errors. Similarly, joint hypotheses about the population values of the coefficients can be tested using the F-statistic.

Question 205

TSLS SEs

Answer 205

• Two points to bear in mind about TSLS SEs.
  
  • First, the SEs reported by OLS estimation of the second-stage regression are incorrect because they do not recognize that it is the second stage of a two-stage process. Specifically, the second-stage OLS SEs fail to adjust for the second-stage regression using the predicted values of the included endogenous variables. Formulas for SEs that make the necessary adjustment are incorporated into (and automatically used by) TSLS regression commands in econometric software.
    
    • Second, as always the error u might be heteroskedastic. It is therefore important to use heteroskedasticity-robust versions of the SEs for precisely the same reason as it is important to use heteroskedasticity-robust standard errors for the OLS estimators of the multiple regression model.

Question 206

IV: application to demand for cigarettes example

Answer 206

• In this analysis, we focus on estimating the long-run price elasticity. We do this by considering quantity and price changes that occur over 10-year periods. Specifically, in the regressions considered here, the 10-year change in log quantity, ln(Q^cigarettes_i,1995) - ln(Q^cigarettes_i,1985), is regressed against the 10-year change in log price, ln(P^cigarettes_i,1995) - ln(P^cigarettes_i,1985), and the 10-year change in log income, ln(Inc_i,1995) - ln(Inc_i,1985). Two instruments are used: the change in the sales tax over 10 years, SalesTax_i,1995 - SalesTax_i,1985, and the change in the cigarette-specific tax over 10 years, CigTax_i,1995 - CigTax_i,1985.
• The only difference between the three regressions is the set of IVs used. In column (1), the only instrument is the sales tax; in column (2), the only instrument is the cigarette-specific tax; and in column (3), both taxes are used as instruments.
• In IV regression, the reliability of the coefficient estimates hinges on the validity of the instruments, so the first things to look at in Table 12.1 are the diagnostic statistics assessing the validity of the instruments.
  
  • IVs relevant? look at the first-stage F-statistics. The first-stage regression in column (1) is [attachment 2] Because there is only one instrument in this regression, the first-stage F-statistic is the square of the t-statistic testing that the coefficient on the IV, SalesTax_i,1995 - SalesTax_i,1985, is zero; this is F = t² = (0.0255/0.0044)² = 33.7. For the regressions in columns (2) and (3), the first-stage F-statistics are 107.2 and 88.6, so in all three cases the first-stage F-statistics exceed 10 –> IVs not weak, so we can rely on the standard methods for statistical inference (hypothesis tests, confidence intervals) using the TSLS coefficients and SEs.
  • IVs exogenous? Because the regressions in columns (1) and (2) each have a single IV and a single included endogenous regressor, the coefficients in those regressions are exactly identified. Thus we cannot deploy the J-test in either of those regressions. The regression in column (3), however, is overidentified because there are two IVs and a single included endogenous regressor, so there is one (m - k = 2 - 1 = 1) overidentifying restriction. The J-statistic is 4.93; this has a x₂₁ distribution, so the 5% critical value is 3.84 and the null hypothesis that both the instruments are exogenous is rejected at the 5% significance level (this deduction also can be made directly from the p-value of 0.026, reported in the table). The reason the J-statistic rejects the null hypothesis that both instruments are exogenous is that the two instruments produce rather different estimated coefficients. Recall the basic idea of the J-statistic: If both instruments are exogenous, then the two TSLS estimators using the individual instruments are consistent and differ from each other only because of random sampling variation.
• The J-statistic rejection means that the regression in column (3) is based on invalid instruments (the instrument exogeneity condition fails). What does this imply about the estimates in columns (1) and (2)? The J-statistic rejection says that at least one of the instruments is endogenous, so there are three logical possibilities: The sales tax is exogenous but the cigarette-specific tax is not, in which case the column (1) regression is reliable; the cigarette-specific tax is exogenous but the sales tax is not, so the column (2) regression is reliable; or neither tax is exogenous, so neither regression is reliable. The statistical evidence cannot tell us which possibility is correct, so we must use our judgment.

Question 207

what do estimatoers estimate if there is population heterogeneity?

Answer 207

When X is as-if randomly determined, the OLS estimator is a consistent estimator of the ATE. That is generally not true for the IV estimator, however. Instead, if X is partially influenced by Z,then the IV estimator using the instrument Z estiamtes a weighted average of the causal effects, where those for whom the instrument is most influential receive the most weight.

Question 208

OLS with heterogeneous causal effects

Answer 208

Question 209

three cases in which LATE = ATE

Answer 209

Question 210

example for when LATE and ATE differ

Answer 210

• implications:
• If an individual’s decision to receive treatment depends on the effectiveness of the treatment for that individual, then the TSLS estimator in general is not a consistent estimator of the ATE. Instead, TSLS estimates a LATE, where the causal effects of the individuals who are most influenced by the instrument receive the greatest weight.
• This conclusion leads to a disconcerting situation in which two researchers, armed with different instrumental variables that are both valid in the sense that both are relevant and exogenous, would obtain different estimates of “the” causal effect, even in large samples. The difference arises because each researcher is implicitly estimating a different weighted average of the individual causal effects in the population. In fact, a J-test of overidentifying restrictions can reject if the two instruments estimate different local average treatment effects, even if both instruments are valid. Although both estimators provide some insight into the distribution of the causal effects via their respective weighted averages, in general neither estimator is a consistent estimator of the ATE.

Question 211

another example for when LATE and ATE differ

Answer 211

Question 212

advantages of panel data

Answer 212

• More control over omitted variables
• More observations
• Many research questions typically involve a time component

Question 213

panel data with more than two time periods

Answer 213

important to remember: a_i is the state-specific intercept, i.e. graphically, it’s the y-axis intercept, so for US states they would have different intercepts, but the same slope

Question 214

Fixed effect estimation using within transformation

Answer 214

Question 215

Fixed effects distribution and testing

Answer 215

• normal distribution, so can “normal” t-test and F-test
• T-test in STATA:

xtset state year

xtreg Y X, fe cluster(state)

test X=0

Question 216

when use time fixed effects?

Answer 216

• Needed when common changes (the trend) in u, coincides with the common changes (the trend) in X e.g. taxes go up as economy grows, and so does traffic (this is from example regression of beer taxes on traffic fatalities)
• Time effects control for the trend that is common to all entities (states)
• With T = 2 periods and (potentially) dierent units i per time period this is the Dierences-in-Dierences model

Question 217

panel data limitations - X’s that do not change

Answer 217

Question 218

panel data limitations - simultaneity / reversed causality

Answer 218

Question 219

how to estimate causal effects in quasi-experiments

Answer 219

• if whether an individual receives treatment is viewed as if it is randomly determined–>can be estimated by OLS using the treatment, X as a regressor
• if the as-if variation only partially determines the treatment–>estimate using IV regression, where the as-if random source of variation provides the IV

Question 220

[just interesting] does immigration reduce wages?

Answer 220

• Economic theory suggests that the increase in labor supply would drive down wages. However, all else being equal, immigrants are attracted to cities with high labor demand, so the OLS estimator of the effects on wages of immigration will be biased (bc through this behavior, immigration is not independent of the error term, i.e. correlated with other stuff that impacts Y).
• Am ideal randomized controlled experiment for estimating the effect on wages of immigration would randomly assign different numbers of immigrants (different “treatments”) tp different labor markets (“subjects”) and measure the effect on wages (“outcome”). Such an experiment, however, faces severe practial, financial and ethical problems.

Question 221

why use DiD estimator? / DiD definition

Answer 221

• Since in a quasi-experiment the researcher does not have control over the randomization, some differences might remain between the treatment and control groups even after controlling for W. One way to adjust for those remaining differences between the two groups is to compare not the outcomes Y but the change in the outcomes pre- and posttreatment, threby adjusting for the differences in pretreatment values of Y in the two groups.
• Since this estmator is the difference across groups in the change, or difference over time, it is called the DiD estimator
• DiD is the average change in Y for those in the treatment group minus the average change in Y for those in the control group
• if the treatment is drandomly assigned, then the estimator is an unbiased and consistent estimator of the causal effect. By focusing on the change in Y over the course of the experiment the DiD estimator removes the influence of initial values of Y that vary between the treatment and control groups

Question 222

repeated cross-sectional data set

Answer 222

• collection of cross-sectional data sets, where each data set corresponds to a different time period. Example: political poling data, inw which political preferences are emasured by a series of surveys of randomly selected potential voters, where the surveys re taken at different dates and each survey has different respondents.
• The premise of using this method is that if the individuals are randomly drawn from the same population, then the individuals in the earlier cross section can be used as surrogates for the individuals in the treatment and cntrol groups in the later cross section

Question 223

IV estimators in quasi-experiments

Answer 223

If the quasi-experiment yields a variable Z_i that influences receipt of treatment, if data are available both on Z_i and on the treatment actually received (X_i ), and if Z_i is “as if” randomly assigned (perhaps after controlling for some additional variables W_i), then Z_i is a valid instrument for X_i.

Question 224

why do control variables w have no causal interpretation?

Answer 224

they remain correlated with the error term, (E(u|x,w)=E(u|w) so the coefficients on the control variables are subject to OVB and do not have a causal interpretation.

Question 225

IV reduced form

Answer 225

regression of Z on Y, i.e. IV on outcome