Macro - Week 1 Flashcards
The Ramsey-Cass-Koopmans model (base model), micro-foundations of macro-models, equilibrium definition, planner’s problem, welfare, Euler equation, phase-diagram.
1
Q
RCK model: Components and simplifications
A
- Components
- The economy consists of a large number of identical, price taking firms and a large number of identical price taking infinitely lived households
- Profit maximising firms choose production factors K and L
- Utility maximising consumers choose C, always work full-time
- Simplifications compared to the book
- No population growth; population standardised to L = 1
- One person household, H = 1
- No technological growth, technology standardised to A = 1
- Discrete time, so summation instead of integration
- Log utility instead of CRRA, U(C) = ln(C)
- But… non-zero depreciation
2
Q
Firms in RCK model
A
- Production determined by a constant returns to scale production technology with diminishing returns to each production factor
- Their capital stock depreciates at rate δ and grows with investments
- Present value of future and current profits

3
Q
Firms: FOCs
A
- Capital demand
- Firms face a trade-off: using more capital costs interest rate plus discount rate (marginal cost of capital). The benefits are the marginal productivity of capital
- Profit maximisation implies that marginal costs equal marginal benefits
- If the marginal product of capital exceeds the costs, firms want to invest more, (potentially) increasing the interest rate and lowering the marginal productivity of capital
Labour demand
- Marginal cost of labour (the wage) equals the marginal productivity of labour
- If the marginal product of labour exceeds the costs, firms hire more labour, which lowers marginal productivity and (potentially) increases wages

4
Q
Consumers: Optimization
A
Consumers maximise present value of utility given current assets, current and future income and interest rates. Labour supply is inelastic and standardised to one (Lt = 1). The only savings possibility is capital, which generates a return of rt. For log-utility we have
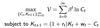
5
Q
Consumers: Solution 1
A

6
Q
Consumers: Solution 2
A

8
Q
The full RCK model
A
- A “minor” problem
- Given K0, At, Gt these six equations determine Yt, wt, rt, Kt+1, Lt, and Ct.
- Unfortunately, an explicit solution is very hard to find
- Solutions
- Graphical analysis (phase diagram, only qualitative answers)
- Special case(s)
- Approximate (log-linearise) general solution
- Approximate using computer (e.g. Matlab - Dynare)

10
Q
Graphical analysis (phase diagram)
A
- Core model: two dynamic equations
- Drop Lt (= 1), simplify and the dynamics of this system are given by the Euler equation and the capital accumulation equation

11
Q
Phase diagram: consumption
A

12
Q
Phase diagram: capital stock
A

13
Q
Phase diagram: dynamics
A
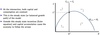
14
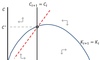
Q
Phase diagram: saddle path
A
15
Q
Social planner
A
- This planner maximises welfare (which is utility of the representative household in this simple model)
- Has to obey the forces of nature (capital accumulation) and market clearing
- But may ignore factor prices and other incentives
- Solution - solving the social planner’s problem gives (see 2nd attachment)
- same as the market equilibrium!
- Punchline: In this simple model, the market equilibrium is exactly the same as the welfare maximising equilibrium! There is no role for government intervention! This result turns out to be more general (under perfect competition, finite number of agents and
products)

16
Q
RCK model: equilibrium
A
- Labour market
- Everybody supplies one unit of labour. Standardise mass of people to one. Lt = 1
- Goods market
- Production is used for consumption, investment and government consumption: Yt = Ct + It + Gt
- Combined with capital accumulation identity: Kt+1 = (1 − δ)Kt + Yt − Ct − Gt
- Capital market equilibrium already imposed (and it clears by Walras’ law)
18
Q
A
19
Q
theta in CRRA
A
- U(C(t)) = C(t)1-theta/1theta - this is known as constant-relative-risk-aversion (CRRA)
- theta is the coefficient of relative risk aversion. Since there is no uncertainty in this model, the household’s attitude s not directly relevant. But theta also determines the household’s willingness to shift consumption between different periods. When theta is smaller, MU falls more slowly as C rises, and so the household is more willing to allow its consumption to vary over time. If theta is closeto zero, e.g., utility is almost linear in C (see equation above!), and tso the household is willing to accept large swings in C to take advantage of small differences between the discount rate and the rate of return on saving.


