Optimisation

Question 1

Define the concept of variable lifetime

Answer 1

A variable is alive from the moment it is first defined to when that write is read from for the last time..

Question 2

Describe Unconstrained Left Edge Algorithm

Answer 2

This is a method of mapping variables to registers.

Required as registers if ideal form of memory, however, likely more registers than variables.

Question 3

What happens when a variable escapes?

Answer 3

Means value must be stored in memory as registers are full.

Question 4

Steps for unconstrained left edge algorithm

Answer 4

1. Mark all variable segments unmapped to registers.
2. Select an empty register.
3. Take the next unmapped segment whose left edge
   is to the right of the left edge of the last segment
   mapped on that register (sorry).
4. Map that segment to that register.
5. If there are more variable segments and more
   registers, go to 2.

Question 5

Describe Tree height reduction

Answer 5

Reduce the “height” of an expression tree, so the
“parallel sections” can be put through separate
pipelines.
Example: x = a + b + c + d:

Question 6

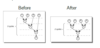
Describe constant folding

Answer 6

Rearrange expressions to minimise evaluation cost at
runtime. Effective when used with inline functions
with constants.

Question 7

Describe Constant Propagation

Answer 7

Constant propagation is the process of substituting the values of known constants in expressions. Constant propagation eliminates cases in which values are copied from one location or variable to another, in order to simply assign their value to another variable.

Question 8

Describe variable propagation

Answer 8

Can be used to completely eliminate a variable.

Question 9

Describe Sub Expression Elimination

Answer 9

Eliminate repeated evaluation of expressions whose
value does not change. Often creates a temporary
variable (which often ends up stored in a register for
the duration of its use).

Question 10

Describe Dead Code Elimination

Answer 10

Remove code that is unreachable/ not reached.

Question 11

Describe Operator Strength Reduction

Answer 11

Replace operators with cheaper/faster operators that
produce identical results:
a = x * 3
Split the multiply. . .
a = x * 2 + x
Doubling is better as a shift. . .
a = ( x<<1) + x
A common case of this is b=x^2 ! b=x*x.

Question 12

Describe algebraic identity recognition

Answer 12

• a + 0 = a
• a - 0 = a
• a X 1 =a
• a / 1 = a
• XOR(a; a) = 0

Replacement of algebra with result to avoid redundant calculation

Question 13

Describe Pre-emptive Evaluation

Answer 13

Consider:
b o o l a , b ;
a = e x p e n s i v e o p e r a t i o n o n e ( ) ;
i f ( a ) e x p e n s i v e o p e r a t i o n two ( ) ;

We can start evaluating expensive_operation_two
at the same time as expensive_operation_one
(assuming no data ow issues). Simply throw away
the result if it’s not needed.

Question 14

Describe Procedural Inlining

Answer 14

Replace a function call with its body. Given
int add ( int a, int b ){ return a + b ; }
…
int a , b , c ;
a = 2 ;
b = 4 ;
Then “c = add(a, b);” becomes “c = a + b;”.
Difficult to automate, but \activates” many data ow
transformations

Question 15

Describe Conditional Expansion

Answer 15

Replaces control flow instructions with other
instructions:
boo l a;
if ( a ) {x = b + d ; }
else {y = p + q; }
becomes:
bool a ;
x = a ( b + d ) + a ` x ;
y = ay + a ` ( p + q ) ;

Requires intimate knowledge of the instruction set.

Question 16

Describe Loop Unwinding

Answer 16

Expand iterative loops with a fixed number of
iterations (in whole or in part):
int i , x ; x = 0 ;
for ( i =1; i <4; i++) x = x + i ;
becomes:
int x = 0 ;
x = x + 1 ;
x = x + 2 ;
x = x + 3 ;
Works best if the loop contents are small.

Question 17

Describe Loop Fusion

Answer 17

Merges two or more loops into one (which may then
be unwound).
• Only one control variable, and one termination check.

• For loops of different ranges, conditionals are used to “ignore” unwanted iterations.
• A “remainder loop” may be created.

Question 18

Describe Loop Invariance

Answer 18

Move “unchanging” code from inside a loop to the
outside:

int a , i , x ; x = 0 ;
f o r ( i =1; i <4; i++)
{
a = 3 ;
x = x + a ;
}
becomes:
int i , x ; x = 0 ; a = 3 ;
for ( i = 1; I < 4; i++) x = x + a ;

Question 19

Describe Loop Switching

Answer 19

Moving of if statements outside of the loop

Question 20

What are we optimising for?

Answer 20

• Memory footprint
• Execution time