Norms 1 - 4 Flashcards
Define a norm on a vector space X
Define the standard euclidean norm in Rn
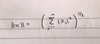
Define a normed space
A pair (X, || . ||) where || . || is a norm and X is a vector space
Define convex on a vector space
Define the closed unit ball BX and prove that it’s convex in a normed space
Define convex on a function f:[a,b] to R
Define the lp norms
State and prove Minkowski’s inequality in Rn
When are two norms equivalent
Define the lp sequence space
What do we denote by C[(a,b)]?
the space of real-valued continuous functions on the interval [a,b]
What norm do we use normally on C( [a,b] )
Define a metric d on a set X
Define the discrete metric on X
d(x,x) = 0 and d(x,y) = 1 if x isnt equal to y
Define the open ball B(a,r) and the closed ball
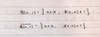
When is a subset S of (X,d) bounded
if there exist a in X and r > 0 such that S is a subset of B(a, r)
Show that if A is a bounded subset of (X,d) there is an a in A and r > 0 such that A is a subset of B(a, r)
Define open and closed for a subset U of (X,d)
Lemma: Open balls are open
Lemma: If U1, ……., Un are open then the intersection is open
Lemma: If U1,……, Un are open then the union is open
When does a sequence (xn) converge to some x in X
Lemma: A sequence can have at most one limit
Lemma: A subset of a metric space is open if and only if it’s the union of open balls
Define continuity for a function f: X to Y on metric spaces
Lemma: Suppose that X,Y,Z are metric spaces and f: X to Y, g: Y to Z are continuous. Then gf: X to Z is continuous
If U is an open subset of Z then g-1(U) is open in Y. So f-1(g-1(U)) is open in X
The functions f(x,y) = y and g(x,y) = x - 7y are continuous, so U = f-1(0, inf) intersect g-1(0, inf) is open
When are two metrics topologically equivalent
Two metrics d1 and d2 are called topologically equivalent if the open sets (X, d1) and (X, d2) coincide
When is f: X to Y an isometry between X and Y
When dy(f(x), f(y)) = dx(x,y)
When is f: X to Y a homeomorphism?
If f is a bijection such that f and f-1 are continuous. U is open in X if and only if f(U) is open in Y
Define a topological property of a metric space (X,d)
A topological property is a property such that every metric space homeomorphic to (X,d) has the same property
Give 4 examples of topological properties
- X is open, X is closed
- X is finite, countable, uncountable
- every subset of X is open
- every continuous real valued function on X is bounded
