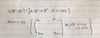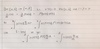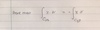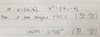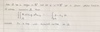Multivariable Calculus Flashcards
(100 cards)
1
Q
Define Euclidean distance for x,y in Rn
A
2
Q
Define the Euclidean norm
A
3
Q
Define the | . |1 norm
A
4
Q
Define convergence for a sequence of vectors (xj)
A
5
Q
Define the scalar product
A
6
Q
State and prove the Cauchy-Schwartz inequality
A
7
Q
Define cos theta with regards to the cauchy schwartz inequality
A
8
Q
State and prove the triangle inequality
A
9
Q
State the relationship between the euclidean norm and the 1 norm
A
|x| <= |x|1 <= sqrt(n) |x|
10
Q
Define the infinity norm
A
11
Q
State and prove the relationship between the euclidean norm and the infinity norm
A
12
Q
Prove the uniqueness of limits for a sequence (xj)
A
13
Q
A
14
Q
A
15
Q
A
16
Q
A
17
Q
Give the sequential definition of continuity
A
f is continuous at p, if for every sequence (xj) which converges to p, f(xj) converges to f(p)
18
Q
A
19
Q
A
20
Q
A
21
Q
A
22
Q
Prove that a Cauchy sequence (xj) is convergent
A
23
Q
Define the Open Ball
A
24
Q
Define continuity of a function f: U to Rn at p in terms of open balls
A
25
When is U, a subset of Rn, open?
26
27
Define the epsilon nieghbourhood of E
28
Proposition: If E1,......., Em are all closed then the union is closed
29
Proposition: Let U1,......,Um be open sets, then the intersection is open
30
Proposition: A set is closed if and only if it contains all its limit points
31
Define relatively open
32
Define an isolated point of U
33
Define a continuous limit
34
35
Define a path from p in Rn to q in Rn
A path is a continuous map r: [a,b] to U, [a,b] in R such that r(a) = p and r(b) = q
36
Define path connected for U, a subset of Rn
for all p,q in U, there is a path r:[a,b] to U such that r(a) = p and r(b) = q
37
38
Define sequential compactness for K, a subset of Rn
39
40
K, a subset of R2 is sequentially compact if and only if K is closed and bounded
41
State and prove the extreme value theorem a subset K in Rn
42
Let V = { (x,y) : xy not equal to 0}. Prove V isn't path connected
43
What is meant by L(Rn, Rk) and M(k x n, R)
44
Define || (aij) ||2
45
Define the operator norm
46
What is the relationship between || A || and || (aij) ||2?
47
Prove that ||BA|| \<= ||B|| ||A||
48
Define the General Linear group
49
50
Define differentiability for a point p, in U, a subset of Rn
51
52
State the chain rule
53
Define directional derivative
54
Define the partial derivative
55
56
Define the Jacobian matrix
57
What condition must hold in the Jacobian matrix for p to be differentiable
it must exist at all points
58
Define continuously differentiable
59
What is the Jacobian form of the chain rule?
60
Define grad f
61
Given f: Rn to R and g:R to R whats the jth partial derivative of g(f(x)), and then define grad g(f(x))
62
define d/dt f(r(t)) for f:Rn to R and r:R to Rn
63
64
Define a change of variables
65
66
State the Inverse function theorem
67
68
State the Implicit function theorem
69
Define a vector field
70
Define the Curve Cpq
71
Define the tangential line integral
72
73
74
Define a gradient field
If a vector field v is the gradient of a function f : U → R then v is called a gradient field.
75
State the fundamental theorem of calculus for a gradient vector field
76
0
77
Define conservative
78
79
Theorem: A vector field v: U to Rn is a gradient field if and only if its conservative
80
When is f called a scalar potential of v
When v = grad f
81
Define v perp, and then the normal to a curve C
82
Define the flux of a vector field in R2
83
Derive greens theorem for a rectangle
84
Define a region in Rn
85
Define curl
86
Define a positively oriented regular parameterisation
87
State Greens theorem for a planar region
88
Give the equation for the flux of of v across the boundary of omega
89
Define the divergence of a vector field
90
State the divergence theorem
91
Give the two equations for the flux of v across a surface S in R3
92
State the divergence theorem in R3
93
Define a radial function
94
Define Hess f(p)
95
When do second order partial derivatives commute?
D2f exists
the second partial derivatives are continuous
96
State Taylor's theorem, both for the 1 variable case, and otherwise
97
State the conditions for when a symmetric matrix is
i) positive definite
ii) positive semidefinite
iii) negative definite
iv) negative semidefinite
v) indefinite
98
State the second order derivative test
99
State the definitiveness test for 2x2 symmetric matrices
100
