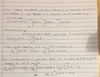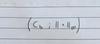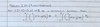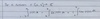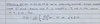Analysis III Flashcards
Define a Partition
Define Upper Riemann Sums and Lower Riemann Sums
Define the Upper and Lower Riemann Integrals
When is a function Riemann integrable, and what is the integral equal to
Only when U(f) = L(f), and then the integral is equal to this value
Define a refinement
Theorem: Let f:[a,b] to R be a bounded function and P,Q refinements of [a,b] where Q is a refinement of P, then L(f,P) <= L(f,Q) <= U(f,Q) <= U(f,P)
Theorem: Let f:[a,b] to R bea bounded function and P,Q two partitions of [a,b]. Then L(f,P) <= U(f,Q)
Theorem: Let f:[a,b] to R be a bounded function. Then f is integrable if and only if for every ε > 0 there exists a partition P of [a,b] such that U(f,P) - L(f,P) < ε
Define continuity of f
Define uniform continuity of f
Let f:[a,b] to R be a continuous function. Then it’s uniformly continuous
Let f:[a,b] to R be a continuous function. Then it’s Riemann integrable
Theorem: Let f:[a,b] to R be a monotonic function. Then it’s Riemann integrable
Let f,g:[a,b] to R be integrable. Then f + g is integrable
Theorem: Let f,g:[a,b] to R be integrable, and c in R. Then cf is integrable
Let f:[a,b] to R be integrable. Define m = inf f and M = sup f, whats the relationship between m(b-a), M(b-a) and the integral
m(b-a) <= integral <= M(b-a)
Let f:[a.b] to R and c in (a,b). Then f is integrable on [a,b] if and only if it’s integrable on [a,c] and [c,b]
Let f:[a,b] to R be bounded, integrable and Ф: R to R a continuous function. Then Ф o f is integrable
Theorem: Let f,g:[a,b] to R be integrable functions. Then fg is integrable, and if 1/g is bounded then f/g is integrable
Let f:[a,b] to R be integrable for every [c,b] with a < c. Define the improper integral of f on [a,b]
Let f:[a,b] to R be integrable for every [a,c] with c < b. Define the improper integral of f on [a,b]
Let f:[a,b] to R be a function integrable on any closed interval not containing c in [a,b], ie integrable on all [a,c - epsilon] and [c+ + delta, b]. Define the improper integral
Let f:[a, inf) to R be integrable for every interval [a,y] for a < y < inf. Define the improper integral
Let g:(inf, b) to R be integrable for every interval [y,b] for -inf < y < b. Define the improper integral
Let f:R to R be a function integrable on every bounded interval [a,b]. Define the improper integal
Define pointwise convergence of sequences
Define uniform convergence of sequences
Define uniformly cauchy for sequences
Theorem: A sequence (fn) is uniformly cauchy if and only if its uniformly convergent
Let (fn) be a sequence of continuous functions in Omega that converge uniformly to f: Omega to R. Then f is continuous
What does this represent?
The space of bounded, continuous functions with the uniform norm
Define continuity on f: R2 to R
Define uniform continuity on f: R2 to R
For a sequence (fk) of functions define partial sums and both pointwise and uniform convergence
Let I be an interval in R. When is a function f: I to R
i) increasing
ii) decreasing
i) f(x) <= f(y) when x < y
ii) f(x) >= f(y) when x < y
Given f:[a,b] to R define total variation and state the conditions for bounded variation
Define absolute continuity for f:[a,b] to R
Define uniform lipschitz for a sequence of functions
Theorem: Suppose that fn converges pointwise to f and fn is uniformly lipschitz. Then f is lipschitz
Theorem: Let f:[a,b] to R be an absolutely continuous function. Then f is of bounded variation
Define convergence for (zn) in C
Define open and closed for a set Omega in C
Define sequential compactness in C
What is the matrix representation of the complex number a + bi
a - b
b a
Define continuity in C
Define complex differentiability on a open set Omega in C
What are the Cauchy-Riemann equations?
ux = vy
uy = -vx
When is f analytic (or holomorphic) in C?
Define convergence of infinite sums, with entries in C
Define absolute convergence of infinite sums, with entries in C
State the Ratio test for infinite sums
State the root test for infinite sums
What is the derivative of the infinite sum (anzn)n=0n=inf with radius of convergence R
Let (anzn) from n=0 to infinity be a power series with radius of convergence R. What is f(n)(0)
ann!
Define the power series for the following functions
i) ez
ii) cos(z)
iii) cosh(z)
iv) sin(z)
v) sinh(z)
State the exponential identities for cos(z), sin(z), cosh(z) and sinh(z). Prove the result for cos(z)
For a function f:[a,b] to C define the complex integral
Define connected and simply connected on a subset omega of C
Theorem: Every non-constant polynomial p on C has a root. ie there exists an a in C such that p(a) = 0
If f:C to C is harmonic, what two equations are satisfied
uxx + uyy = 0
vxx + vyy = 0
Theorem: Let f: C to C be analytic. Then if |f| is also analytic, f must be a constant
