Algebra II - Groups Flashcards
Define a group
When is a group abelian
when it’s commutative ie when ab=ba for all a,b
If g,h are elements of a multiplicative group G, what is (gh)-1
h-1g-1
Define Kstar for a field K
Kstar = K \ {0}
What is GLn(K) and SLn(K)? Are they abelian?
GLn(K) is the set of invertible n x n matrices with entries in K. SLn(K) is the set of n x n matrices with determinant 1. They are both non-abelian
What is Sym(X)
the set of permutations of X; bijections from X to X
Define order of a group G
The number of elements in G, denoted | G |
Define the order of an element g in G
The smallest natural number n such that gn = 1. Denoted o(g) or | g |
Define an isomorphism between two groups
Proposition: Any two infinite cyclic groups are isomorphic. For a positive integer n, any two cyclic groups of order n are isomorphic
When is a subset H of a group G a subgroup
When it forms a group under the same operation as G
If H is a non-empty subset of a group G, when is it a subgroup (2 conditions)
h,g in H implies gh in H
h in H implies h-1 in H
Lemma: Let G be a group with H,K subgroups of G. Then HnK is also a subgroup of G
Define the direct product of two multiplicative groups G,H
G x H is the set { (g,h) | g in G, h in H}
What is the Klein Four Group
{1,a,b,c}
a,b,c have order 2, and the product of any two of these elements is the other one
What could a group of order 4 be isomorphic to?
Either a cyclic group or the Klein Four group
Define the Dihedral group of order 2n
It is the isometries of P, which are
i) n rotations (2(pi)k)/n around the centre of P, denoted ak
ii) n reflections about lines that pass through the centre of P, denoted b
Then G = { ak | 0 < k <= n} union {akb | 0 < k <= n}
In D2n what is ba?
a-1b and a-1 = an-1
When do elements {g1,…….,gr} generate a group G
if every element of G can be obtained by repeated multiplication of the gi and their inverses
Proposition: Let G be a group of order 2n generated by two elements a,b with an = 1, b2 = 1 and ba = a-1b. Then G is isomorphic to D2n
Proposition: Let G be a group of order mn generated by two elements a and b that satisfy the equations am = 1, bn = 1 and ab = ba. Then G is isomorphic to Cm x Cn
Define the Quaternion group, Q8
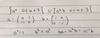
Define the right coset Hg for g in G
{hg | h in H}
For g,k in G, give the two equivalent conditions to k in Hg
Hg = Hk
kg-1 in H
State Lagrange’s theorem
Let G be a finite group and H a subgroup of G. Then the order of H divided the order of G. Furthermore |G| = |H| x [G:H]
Define the index of H in G
it’s the number of distinct cosets of H in G
Proposition: Let G be a finite group. Then for any g in G the order |g| of g divides the order |G| of G
Proposition: Let G be a group having prime order p. Then G is cyclic and G is isomorphic to Cp
When is a subgroup H of G normal?
If the left and right cosets gH and Hg are equal for all g in G
Proposition: If G is any group and H is a subgroup with [G : H] = 2, then H is a normal subgroup of G
Proposition: Let H be a subgroup of the group G. Then H is normal in G if and only if ghg-1 is in H for all g in G and h in H
Lemma: Let G be a group in which g2 = 1 for all g in G, and let a,b be distinct non-identity elements of G. Then {1, a, b, ab} is a subgroup of order 4
Proposition: Let G be a group of order 6. Then G is isomorphic to either C6 or D6
If N is a normal subgroup of G and Ng, Nh are cosets of N in G, what is (Ng)(Nh)
Ngh
Theorem: Let N be a normal subgroup of a group G. Then the set G/N of right cosets Ng of N in G forms a group under multiplication
Define a homomorphism between groups
Proposition: Let phi: G to H be a homomorphism. Then phi is injective if and only if ker(phi) = {1G}
Proposition: Let phi: G to H be a homomorphism. Then im(phi) is a subgroup of H
State the first isomorphism theorem for groups
State the second isomorphism theorem for groups
Let G be a group and X a set. Define an action of G on X
Define the kernel of an action of G on X, when is the action faithful?
State Cayley’s theorem
Every group G is isomorphic to a permutation group (a subgroup of Sym(X) for some set X)
For an action of G on X, define the orbit
What is the stabilisier of x in G?
StabG(x) = { g in G | g . x = x}
Prove that StabG(x) is a subgroup of G, where G acts on X
State and prove the Orbit-Stabiliser theorem
Define the conjugation action, and both the conjugate classes and centraliser
Given a permutation in cyclic notation, how do we obtain the conjugate fgf-1 of g
Replace each element x in X in the cycles of g by f(x)
Define cycle type of a permutation
It has cycle type 2r23r3…… if it has exactly ri cycles of length i
Proposition: A4 has no subgroup of order 6
Define a Sylow p-subgroup of G
State Sylow’s theorem
If G is a group of order pnm, define Sylp(G)
Sylp(G) = {H is a subgroup of G | |H| = pn}
Give two conditions on | Sylp(G) |
|Sylp(G)| divides [G:P]
|Sylp(G)| = 1 if and only if P is a normal subgroup of G
Proposition: A simple abelian group is cyclic of prime order
Lemma: There are no simple groups of order 24
