Mathematical Statistics - 1,2

Question 1

Define a statistical model

Answer 1

A statistical model is one that describes random variation of data in a way controlled by parameters

Question 2

Define a random variable

Answer 2

A random variable X on a probability space (Omega, f, P) is a function X: Omega to R

Question 3

For a discrete random variable X give the equation for

i) E[X]
ii) CDF F_X(x)
iii) E[g(X)] for a function g: R to R

Answer 3

Question 4

For a continuous random variable X give the equation for

i) PDF
ii) E[X]
iii) E[g(X)]

Answer 4

Question 5

Give the two equations for Variance of X

Answer 5

Question 6

What is the n^th moment of X

Answer 6

E[Xⁿ]

Question 7

Define the Moment generating function

Answer 7

Question 8

When are random variables X₁,…….,X_n independent

Answer 8

Question 9

Whats the relationship between M_X+Y(u), M_X(u) and M_Y(u)

Answer 9

Question 10

Give the probability of A given B

Answer 10

Question 11

Define the Bernoulli(p) random variable and give the equation for

i) E[X]
ii) Var[X]
iii) MGF

Answer 11

Question 12

Define a Binomial(n,p) random variable and give the equation for i) E[X]

ii) Var[X]
iii) MGF

Answer 12

Question 13

Define a Geometric(p) random variable and give the equation for i) E[X]

ii) Var[X]
iii) MGF

Answer 13

Question 14

Answer 14

Question 15

Define a Poisson(Lamda) random variable and give the equation for i) E[X]

ii) Var[X]
iii) MGF

Answer 15

Question 16

Define a Categorical random variable

Answer 16

Question 17

Define a uniform random variable and give the equation for

i) E[X]
ii) Var[X]
iii) CDF

Answer 17

Question 18

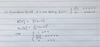
Define an exponential(lamda) random variable and give the equation for

i) E[X]
ii) Var [X]
iii) MGF

Answer 18

Question 19

What is the Gamma function?

Answer 19

Question 20

Define the Gamma(v,lamda) distribution and give the equations for

i) E[X]
ii) Var[X]
iii) MGF

Answer 20

Question 21

Answer 21

Question 22

Define a Normal(0,1) distribution and a Normal(mu, sigma²) distribution, and give the MGF for the latter case

Answer 22

Question 23

What is the chi-squared distribution

Answer 23

Question 24

Give the equation for the marginal distributions of an n dimensional random vector that is

i) discrete
ii) continuous

Answer 24

Question 25

Give the two equations for Covariance

Answer 25

Cov[X,Y] = E[(X - E[X])(Y - E[Y]) = E[XY] - E[X]E[Y]

Question 26

What is Var[aX]

Answer 26

a²Var[X]

Question 27

What is Var[aX + bY]

Answer 27

a²Var[X] + 2abCov[X,Y] + b²Var[Y]

Question 28

If X is absolutely continuous on Rⁿ and g: Rⁿ to R is continuously differentiable with a continously differentiable inverse h. Then if Y=g(X), what is f_y(y)

Answer 28

J_h(y)f_x(h(y)) where J_h is the Jacobian of h

Question 29

Answer 29

Question 30

State Fishers Theorem

Answer 30

Question 31

State and prove Markov's inequality

Answer 31

Question 32

State Chebyshev's inequality

Answer 32

Question 33

Define convergence in probability

Answer 33

Question 34

State the weak law of large numbers

Answer 34

Question 35

Define weak convergence

Answer 35

Question 36

State the Central Limit Theorem

Answer 36

Question 37

Define convergence in quadratic mean

Answer 37

Question 38

State and prove the Continuous Mapping Theorem

Answer 38

Question 39

State the Law of total variance

Answer 39

Var[Y] = E[Var[Y | X] ] + Var[E[ Y | X] ]