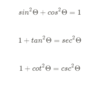Module 05:

Question 1

Find sin θ if cot θ = - 2 and cos θ < 0. (2 points)

Answer 1

√5/5

Question 2

Use basic identities to simplify the expression. (2 points)

cos θ - cos θ sin²θ

1. sec²θ
2. sin θ
3. tan²θ
4. cos³θ

Answer 2

3.cos³θ

Question 3

Use basic identities to simplify the expression. (2 points)

1/cot²θ+ sec θ cos θ

Answer 3

sec²θ

Question 4

Simplify the expression. (2 points)

(csc²x sec²x)

÷

(sec² x + csc²x)

1. sin²x
2. cos²x
3. -1
4. 1

Answer 4

4. 1

Question 5

Factor the algebraic expression below in terms of a single trigonometric function.

csc ²x - 1

Answer 5

Question 6

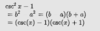
Find all solutions in the interval [0, 2π).

cos²x + 2 cos x + 1 = 0

Answer 6

x = π

Question 7

Find all solutions in the interval [0, 2π).

(sin x)(cos x) = 0

Answer 7

0, π/2; π, 3π/2

Question 8

Find all solutions to the equation.
cos²x + 2 cos x + 1 = 0

Answer 8

cos2x + 2cosx + 1 = 0

(cosx + 1)2 = 0

cosx + 1 = 0

cosx = -1

x = π + 2πn

Question 9

Find an exact value:

sin(11π/12)

Answer 9

(√6 - √2)/4

Question 10

Find an exact value:

cos (19π/12)

Answer 10

(√6 - √2)/4

Question 11

Write the expression as either the sine, cosine, or tangent of a single angle. (2 points)

sin 48° cos 15° - cos 48° sin 15°

1. cos 33°
2. cos 63°
3. sin 63°
4. sin 33°

Answer 11

4. sin 33°

Question 12

Write the expression as either the sine, cosine, or tangent of a single angle:

sin (π/2)cos(π/7) + cos(π/2)sin(π/7)

Answer 12

Question 13

Find an exact value. (2 points)

cos 15°

Answer 13

√6 +√2

÷

4

Question 14

Write the expression as either the sine, cosine, or tangent of a single angle. (2 points)

sin 48° cos 15° - cos 48° sin 15°

1. cos 33°
2. cos 63°
3. sin 63°
4. sin 33°

Answer 14

4. sin 33°

Question 15

Find all solutions to the equation in the interval [0, 2π). (3 points)

cos 4x - cos 2x = 0

Answer 15

0, π/3, 2π/3, π, 4π/3, 5π/3

Question 16

Rewrite with only sin x and cos x. (3 points)

sin 3x

Answer 16

2 cos²x sin x + sin x - 2 sin³x

Question 17

Find the exact value by using a half-angle identity: sin(7π/8)

Answer 17

Question 18

.

Find cot θ if csc θ = √17/4 and tan θ > 0.

Answer 18

1/4

Question 19

Simplify the expression: cot x sin x - sin (π/2 - x) + cos x (1 point)

1. cos x
2. sin x
3. 2 sin x
4. 2 cos x

Answer 19

1. cos x

Question 20

Find tan θ if sec θ = √37/6 and sin θ < 0

Answer 20

-1/6

Question 21

Find all solutions in the interval [0, 2π). (1 point)

sec²x - 2 = tan²x

Answer 21

No solution

Question 22

Find all solutions to the equation. (1 point)

sin x = √3/2

Answer 22

Question 23

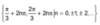
Find an exact value: sin (-11π/12)

Answer 23

(√2 - √6)

÷

4

Question 24

Write the expression as the sine, cosine, or tangent of an angle. (1 point)

sin 9x cos x - cos 9x sin x

1. sin 10x
2. cos 8x
3. sin 8x
4. cos 10x

Answer 24

3. sin 8x

Question 25

Write the expression as the sine, cosine, or tangent of an angle. (1 point) cos 112° cos 45° + sin 112° sin 45° 1. sin 157° 2. sin 67° 3. cos 157° 4. cos 67°

Answer 25

**4.** cos 67°

Question 26

Rewrite with only sin x and cos x. (1 point) sin 2x - cos 2x

Answer 26

2 sinx cosx - 1 + 2 sin²x

Question 27

Find the exact value by using a half-angle identity. (1 point) sin 22.5°

Answer 27

1/2 √(2 - √2)

Question 28

Find all solutions to the equation in the interval [0, 2π). (1 point) cos x = sin 2x

Answer 28

π/6, π/2, 5π/6, 3π/2

Question 29

Rewrite with only sin x and cos x. (1 point) **sin 2x - cos x** 1. 2 sin x cos²x 2. sin x 3. cos x (2 sin x - 1) 4. 2 sin x

Answer 29

**3.** cos x (2 sin x - 1)

Question 30

Verify the identity

Answer 30

Question 31

Find cos θ if sin θ = -12/13 and tan θ \> 0

Answer 31

-5/13

Question 32

Use basic identities to simplify the expression. (6 points) **sin²θ + tan²θ + cos²θ** 1. sec²θ 2. cos³θ 3. sin θ 4. tan²θ

Answer 32

**1.** sec²θ

Question 33

Write the expression as the sine, cosine, or tangent of an angle. (6 points) sin 5x cos x - cos 5x sin x 1. cos 6x 2. cos 4x 3. sin 6x 4. sin 4x

Answer 33

**4.** sin 4x

Question 34

Rewrite with only sin x and cos x. (6 points) sin 2x - cos 2x 1. 2 sin²x - 2 sin x cos x + 1 2. 2 sin x 3. 2 sin²x + 2 sin x cos x - 1 4. 2 sin²x - 2 sin x cos x - 1

Answer 34

**3.** 2 sin²x + 2 sin x cos x - 1

Question 35

Verify the identity. (7 points) cos 4u = cos²2u - sin²2u

Answer 35

Question 36

Verify the identity.

Answer 36

Question 37

What are the repicrocal identities?

Answer 37

Question 38

What are the quotient identities?

Answer 38

Question 39

What are the Pythagorean identities?

Answer 39

Question 40

What is the confunction identities?

Answer 40

Question 41

What is the Even/Odd Identities?

Answer 41

Question 42

What are the methods for solving trigonometric equations?

Answer 42

**Step 01: Solve the equations for the trigonometric value** **Step 02: Find all solutions, or general solutions, by adding:** 1. 2π n to the radians measures for sine and cosine 2. πn to radian measures for tangent and cotangent **Step 03: Final all solutions with specific interval by substituting random integers for n.** 1. Accept: solutions within interval 2. Reject: solutions outside interval Remember, x-coordinates represent cosine values and y-coordinates represent sine values.

Question 43

What are the sun and different formulas?

Answer 43

Question 44

What are the Multi-Angle Formulas?

Answer 44

Question 45

What are the Half-Angle Formulas?

Answer 45

Question 46

What are the Power Reducing Formula?

Answer 46