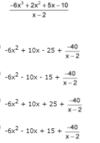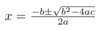Module 02: Polynomial and Rational Functions Flashcards
Find the vertex of the graph of the function.
f(x) = (x + 4)2 + 4 (2 points)
- (0, -4)
- (4, 0)
- (4, -4)
- (-4, 4)
4. (-4, 4)
Find the vertex of the graph of the function.
f(x) = 2x2 + 8x + 10 (2 points)
- (3, -1)
- (2, -2)
- (-2, 2)
- (-1, 3)
3. (-2, 2)
Write the quadratic function in vertex form.
y = x2 + 8x + 18
y = (x + 4)2 + 2
A projectile is thrown upward so that its distance above the ground after t seconds is given by the function h(t) = -16t2 + 704t. After how many seconds does the projectile take to reach its maximum height? Show your work for full credit. (2 points)
The projectile will take 22 seconds (t) to reach its maximum height at 7744.
Find the zeros of the function.
f(x) = 9x2 - 27x + 20
- 5 and 4
- -5 and -4
- -5/3 and -4/3
- 5/3 and 4/3
4. 5/3 and 4/3
Find the zeros of the function.
f(x) = 9x3 - 45x2 + 36x (2 points)
- 0, 1, and 4
- -1 and -4
- 1 and 4
- 0, -1, and -4
- 0, 1, and 4
Find the zeros of the polynomial function and state the multiplicity of each.
f(x) = 4(x + 7)2(x - 7)3
- 4, multiplicity 1; -7, multiplicity 3; 7, multiplicity 3
- -7, multiplicity 3; 7, multiplicity 2
- 4, multiplicity 1; 7, multiplicity 1; -7, multiplicity 1
- -7, multiplicity 2; 7, multiplicity 3
4. -7, multiplicity 2; 7, multiplicity 3
Find a cubic function with the given zeros. (2 points)
√2 , -√2 , -2
- f(x) = x3 + 2x2 - 2x + 4
- f(x) = x3 +2x2+ 2x - 4
- f(x) = x3 - 2x2 - 2x - 4
- f(x) = x3 + 2x2 - 2x - 4
4. f(x) = x3 + 2x2 - 2x - 4
Expand the following using either the Binomial Theorem or Pascal’s Triangle. You must show your work for credit.
(x - 5)5
See attachment
Divide using synthetic division, and write a summary statement in fraction form. (2 points)
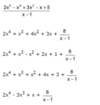
Answer: 3
Divide f(x) by d(x), and write a summary statement in the form indicated.
f(x) = x4 + 4x3 + 6x2 + 4x + 5; d(x) = x2 + 1
- f(x) = (x2 + 1)( x2 + 4x + 5) + 12x - 15
- f(x) = (x2 + 1)( x2 + 4x + 5)
- f(x) = (x2 + 1)( x2 - 4x + 5)
- f(x) = (x2 + 1)( x2 - 4x + 5) + 12x - 15
2. f(x) = (x2 + 1)( x2 + 4x + 5)
Find the remainder when f(x) is divided by (x - k).
f(x) = 3x3 - 4x2 - 3x + 14; k= 3
- 50
- 68
- -12
- 112
50
Use synthetic division to determine whether the number k is an upper or lower bound (as specified) for the real zeros of the function f.
k = -1; f(x) = 4x3 - 2x2 + 2x + 4; Lower bound?
YES or NO
YES
Use the Rational Zeros Theorem to write a list of all possible rational zeros of the function.
f(x) = 2x3 + 8x2 + 7x - 8
According to the Rational Zeros Theorem, p is the factors of the constant term of a0, which is 8. Therefore, p = 1, 2, 4, 8. Next, q is the leading coefficient of an, which is 2, so the factors of q are 1 and 2. According to the Rational Zeros Theorem, the possible zeros is p/q.
Write the sum or difference in the standard form a + bi. (2 points)
( 7 + 5i) - ( -9 + i)
- 16 + 4i
- -16 - 4i
- 16 - 4i
- -2 + 6i
- 16 + 4i
Write the product in standard form. (2 points)
( 4 + 7i)( 7 + 7i)
-21 + 77i
Find the product of the complex number and its conjugate
1 + 3i
- 1 + 9i
- 10
- -8
- 1 - 9i
2. 10
Write the expression in standard form:
3/ (3-12i)
1/17 + 4/17i
Find the real numbers x and y that make the equation true
-4 + yi = x + 3i
According to the Rule of Equality of Complex Numbers, a+bi=c+di, only if a=c and b=d. Therefore, in order for the above equation to be equal, x=-4 and y=3.
Write a polynomial function of minimum degree with real coefficients whose zeros include those listed. Write the polynomial in standard form. (2 points)
4, -8, and 2 + 5i
f(x) = x4 - 19x2 + 244x - 928
State how many imaginary and real zeros the function has. (3 points)
f(x) = x3 + 5x2 + x + 5
- 0 imaginary; 3 real
- 1 imaginary; 2 real
- 3 imaginary; 0 real
- 2 imaginary; 1 real
4. 2 imaginary; 1 real
Write a linear factorization of the function.
f(x) = x4 + 64x2
f(x) = x2(x + 8i)(x - 8i)
State the domain of the rational function. (2 points)
f(x) = 13/ (10-x)
- All real numbers except -10 and 10
- All real numbers except 13
- All real numbers except 10
- All real numbers except -13 and 13
3. All real numbers except 10
State the vertical asymptote of the rational function. (2 points)
f(x) = [(x-6)(x+6)] / (x2-9)
x = 3, x = -3
State the horizontal asymptote of the rational function. (2 points)
f(x) = (5x+1) / (9x-2)
- None
- y = 3/2
- y = 5/9
- y = 0
3. y = 5/9
State the horizontal asymptote of the rational function. (2 points)
f(x) = (x+9) / (x2+2x+3)
y = 0
Find the vertex of the graph of the function. (5 points)
f(x) = (x + 6)2 + 3
- (0, -6)
- ( 3, 0)
- ( 3, -6)
- ( -6, 3)
4. ( -6, 3)
Find the vertex of the graph of the function. (5 points)
f(x) = 2x2 - 8x + 6
(2, -2)
Find the axis of symmetry of the graph of the function. (5 points)
f(x) = 2x2 - 4x
- x = 1
- x = 3
- x = 0
- x = -2
- x = 1
Write the quadratic function in vertex form. (5 points)
y = x2 - 2x + 5
- y = (x + 1)2 - 4
- y = (x - 1)2 - 4
- y = (x + 1)2 + 4
- y = (x - 1)2 + 4
4. y = (x - 1)2 + 4
A projectile is thrown upward so that its distance above the ground after t seconds is h = -16t2 + 440t.
After how many seconds does it reach its maximum height? (5 points)
14 seconds
.
Find the zeros of the function. (5 points)
f(x) = x2 - 6x + 8
4 and 2
Find the zeros of the function.
f(x) = 4x3 - 12x2 - 40x
0, 5, -2
Find the zeros of the polynomial function and state the multiplicity of each. (5 points)
f(x) = 5(x + 6)2(x - 6)3
-6, multiplicity 2; 6, multiplicity 3
Find a cubic function with the given zeros. (5 points)
-2, 5, -6
f(x) = x3 + 3x2 - 28x - 60
Divide using synthetic division, and write a summary statement in fraction form.
Answer: 2
Use the Rational Zeros Theorem to write a list of all potential rational zeros.
f(x) = 14x3 + 56x2 + 2x - 7
±1, ± 1/2, ±7, ± 7/2, ± 1/7, ± 1/14
Write the expression in standard form:
5/ (2-14i)
1/20 + 7/20 i
Write a polynomial function of minimum degree with real coefficients whose zeros include those listed. Write the polynomial in standard form. (5 points)
4, -8, and 2 + 3i
f(x) = x4 - 35x2 + 180x - 416
State how many imaginary and real zeros the function has. (5 points)
f(x) = x4 - 15x2 - 16
- 4 imaginary; 0 real
- 3 imaginary; 1 real
- 2 imaginary; 2 real
- 0 imaginary; 4 real
3. 2 imaginary; 2 real
Write a linear factorization of the function. (5 points)
f(x) = x4 + 81x2
f(x) = x2 (x + 9i)(x - 9i)
Using the given zero, find one other zero of f(x). (5 points)
3 - 6i is a zero of f(x).= x4 - 6x3 + 46x2 - 6x + 45.
- 3 - i
- 1
- 3 + 6i
- 3 + i
3. 3 + 6i
State the domain of the rational function. (5 points)
f(x) = 17/(5-x)
All real numbers except 5.
What is the quadratic function?
f(x) = ax2 + bx + c
a, b, c → real numbers (not zero)
- u-shaped > parabola
- symmetric
Vertex: interception with axis
Opens upwards: leading coefficient is positive
Opens downwards: leading coefficient negative
- if a > 0, then the parabola opens upward, and if a < 0, the parabola opens downward.*
- *
Simplest: f(x) = ax2
Find the vertex: -b/2a
a2 + bx + c
How do you find the vertex from the quadratic function?
Find the vertex: -b/2a
What is the vertex form?
f(x) = a(x - h)2 + k
- Vertex point: (h, k)
- axis x = h
What is the quadratic formula?
What is the Binomial Theorem?
What is Pascal’s Triangle?
What is the Leading Coefficient Test?
Rise and falling of the graph dependent:
-
degree is odd or even
- if the degree is even, the graph will rise at both ends,
- if the degree is odd, then the graph will rise at one end and fall at the other end
-
leading coefficient test
- coefficient positive: falls to the left and rises to the right
- coefficient negative: rises to the left and falls to the right
What is the Zeros of Polynomial Functions test?
Zeros → interception with x-axis
- x = a is a zero of the function
- x = a is a solution for the polynomial set equal to 0
- (x - a) is a factor of the polynomial
- (a, 0) is an x-intercept of the function
What is the Intermediate Value Theorem?
Let a and b real numbers such that a < b. If f(a) ≠ f(b), then interval (a, b), f takes on every value between f(a) and f(b)
- if (a, f(a)) and (b, f(b)) are 2 points → every x value between a and b takes on every y-value between f(a) and f(b)
What is the Extreme Value Theorem?
if function f(x) continuous on a closed interval [a, b] then f(x) has both a maximum and a minimum on [a, b]
theorem is stating that if you graph a curve from x = a and never pick your pencil up until x = b, then that curve is guaranteed to have a maximum and minimum:
- x values at the endpoint of the curve [$x = a$ & $x = b$]
- any x value where the curve hits a peak or a valley
What is the Remainder Theorem?
If a polynomial f(x) ÷ (x - k), the remainder is r = f(k).
This means we can find a point on the graph of a function by choosing a value k for x = k and using division to get a remainder. The remainder will be the y coordinate of the point on the graph.
What is the Factor Theorem?
A polynomial f(x) has a factor ( - k) if, and only if, f(k) = 0.
If remainder is a 0 = being a factor
What is the Rational Zero Test?
If: it has a integer coefficient
f(x) = anxn = an-1xn-1 + … + a1x + a0
Every rational zero of f(x) has a form:
Rational Zero
- p/q (p and q have no common factors other than 1)
- p factor of the constant term a0
- q factor of the leading coefficient of an
Note that the Rational Zero Test does not guarantee that any of these values will be zeros; it just states that if the zeros are rational, then they will come from this list.
What is the Descartes’ Rule of Signs?
- Number of positive zeros:
- equal to the number of sign changes between consecutive coefficients in f(x)
- less than said number by a multiple of 2
- Number of negative zeros:
- equal to the number of sign changes between f(-x)
- less than said number by a multiple of 2
What is the steps to find the zeros?
Step 01: Use the Rational Zero test to determine the list of possible zeros
Step 02: Use the Descartes’ Rule of Signs to narrow it down
Step 03: Use sythetic division to see which of the remainders is an actual zero
What is the Bounds for Real Zeros?
f(x) is divided by (x-c) then:
-
c > 0 → each number in the last row is positive or zero
- c upper bounds for real zeros of f
- upper bound = positive
-
c < 0 → number in the last row are alternately positive and negative
- c lower bounds for real zeros of f
- lower bounds = negative
What is the Rule of the Equality of Complex Numbers?
What is the Rule of the Addition and Subtraction of Complex Numbers?
if a + bi and c + di are two complex numbers:
Sum: (a + bi) + (c + di) = (a + c) + (b + d)i
Difference: (a + bi) - (c + di) = (a - c) + (b - d)i
Some of the properties for real numbers are also valid for complex numbers. They include the associative property of addition and multiplication, the commutative property of addition and multiplication, and the distributive property of multiplication over addition.
How do you plot complex numbers?
x-axis → real axis
y-axis → imaginary axis
a + bi
- a = real axis
- b = imaginary axis
What are complex conjugates?
Each of two complex numbers having their real parts identical and their imaginary parts of equal magnitude but opposite sign.
z = a + bi
z = a - bi
How does division with complex numbers work?
Step 01: Determine complex conjugate of the denominator
Step 02: Multiple the numerator and the denominator with the complex conjugate
What is the Fundamental Theorem of Algebra?
If f(x) is a polynomial of degree n, where n > 0, f has at least one zero in the complex number system.
expand our set of zeros to the complex numbers, we can say that every nth degree polynomial has exactly n zeros.
set of complex numbers → one imaginary number and one real number
What is the Linear Factorization Theorem?
If f(x) has a polynomial degree of n:
f(x) = anxn + an-1xn-1 + … + a1x + a0
n > 0, f has precisely n linear factors
f(x) = an(x-c1)(x-c2)(x-c3) … (x-cn)
- c1, c2, c3 → complex numbers
- an → leading coefficient
What are Rational Functions?
What is the vertical and horizontal asymptotes?
Horizontal Asymptotes
The line x = a is a vertical asymptotes of the graph f is f(x) approaches b as x approaches infinity or x approaches negative infinity
Vertical Asymptotes
The line y = b is a horizontal asymptote of the graph f is f(x) approaches b as x approaches infinity or x approaches negative infinity
What are the asymptotes of rational functions?
What are the 5 characteristics of graphs of rational functions?
- the y-intercept (if any) is the value of f(0)
- the x-intercept (if any) are the zeros of the numerator, the solution is p(x) = 0
- vertical asymptotes (if any) are the zeros of the denominator, the solution is p(x) = 0
- horizontal asymptotes (if any) is the value that f(x) approaches as x increases or decreases
- determine the behavior of the graph between and to the left and right of each x-intercept
What are slant asymptotes?
numerator has exactly one more degree than the denominator → slant asymptote
- Example
- For the function f(x) = (x2 - 4x + 3) / (x + 2), find the slant asymptote.*
- Dividing the denominator into the numerator gives (x - 6) + 15 / (x + 2), and the slant asymptote would be y = x - 6.*
What is the difference between the vertical asymptotes and holes?
Vertical asymptotes: the zeros of q(x)
R(x) = p(x)/q(x)
Holes in the Asymptotes: Zeros of the denominator gets cancelled out when R(x) is put in a lowest term
