Brainscape's Knowledge GenomeTM

Browse over 1 million classes created by top students, professors, publishers, and experts.


See full index

Honors Pre-Calculus > Module 04: Trigonometric Functions > Flashcards

Module 04: Trigonometric Functions Flashcards

1
Q

Convert the angle 13°38’35” to decimal degrees, and round to the nearest hundredth of a degree. (2 points)

  1. 13.70°
  2. 13.65°
  3. 13.60°
  4. 13.64°
A

4. 13.64°

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
2
Q

Convert 17.47° to degrees, minutes, and seconds. (2 points)

  1. 17°28’18”
  2. 17°28’0”
  3. 17°28’12”
  4. 17°28’47”
A

3. 17°28’12”

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
3
Q

Convert 36° from degrees to radians.

A

π/5

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
4
Q

Convert the radian measure to degree measure. Use the value of π found on a calculator, and round answers to two decimal places. (2 points)

9π/12

  1. 135°
  2. 160°
  3. 270°
  4. 240π
A

1. 135°

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
5
Q

Use the arc length formula and the given information to find s. Show your work for full credit. (2 points)

r = 20 ft θ¸ = 19° s = ?

A

Θ = 19°

Θ = 19° * π/180

Θ = 19π/180

s=rΘ

s=(20ft)(19π180)

s=380π180

s=19π9

s=2.11π

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
6
Q

Find the exact values of sin A and cos A. Write fractions in lowest terms. (2 points)

  1. sin A = 4/3; cos A = 3/4
  2. sin A = 5/4 ; cos A = 5/3
  3. sin A = 3/5 ; cos A = 4/5
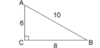
  4. sin A = 4/5 ; cos A = 3/5
A

4. sin A = 4/5 ; cos A = 3/5

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
7
Q

An acute angle θ is in a right triangle with sin θ = 2/3. What is the value of cot θ? (3 points)

A

√5/2

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
8
Q

An acute angle θ is in a right triangle with cos θ = 9/10. What is the value of sec θ? (2 points)

A

10/9

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
9
Q

Solve for x. Round your answer to two decimal places. Show your work for full credit. (3 points)

A

sinΘ=opp/hyp

sin(30­°)=10x

x=10sin(30°)

x=100.5

x=20

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
10
Q

Is the function cot t positive or negative in Quadrant II? (3 points)

Positive

Negative

A

Negative

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
11
Q

Find the measures of two angles, one positive and one negative, that are coterminal with π/5 . (2 points)

A

11π/5; -9π/5

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
12
Q

Evaluate sin 60° without using a calculator by using ratios in a reference triangle. (3 points)

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
13
Q

Determine the sign of sin 5π/4 without using a calculator. (2 points)

  1. Negative
  2. Positive
A

Negative

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
14
Q

Find the value of cos θ for the angle shown. (2 points)

  1. cos θ = 7/4
  2. cos θ = √33/4
  3. cos θ = 4/7
  4. cos θ = √33/7
A

cos θ = 4/7

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
15
Q
A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
16
Q

The point P(21, 28) is on the terminal side of θ. Evaluate sin θ. (3 points)

  1. 3/4
  2. 4/5
  3. 3/5
  4. 4/3
A

2. 4/5

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
17
Q

Choose the point on the terminal side of -45°. (2 points)

  1. (-3, -3)
  2. (4, -4)
  3. (5, 5)
  4. (-2, 2)
A

2. (4, -4)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
18
Q

Find the point on the terminal side of θ = -3π/4 that has an x coordinate of -1. Show your work for full credit. (3 points)

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
19
Q

Find the amplitude of y = -2 sin x. (2 points)

A

2

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
20
Q

Describe the transformations required to obtain the graph of the function f(x) from the graph of the function g(x).
f(x) = 4 cos x ; g(x) = cos x

  1. Vertical stretch by a factor of 4
  2. Horizontal stretch by a factor of 4
  3. Vertical shrink by a factor of 1/4
  4. Horizontal shrink by a factor of 1/4
A

1. Vertical stretch by a factor of 4

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
21
Q

Identify the maximum and minimum values of the function y = 8 cos x in the interval [-2π , 2π]. Use your understanding of transformations, not your graphing calculator. (3 points)

A
22
Q

Analyze the function f(x) = sec 2x.

Include:

  • Domain and range
  • Period and Amplitude
  • Two Vertical Asymptotes (6 points)
A
23
Q

From a boat on the lake, the angle of elevation to the top of a cliff is 26°1’. If the base of the cliff is 205 feet from the boat, how high is the cliff (to the nearest foot)? (2 points)

  1. 113 ft
  2. 110 ft
  3. 103 ft
  4. 100 ft
A

4. 100 ft

24
Q

From a balloon 760 feet high, the angle of depression to the ranger headquarters is 89°18’. How far is the headquarters from a point on the ground directly below the balloon (to the nearest foot)? (3 points)

A

9 ft

25
Q

Bob is driving along a straight and level road toward a mountain. At some point on his trip, he measures the angle of elevation to the top of the mountain and finds it to be 23°29’. Find the height of the mountain to the nearest foot if Bob is 16,194.6 feet from the center of the mountain at the base. (2 points)

  1. 7036 ft
  2. 7136 ft
  3. 70,357 ft
  4. 703,574 ft
A

1. 7036 ft

26
Q

A person is watching a boat from the top of a lighthouse. The boat is approaching the lighthouse directly. When first noticed, the angle of depression to the boat is 16°18’. When the boat stops, the angle of depression is 48°51’. The lighthouse is 200 feet tall. How far did the boat travel from when it was first noticed until it stopped? Round your answer to the hundredths place. (3 points)

A
27
Q

Convert the angle 35°58’38” to decimal degrees, and round to the nearest hundredth of a degree. (1 point)

A

35.98°

28
Q

Convert 210° from degrees to radians. Use the value of π found on a calculator, and round answers to four decimal places, as needed. (1 point)

A

7π/6

29
Q

Use the arc length formula and the given information to find r.

s = 16 cm, θ= 48°; r = ? (1 point)

A

r = 60/π cm

30
Q

An acute angle θ is in a right triangle with sin θ= 6/7 . What is the value of cot θ? (1 point)

A

√13/6

31
Q

Solve for x. Round your answer to 2 decimal places. (1 point)

  1. 3.71
  2. 13.21
  3. 5.94
  4. 8.25
A

2. 13.21

32
Q

Find the measures of two angles, one positive and one negative, that are coterminal with π/2 .

A

5π/2; -3π/2

33
Q

Find the amplitude y = 5 sin 1/2x. (1 point)

A

5

34
Q

Describe the transformations required to obtain the graph of the function f(x) from the graph of the function g(x).
f(x) = cos ; g(x) = cos x

  1. Horizontal stretch by a factor of 2
  2. Vertical stretch by a factor of 2
  3. Vertical shrink by a factor of 1/2
  4. Horizontal shrink by a factor of 1/2
A

2. Vertical stretch by a factor of 2

35
Q

Find the exact value of cos-1 (√3/2)

A

π/6

36
Q

Use a calculator to find the approximate value of cos-1(0.45). (1 point)

  1. 53.49°
  2. 63.26°
  3. 26.74°
  4. 24.23°
A

2. 63.26°

37
Q

Find the exact real value of arcsin (√3/2)

A

π/3

38
Q

Find the exact value of cos (arcsin (5/13)).

A

12/13

39
Q

From a boat on the lake, the angle of elevation to the top of a cliff is 14°28’. If the base of the cliff is 743 feet from the boat, how high is the cliff (to the nearest foot)? (1 point)

  1. 195 ft
  2. 192 ft
  3. 205 ft
  4. 202 ft
A

2. 192 ft

40
Q

What are the trigonometric functions forms?

A

Sine: y = a * sin (bx + c) + d

Cosine: y = a * cos (bx + c) + d

Tangent: y = a * tan (bx + c) + d

a is the amplitude (only for sin and cos)

Sine, Cosine, Secant and Cosecant all have a period of 2pi/b

Tangent and Cotangent have periods of pi/b

b helps us find the period from the equation period=2pi/b

Only tangent, cotangent, secant, and cosecant have asymptotes, and again, it depends which function we are working with as to what we need to do.

c is the phase shift (This is a horizontal shift of the curve)

d is the vertical shift

41
Q
A
42
Q
A
43
Q

What is the amplitude (a)?

A
  • a* → amplitude of the curve
  • determines verticle stretching or shrinking
  • range: -a ≤ y ≤ a

l a l → amplitude

44
Q

What is the period (b)?

A
  • b →* period of graph
  • determines horizontal stretching or shrinking

2π/b

Positive b

  • value < 1 stretches period beyond 2π
  • value > 1 shrinks period less than 2π

Negative b

  • sin(-x) = -sin(x)
  • cos(-x) = cos(x).
45
Q

What is the Phase Shift (c)?

A
  • c →* phase shift (horizontal) along x-axis
  • distance: c /d (phase shift)
46
Q

What is the endpoint on a graph?

A
  1. bx - c = 0
  2. bx - c = 2π
47
Q

What is the inverse sine function?

A
48
Q

What is the inverse cosine?

A
49
Q

What is inverse tangent?

A
50
Q

What is the angle of elevation and depression?

A

tangent-value = height-of-building ÷ distance-from-building

Angle of Elevation: Angle through which the eye moves up from horizontal to look at something above

Angle of Depression: Angle through which the eye moves up from horizontal to look at something above

51
Q
A

Honors Pre-Calculus (5 decks)

Brainscape helps you reach your goals faster, through stronger study habits.
© 2024 Bold Learning Solutions. Terms and Conditions