Brainscape's Knowledge GenomeTM


Top Flashcards (Certified)
All Flashcards

Honors Pre-Calculus > Module 03: Exponential and Logarithmic Functions > Flashcards

Module 03: Exponential and Logarithmic Functions Flashcards

1
Q

Decide if the function is an exponential function. If it is, state the initial value and the base. (2 points)

y = - 7.3 ⋅ 2x

  1. Exponential Function; base = - 14.6; initial value = 1
  2. Exponential Function; base = x; initial value = - 7.3
  3. Not an exponential function
  4. Exponential Function; base = 2; initial value = - 7.3
A

4. Exponential Function; base = 2; initial value = - 7.3

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
2
Q

Compute the exact value of the function for the given x-value without using a calculator. (2 points)

f(x) = 3x for x = -1

A

1/3

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
3
Q

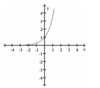
Choose the graph which matches the function. (2 points)

f(x) = 3x-4

A

Answer 03

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
4
Q

The graph of an exponential function is given. Which of the following is the correct equation of the function? (2 points)

  1. y = 0.65x
  2. y = 2.4x
  3. y = 3.5x
  4. y = 0.32x
A

4. y = 0.32x

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
5
Q

Decide whether the function is an exponential growth or exponential decay function, and find the constant percentage rate of growth or decay. (2 points)

f(x) = 3.6 ⋅ 1.04x

  1. Exponential growth function; 0.04%
  2. Exponential growth function; 104%
  3. Exponential decay function; 104%
  4. Exponential growth function; 4%
A

4. Exponential growth function; 4%

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
6
Q

Decide whether the function is an exponential growth or exponential decay function, and find the constant percentage rate of growth or decay. (2 points)

f(x) = 2229 ⋅ 0.9909x

  1. Exponential decay function; -0.91%
  2. Exponential growth function; -0.91%
  3. Exponential growth function; 0.0091%
  4. Exponential decay function; 0.0091%
A
  1. Exponential decay function; -0.91%
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
7
Q

Find the exponential function that satisfies the given conditions:

Initial value = 33, increasing at a rate of 7% per year (2 points)

  1. f(t) = 7 ⋅ 1.07t
  2. f(t) = 33 ⋅ 1.07t
  3. f(t) = 33 ⋅ 7t
  4. f(t) = 33 ⋅ 0.07t
A

2. f(t) = 33 ⋅ 1.07t

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
8
Q

Find the exponential function that satisfies the given conditions:

Initial value = 62, decreasing at a rate of 0.47% per week.

A

f(t) = 62 ⋅ 0.9953t

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
9
Q

The decay of 742 mg of an isotope is described by the function A(t)= 742e-0.03t, where t is time in years. Find the amount left after 84 years. Round your answer to the nearest mg. Show all of your work for full credit. (2 points)

A

A(84)=742e-0.03⋅84

A(84)=742e-2.52

A(84)=742(0.08045961)

A(84)=59.7

A(84)≈60mg

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
10
Q

Evaluate the logarithm. (2 points)

ln e4

  1. e4
  2. 1
  3. 4 ln e
  4. 4
A

4. 4

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
11
Q

Simplify: 10log109

A

9

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
12
Q

Find the following using a calculator. Round to four decimal places. (2 points)

log 0.47

  1. -0.8279
  2. -0.255
  3. -0.755
  4. -0.3279
A

4. -0.3279

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
13
Q

Assuming all variables are positive, use properties of logarithms to write the expression as a sum or difference of logarithms or multiples of logarithms. (2 points)

A

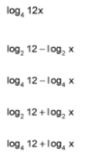
Answer: 04

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
14
Q

Assuming all variables are positive, use properties of logarithms to write the expression as a sum or difference of logarithms or multiples of logarithms. (2 points)

A

Answer: 02

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
15
Q

Use the product, quotient, and power rules of logarithms to rewrite the expression as a single logarithm. Assume that all variables represent positive real numbers. (2 points)

A

Answer: 01

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
16
Q

Use the change of base rule to find the logarithm to four decimal places. (2 points)
log9 0.877

A

-0.0597

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
17
Q

Solve: 4 logx + 3 logy

A

= log10 x4 + log10 y3 (Equality Property)

=logx4y3 (Product Property)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
18
Q

Find the exact solution to the equation. log5x = 2

  1. x = 52
  2. x = 5 ⋅ 2
  3. x = 25
A

1. x = 52

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
19
Q

Find the exact solution to the equation. (2 points)

6 - log9(x+10) = 5

  1. x = -2
  2. x = -1
  3. x = 1
  4. x = 19
A

2. x = -1

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
20
Q

Find the exact solution to the equation. (2 points)

5(6 - 2x) = 25

  1. x = 2
  2. x = 3
  3. x = 5
  4. x = -2
A
  1. x = 2
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
21
Q

Find the exact solution to the equation. (2 points)

125 (1/5) 1/4 = 5

  1. x = 9
  2. x = 2
  3. x = 1/2
  4. x = 8
A

4. x = 8

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
22
Q

Solve: 2ln (x + 2.8) = 3.2

23
Q

Decide if the function is an exponential function. If it is, state the initial value and the base. (1 point)

y = - 1.8 ⋅ 6x

  1. Not an exponential function
  2. Exponential Function; base = 6; initial value = - 1.8
  3. Exponential Function; base = - 10.8; initial value = 1
  4. Exponential Function; base = x; initial value = - 1.8
A

2. Exponential Function; base = 6; initial value = - 1.8

24
Q

Compute the exact value of the function for the given x-value without using a calculator. (1 point)

f(x) = (1/3)x for x = -1

    • 1/3
  2. 1/3
  3. 3
  4. -3
25
Q

The graph of an exponential function is given. Which of the following is the correct equation of the function? (1 point)

  1. y = 3.6x
  2. y = 1.9x
  3. y = 0.26x
  4. y = 0.74x
26
Q

Decide whether the function is an exponential growth or exponential decay function, and find the constant percentage rate of growth or decay. (1 point)

f(x) = 6 ⋅ 1.07x

  1. Exponential growth function; 107%
  2. Exponential decay function; 107%
  3. Exponential growth function; 7%
  4. Exponential growth function; 0.07%
A

3. Exponential growth function; 7%

27
Q

Decide whether the function is an exponential growth or exponential decay function, and find the constant percentage rate of growth or decay. (1 point)

f(x) = 2479 ⋅ 0.9948x

  1. Exponential decay function; 0.0052%
  2. Exponential growth function; -0.52%
  3. Exponential growth function; 0.0052%
  4. Exponential decay function; -0.52%
A

4. Exponential decay function; -0.52%​

28
Q

Find the exponential function that satisfies the given conditions:

Initial value = 35, increasing at a rate of 10% per year (1 point)

  1. f(t) = 35 ⋅ 10t
  2. f(t) = 35 ⋅ 1.1t
  3. f(t) = 10 ⋅ 1.1t
  4. f(t) = 35 ⋅ 0.1t
A

2. f(t) = 35 ⋅ 1.1t​

29
Q

The decay of 192 mg of an isotope is given by A(t)= 192e-0.015t, where t is time in years. Find the amount left after 55 years.Round your answer to the nearest whole number. (1 point)

  1. 83
  2. 84
  3. 42
  4. 189
30
Q

Evaluate the logarithm. (1 point)

log5(1/25)

31
Q

Assuming all variables are positive, use properties of logarithms to write the expression as a sum or difference of logarithms or multiples of logarithms. (1 point)

32
Q

Use the product, quotient, and power rules of logarithms to rewrite the expression as a single logarithm. Assume that all variables represent positive real numbers. (1 point)

2log x + 5log y

  1. log( 2x + 5y)
  2. log( 10xy)
  3. log (x2y5)
  4. log(x2 + y5)
A

3. log (x2y5)

​

33
Q

Decide if the function is an exponential function. If it is, state the initial value and the base. (5 points)

y = - 9.3 ⋅ 7x

  1. Exponential Function; base = 7; initial value = - 9.3
  2. Exponential Function; base = - 65.1; initial value = 1
  3. Not an exponential function
  4. Exponential Function; base = x; initial value = - 9.3
A

1. Exponential Function; base = 7; initial value = - 9.3

34
Q

Compute the exact value of the function for the given x-value without using a calculator. (5 points)

f(x) = (1/5)x for x = -1

  1. -5
  2. 5
    • 1/5
  4. 1/5
35
Q

Decide whether the function is an exponential growth or exponential decay function, and find the constant percentage rate of growth or decay. (5 points)

f(x) = 2063 ⋅ 0.9953x

  1. Exponential decay function; -0.47%
  2. Exponential decay function; 0.0047%
  3. Exponential growth function; 0.0047%
  4. Exponential growth function; -0.47%
A
  1. Exponential decay function; -0.47%
36
Q

Find the exponential function that satisfies the given conditions:

Initial value = 56, decreasing at a rate of 0.42% per week (5 points)

  1. f(t) = 56 ⋅ 1.42t
  2. f(t) = 56 ⋅ 0.9958t
  3. f(t) = 56 ⋅ 1.0042t
  4. f(t) = 0.42 ⋅ 0.44t
A

2. f(t) = 56 ⋅ 0.9958t

37
Q

Evaluate the logarithm. (5 points)
log9 (1/81)

38
Q

Find the exact solution to the equation. (5 points)

7-log2(x+5) = 6

  1. x = 3
  2. x = 7
  3. x = -3
  4. x = -6
39
Q

Find the exact solution to the equation. (5 points)

100 (1/5)x/4 = 4

  1. x = 1/2
  2. x = 8
  3. x = 2
  4. x = 9
40
Q

How can exponential functions be reflected over the x-axis?

A

Replace x with -x

41
Q

What exponential transformations occur?

A
  • Constant to an argument → move horizontal curve
  • Constant complete function → change vertical position
42
Q

What is the Natural Base e?

A

A convenient choice for a base is the irrational number

e ~ 2.71828

Natural exponential function: f(x) = ex

= (1 + 1/x)x

= e

43
Q

What is the formula for compound interest?

A

A = P (1 + r/n)nt

A = final balance

P = initial investment

r = interest rate (decimal)

n = number of compoundings in each year

t = time in years

44
Q

What is the formula for continuous compound interest?

45
Q

What is Exponential Growth and Decay?

A

Exponential Growth: y = aeb*x (b > 0)

Exponential Decay: y = ae-b*x (b > 0)

46
Q

What is the exponential population model?

A

P(t) = P(1+r)t

r → constant percentage rate

r > 0: Growth

r < 0: decay

P → initial population

t → time (years)

47
Q

What is the Logistics Growth Model?

A

y = a/(1 + be-(x-c)/d)

48
Q

What is the difference between the domain and range for exponential and logarithmic functions?

A

Exponential Function

  • Domain: all real numbers
  • Range: y > 0

Logarithmic Function

  • Domain: x > 0
  • Range: all real numbers

Switched? inverses

49
Q

What are the Properties of Common Logarithms?

A
  1. log a1 = 0 because a0 = 1
  2. log aa = 1 because a1 = a
  3. log a ax = x because ax = ax
  4. If log ax = log ay, then x = y
50
Q

Properties of Natural Logarithms:

A

LN 1 = 0 because e0 = 1.

LN e = 1 because e1 = e

LN ex = x because ex = ex

If LN x = LN y, then x = y

51
Q

What is the change the base formula?

A

logax = logbx/logba

52
Q

Equality Property:

A

log a un = n log au

53
Q

Product and Quotient Property of Logarithms:

A

Multiplication. If two or more logarithmic expressions with the same base are added, multiply the arguments to find the sum.

log b x + log b y = log b xy

Division. If two or more logarithmic expressions with the same base are subtracted, divide the first argument by the second argument to find the difference. This is called the Quotient Property of Logarithms.

log b x - log b y = log b x÷y

Honors Pre-Calculus (5 decks)

Brainscape helps you reach your goals faster, through stronger study habits.
© 2025 Bold Learning Solutions. Terms and Conditions