Module 01: Functions and their Graps Flashcards
(43 cards)
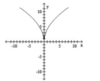
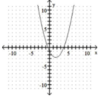
Determine whether the graph is the graph of a function. (2 points)
Yes
No
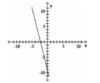
Yes
Determine the domain of the function. (2 points)
f(x) = √(11 - x)
- All real numbers except 11
- x > 11
- All real numbers
- x ≤ 11
4. x ≤ 11
Determine the domain of the function. (2 points)
f(x) = √(x+3) / [(x+8)(x-2)]
- All real numbers except -8, -3, and 2
- x ≥ 0
- All real numbers
- x ≥ -3, x ≠ 2
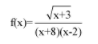
4. x ≥ -3, x ≠ 2
Find the range of the function. (2 points)
f(x) = (x + 5)2 + 8
- y > -8
- y ≥ 8
- y > 8
- All real numbers
2. y ≥ 8
Determine whether the formula describes y as a function of x. Explain your reasoning. (2 points)
y = -3x2 - 7x - 6
The formula “y as a function of x” means that y is the dependent variable; it depends on the independent variable (x) for its value. Therefore, the value of x will directly determine the value of y. Furthermore, if y is a function of x, then it should be able to function as a function, meaning y = -x should also be able to be written as f(x) = -x. When you look at the equation in terms of function notation, it is easier to see how y is a product of x, because whatever value is substituted for x will be equal to y.
If you look at the function when it is graphed, you will see that there is only one y output for each consecutive x value, meaning that it is a function. For example, when x = 6, f(6) = -3(6)2-7(6)-6, there is only one answer, (, -156), and the same applies for any other x value there will only be one y output. Therefore, this is a function.
Determine the intervals on which the function is increasing, decreasing, and constant. (3 points)
- Increasing x < 0; Decreasing x > 0
- Increasing x > 0; Decreasing x < 0
- Increasing x < 3; Decreasing x > 3
- Increasing x > 3; Decreasing x < 3
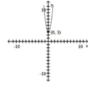
2. Increasing x > 0; Decreasing x < 0
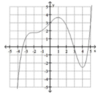
Use the graph of f to estimate the local maximum and local minimum. (2 points)
- No local maximum; local minimum: approx. (1,-7.67)
- Local maximum: (-2,8); local minima: (-3,0) and (3,3)
- Local maximum: approx. (1,8.08); local minima: approx. (-2,-7.67) and (3,2.75)
- Local maximum: ∞ local minima: (-3,0) and (3,3)

3. Local maximum: approx. (1,8.08); local minima: approx. (-2,-7.67) and (3,2.75)
Determine algebraically whether the function is even, odd, or neither even nor odd. (2 points)
f(x) = -3x4 - 2x - 5
- Neither
- Even
- Odd
- Neither
Why is this function, f(x) = x2 + 6, an even function?
If the function is even, changing the x variables to be negative should result in the function being the same as it started as. In comparison, if the function is odd, changing the x variables to be negative, will result in the function being opposite of how it started.
Therefore, to prove that f(x) is an even function, f(-x) should still be equal to x2 + 6.
f(-x)=(-x)2+6
f(-x)=(x)2+6
According to this, f(-x) = f(x), meaning that the function is indeed an even function; furthermore, since the constant in the function - namely 6 - is an even number, the function is definitely even.
f(x) = 2x + 6, g(x) = 4x2
Find (f + g)(x). (1 point)
- 8x3 + 24x
- (2x+6)/4x2
- 4x2 + 2x + 6
- -4x2 + 2x + 6
3. 4x2 + 2x + 6
f(x) = 4x + 7, g(x) = 3x2
Find (f + g)(x). (1 point)
- 3x2 + 4x + 7
- -3x2 + 4x + 7
- (4x+7)/3x3
- 12x3 + 21x
- 3x2 + 4x + 7
f(x) = 4x + 6, g(x) = 2x2
Find (fg)(x). (1 point)
- 8x3 + 12x2
- 2x2 + 4x + 6
- 8x + 12
- 8x2 + 12x
- 8x3 + 12x2
f(x) = 4x + 7, g(x) = 3x2
Find (fg)(x). (1 point)
- 12x2 + 21x
- 3x2 + 4x + 7
- 12x3 + 21x2
- 12x + 21
3. 12x3 + 21x2
f(x) = 5x + 3; g(x) = 6x - 5
Find f/g. (1 point)

3
f(x) = 3x + 2; g(x) = 3x - 5
Find f/g. (1 point)

2
f(x) = √x+9 ; g(x) = 8x - 13
Find f(g(x)). (1 point)
- f(g(x)) = 2 √(2x-1)
- f(g(x)) = 8 √(x-4)
- f(g(x)) = 2 √(2x+1)
- f(g(x)) = 8√(x+9) - 13
- f(g(x)) = 2 √(2x-1)
f(x) = √x+7 ; g(x) = 8x - 11
Find f(g(x)). (1 point)
- f(g(x)) = 2 √(2x+1)
- f(g(x)) = 8 √(x+7) - 11
- f(g(x)) = 8 √(x-4)
- f(g(x)) = 2 √(2x-1)
4. f(g(x)) = 2 √(2x-1)
Find f(x) and g(x) so the function can be expressed as y = f(g(x)).
y = 8x2 + 4
- f(x)=x+4
- g(x)=8x2
Find f(x) and g(x) so the function can be expressed as y = f(g(x)). (1 point)
y = 2/x2+ 3
- f(x) = x + 3
- g(x) = 2/x2
Find the inverse of the function.
f(x) = 5x + 6 (2 points)
f-1 (x) = (x-6)/5
Find the inverse of the function.
f(x) = x3 - 4
f-1(x) = 3√x+4
Find the inverse of the function.
f(x) = 4x3 - 7
f-1(x) = 3√[(x+7)/(4)]
Determine if the function is one-to-one. (2 points)
- Yes
- No
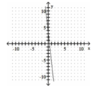
Yes