Maxima and Minima

Question 1

Relative/Local maximum or minimum

Answer 1

Means that the curve has a horizontal tangent line at that piont, but it is not the highest or lowest value that the function attains.

Question 2

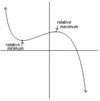
Absolute maximum or minimum

Answer 2

Occurs either at an artificial point or an end point.

Question 3

If a function has a critical value at x=c, then how do you tell whether it is a relative maximum or a relative minimum?

Answer 3

Relative maximum if ƒ”(c) < 0

Relative minimum if ƒ”(c) > 0

Question 4

To determine maximum or minimum,

The technique is always the same:

Answer 4

(a) Take the derviative of the equation.
(b) Set it equal to zero – critical points.
(c) Use the second derivative test:

• (–) = maximum
• (+) = minimum.

Question 5

How do you know when a curve is rising, falling, or at a critical point?

Answer 5

When ƒ’(x) > 0, the curve is rising.

When ƒ’(x) < 0, the curve is falling.

When ƒ’(x) = 0, the curve is at a critical point.

Question 6

How do you know when the curve is concave up, concave down, or at a point of inflection?

Answer 6

When ƒ”(x) > 0, the curve is concave up.

When ƒ”(x) < 0, the curve is concave down.

When ƒ”(x) = 0, the curve is at a point of inflection.

Question 7

How do you find the y-coordinates of a critical point?

Answer 7

Plug the x-value of each critcal point into the original equation.

Question 8

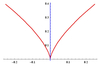
Finding a cusp

Answer 8

lim_x→c- ƒ(x) = ∓∞ and lim_x→c⁺ ƒ(x) = ±∞,

and ƒ(x) is continuous at x=c,

then the curve has a cusp at that point.

Question 9

Finding a horizontal asymptote

A line y = c is a horizontal asymptote of the graph of y = ƒ(x) if:

Answer 9

lim_x→∞ ƒ(x) = c or if lim_x→-∞ ƒ(x) = c

Question 10

Finding a vertical asymptote

A line x = k is a vertical asymptote of the graph of y = ƒ(x) if:

Answer 10

lim_{x→k^{<span>+</span>}} ƒ(x) = ±∞ or if lim_x→k^- ƒ(x) = ±∞