Area and Volume of a Solid of Revolution

Question 1

Vertical Slices

If a region is bounded by ƒ(x) above and g(x) below at all points of the interval [a, b], then the area of the region is given by:

Answer 1

∫_a^b [ƒ(x) – g(x)]dx

Question 2

Horizontal slices

If a region is bounded by ƒ(y) on the right and g(y) on the left at all points of the interval [c, d], then the area of the region is given by:

Answer 2

∫_c^d [ƒ(y) – g(y)]dy

Question 3

Disk method (revolved around x-axis)

In a region whose area is bounded by the curve y = ƒ(x) and the x-axis on the interval [a, b], each disk has a radius ƒ(x), and…

The area of each disk will be:

The volume of the region will be:

Answer 3

π [ƒ(x)]²

π∫_a^b [ƒ(x)]² dx

Question 4

Washer method (revolved around x-axis)

In a region whose area is bounded above by the curve y = ƒ(x) and below by the curve y = g(x), on the interval [a, b], then…

Each washer will have an area of:

A volume of:

Answer 4

π [ƒ(x)² – g(x)²]

π∫_a^b [ƒ(x)² – g(x)²] dx

Question 5

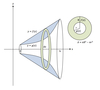
Cylindrical shells method (rotated around y-axis)

If a region whose area is bounded above by the curve y = ƒ(x) and below by the curve y = g(x), on the interval [a, b], then each cylinder will have…

a height of:

a radius of:

a volume of:

Answer 5

• Height = ƒ(x) – g(x)
  
  • ​Or larger value – smaller value
• Radius = x
  
  • Or x – a, if rotated around x = a
  • Or Difference between x values
• Volume = 2π ∫_a^b x[ƒ(x) – g(x)] dx

Question 6

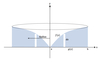
Volume of solid with known cross-sections

Answer 6

If A(x) is the area of a cross section of a solid and A(x) is continuous on [a, b], then the volume of the solid from x = a to x = b is:

V = ∫_a^b A(x) dx