Derivatives Flashcards
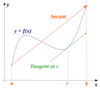
The Difference Quotient
(slope of the secant line)
( ƒ(x1 + h) – ƒ(x1) ) / h
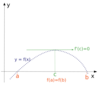
The definition of the derivative
(the slope of the tangent line)
ƒ’(x1) =
limh→0 ( ƒ(x1 + h) – ƒ(x1) ) / h
d/dx [u•v]
(The Product Rule)
u’ • v + v’ • u
d/dx [u/v]
(The Qutient Rule)
(u’ • v - v’ • u) / v2
d/dx ƒ(g(x))
(The Chain Rule)
ƒ’(g(x)) • g’(x)
If y = y(v) and v = v(x), then dy/dx =
dy/dx = dy/dv • dv/dx
d/dx [ku]
(k = constant, u = variable)
k • du/dx
d/dx [k]
0
d/dx k/u
-k / u2 du/dx
d/dx k√u
k / ( 2 √u ) du/dx
d/dx [au]
au • ( ln(a) ) du/dx
d/dx eu
eu du/dx
d/dx [ln u]
1 / u du/dx
d/dx [logbu]
1 / ( u ln(b) ) du/dx
d/dx [sin(u)]
cos(u) du/dx
d/dx [cos(u)]
-sin(u) du/dx
d/dx [tan(u)]
sec2(u) du/dx
d/dx [cot(u)]
-csc2(u) du/dx
d/dx [sec(u)]
sec(u) • tan(u) du/dx
d/dx [cscu]
-cscu•cotu du/dx
d/dx [sin-1(u)]
1 / √ ( 1 – u2 ) du/dx
d/dx [cos-1 (u)]
-1 / √ ( 1 – u2 ) du/dx
d/dx [tan-1(u)]
1 / ( 1 + u2 ) du/dx
d/dx [cot-1(u)]
-1 / ( 1 + u2 ) du/dx
d/dx [sec-1(u)]
1 / ( |u| √( u2 – 1) ) du/dx
d/dx [csc-1(u)]
-1 / ( |u| √( u2 – 1) ) du/dx
The derivative of an inverse function
d/dx ƒ-‘(x)|x=c =
1 / [d/dy ƒ(y)] x=a
Parametric equations
dy/dt / dx/dt =
dy/dx
Formula for differentials
ƒ(x+△x) ≈ ƒ(x) + ƒ’(x)•△x
d2y / dx2 = ?
Second derivative of a parmetric function.
( x’ y” – x” y’ ) / (x’)3
Mean value theorem
For any function that is continuous on [a, b] and differentiable on (a, b) there exists some c in the interval (a, b) such that the secant joining the endpoints of the interval [a, b] is parallel to the tangent at c.
ƒ’(c) = ƒ(b)–ƒ(a)/b–a
Rolle’s theorem
If a real-valued function ƒ is continuous on a closed interval [a, b], differentiable on the open interval (a, b), and f(a) = f(b), then there exists a c in the open interval (a, b) such that
ƒ’(c) = 0
