Continuity Flashcards
1
Q
In order for a function ƒ(x) to be continuous at a point x = c, it must fulfill all three conditions
A
Condition 1: ƒ(c) exists
Condition 2: limx→c ƒ(x) exists
Condition 3: limx→cƒ(x) = ƒ(c)
2
Q
Jump discontinuity
A
limx→a- ƒ(x) ≠ limx→a+ ƒ(x)
3
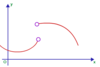
Q
Point discontinuity
A
limx→a ƒ(x) ≠ ƒ(a)

4
Q
Removable discontinuity
A
Occurs when you have a rational expression with common factors in the numerator and denominator. Because these can be canceled, the discountinuity is “removable.”

5
Q
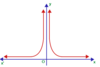
Essential discontinuity
A
Occurs when the curve has a vertical asymptote.