Materials Flashcards
define Hooke’s law
the extension of an object is directly proportional to the force provided it hasn’t been extended beyond its elastic limit
on a graph, how do you know where the elatic limit is?
when the graph is no longer a straight line
if a spring obeys Hooke’s law, does it behave elastically or plastically?
elastically
if a spring is beyond Hooke’s law, does it behave elastically or plastically?
plastically
explain the meaning of elasticity
the object (e.g. the spring) return to its original state when the force is removed
explain the meaning of plasticity
the object will not return to its original state when the force is removed - it stays deformed
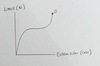
what does Hooke’s law look like graphically?
A is the elastic limit so the line is no longer straight afterwards
give an example of an everyday object that behaves elastically
hairband
give an example of an everyday object that behaves plastically
bluetac
over which range does the spring obey Hooke’s law?
summarise the characteristsics of the graph
range = 0N - 33N
elastic limit = A at 33N
until point A the graph is directly proportional: as the load increases, the extension increases in a proportional manner
after point A, the graph abandons the straight line and becomes curved
sketch a graph showing a single spring, a two springs in series and a two parallel springs being extended
A = single spring being extended
B = series spring being extended
C = parallel spring being extended
if a single spring (A) being extended has a gradient of 0.250 N/cm then calculate the gradient of two springs in series (B) and two parallel springs (C) being extended
A (single) = 0.250 N/cm
B (series) = 0.125 N/cm
C (parallel) = 0.500 N/cm
what is another word for strength of a spring?
stiffness
describe the relationship of A
gradient of A = 0.250 N/cm
as the load increases, the extension increases in a directy proportionally manner
the graph is linear with a straight line through the origin (directly proportional) with a gradient of 0.250 N/cm until point x where the extension increases more than the load increases
A obeys Hooke’s law as force and extension are directly proportional
however, it does not obey Hooke’s law at point x and beyond
describe the relationship of B
compare it to to A
gradient of A = 0.250 N/cm
gradient of B = 0.125 N/cm
in proportion to A, B’s gradient is halved (0.125 N/cm)
two springs in series are half the strength of a single spring
B’s graph is linear with a straight line through the origin showing it is directly proportional
B obeys Hooke’s law as the load (force) increases as the extension increases in a directly proportional manner
describe the relationship of C
compare it to to A
gradient of A = 0.250 N/cm
gradient of C = 0.500 N/cm
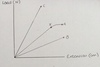
in proportion to A, C’s gradient is doubled (0.500 N/cm)
two parallel springs are double the strength of a signle spring
C’s graph is linear with a straight line through the origin showing it is directly proportional
C obeys Hooke’s law as the load (force) increases as extension increases in a directly proportional manner
rank the springs in order of strength (strongest first, weakest last)
C
A
B
on a Hooke’s law graph, the steeper the gradient, the … the spring
on a Hooke’s law graph, the steeper the gradient, the stronger the spring
D is an elastic band
describe the elastic band by referring to the graph
D does not obey Hooke’s law as its gradient is not directly proportional
the elastic band is strong (steep gradient), then weak (flat graident), then strong again
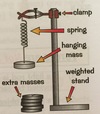
draw a clear diagram of the equipment used in an experiment investing Hooke’s law on a single spring
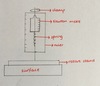
select equipment for investigating Hooke’s law on a single spring
The experiment is set up as shown. A retort stand is attached to a clamp holding a Newton metre which is holding a spring. Another clamp holds a ruler. The spring is pulled down (extended). Each time the spring is extended one centimetre further. The load is recorded after each extension using the Newton metre.
control variable = the surface the experiment is carried out on
independent variable = the extension of the spring, measured by a ruler in cm
dependent variable = the load on the spring, measured by a Newton metre in Newtons (N)
how do you calculate the extension of a spring?
extension of spring = extended length — original length
how do you incur systematic error when investing Hooke’s law?
not zeroing the Newton metre horizontally
can you improve systematic error?
no, but you can calculate the systematic error and then subtract it from each reading and continue accordingly
how can you improve parallax error when reading a Newton metre?
ensure that you are eye level with the equipment and filming yourself so you can clearly see
Look at Experimental Write-Up of Hooke’s Law
What should a load/extension graph that obeys Hooke’s law look like?
As extension increases, load increases
The line of best fit should go through he origin, being directly proportional and obeying Hooke’s law
At the end of our graph there is a curve as the spring stops behaving elastically and started behaving plastically which means that the extension increased more than the load increased
How do you investigate Hooke’s law with a spring?
- Set up the apparatus. Make sure you have plenty of extra masses and measure the weight of each (with a balance)
- Measure the length of the spring (e.g. with an accurate mm ruler) when no load is applied. Ensure the ruler is vertical (e.g. set square) and measure the spring at eye level. (This is the spring’s natural level)
- Add one mass at a time and allow the spring to come to rest, then measure the new length of the spring. The extension is the change in the length from the original length. Adding a marker to the top and bottom of the spring might make measuring lengths easier. Repeat this process until you have enough measurements (no fewer than 6)
- Once you’re done, repeat the experiment and calculate an average value for the length of the spring for each applied weight. This will make your results reliable
