K7 DB-Zugriffsverfahren Flashcards by Li Th

GDB K7 DB-Zugriffsverfahren

Übersicht Zugriffsverfahren

How well did you know this?

Not at all

Perfectly

GDB K7 DB-Zugriffsverfahren

Listen: Sequentielle Listen auf Externspeichern

Prinzip: Zusammenhang der Satzmenge wird durch physische Nachbarschaft hergestellt
Reihenfolge der Sätze: ungeordnet (Einfügereihenfolge) oder sortiert nach einem oder mehreren Attributen (sog. Schlüssel)
wichtige Eigenschaft: Cluster-Bildung, d. h., physisch benachbarte Speicherung von logisch zusammengehörigen Sätzen
Sequentielle Listen garantieren Cluster-Bildung in Seiten für die Schlüssel-/Speicherungsreihenfolge
pro Satztyp kann Cluster-Bildung nur bezüglich eines Kriteriums erfolgen, falls keine Redundanz eingeführt werden soll

How well did you know this?

Not at all

Perfectly

GDB K7 DB-Zugriffsverfahren

Listen: Gekettete Listen auf Externspeichern

Prinzip: Verkettung erfolgt zwischen Datensätzen
Speicherung der Sätze i. Allg. in verschiedenen Seiten
Seiten können beliebig zugeordnet werden
Mehrfachverkettung nach verschiedenen Kriterien (Schlüsseln) möglich

How well did you know this?

Not at all

Perfectly

GDB K7 DB-Zugriffsverfahren

Hashing auf Externspeichern

Hash-Adresse bezeichnet Bucket (Behälter, Seite)

Das Kollisionsproblem wird dadurch entschärft, dass mehr als ein Satz auf seiner Hausadresse gespeichert werden kann.
Aufnahme von bis zu b Sätzen (b = Bucket-Kapazität)
Primärbereich kann bis zu b*m Sätze aufnehmen !

Überlaufbehandlung

Überlauf tritt erst beim (b+1)-ten Synonym auf
viele (bekannte) Verfahren sind möglich, aber lange Sondierungsfolgen im Primärbereich sollten vermieden werden häufig Wahl eines separaten Überlaufbereichs mit dynamischer Zuordnung der Buckets
Optionen: Verkettung der Überlauf-Buckets pro Primär-Bucket oder Zuordnung von Überlauf-Buckets zu mehreren Primär-Buckets

Speicherungsreihenfolge im Bucket

ohne Ordnung (Einfügefolge)
nach der Sortierfolge des Schlüssels: aufwendiger, jedoch Vorteile beim Suchen (sortierte Liste!)

Bucket-Größe

Bucket-Adressierung eignet sich besonders gut für die Anwendung auf Externspeichern
Wahl der Bucket-Größe: meist Seite (Transfereinheit)
Zugriff auf die Hausadresse bedeutet dann eine physische E/A; jeder weitere Zugriff auf ein Überlauf-Bucket löst jeweils einen weiteren physischen E/A-Vorgang aus.

How well did you know this?

Not at all

Perfectly

GDB K7 DB-Zugriffsverfahren

Allgemeine Bäume

How well did you know this?

Not at all

Perfectly

GDB K7 DB-Zugriffsverfahren

Implementierung von allgemeinen Bäumen

How well did you know this?

Not at all

Perfectly

GDB K7 DB-Zugriffsverfahren

m-Wege-Suchbäume

How well did you know this?

Not at all

Perfectly

GDB K7 DB-Zugriffsverfahren

Knotenformat eines m-Wege-Suchbaums

How well did you know this?

Not at all

Perfectly

GDB K7 DB-Zugriffsverfahren

Aufbaubeispiel m-Wege-Suchbäume

How well did you know this?

Not at all

Perfectly

GDB K7 DB-Zugriffsverfahren

Beobachtung zu m-Wege-Suchbäume

Die Schlüssel in den inneren Knoten besitzen zwei Funktionen. Sie identifizieren Daten(sätze) und sie dienen als Wegweiser in der Baumstruktur.

Der m-Wege-Suchbaum ist im allgemeinen nicht ausgeglichen. Es ist für Aktualisierungsoperationen kein Balancierungsmechanismus vorgesehen. (schlechte Platzausnutzung, Entartung)

How well did you know this?

Not at all

Perfectly

GDB K7 DB-Zugriffsverfahren

Wichtige Eigenschaften von m-Wege-Suchbäumen

Die D_i können Daten oder Zeiger auf die Daten repräsentieren. Zur Vereinfachung werden die D_i (in den Illustrationen) weggelassen.
S(P_i) sei die Seite, auf die P_i zeigt, und K(P_i) sei die Menge aller Schlüssel, die im Unterbaum mit Wurzel S(P_i) gespeichert werden können.

How well did you know this?

Not at all

Perfectly

GDB K7 DB-Zugriffsverfahren

Kostenanalyse für m-Wege-Suchbäume: Die Anzahl der Knoten N in einem vollständigen Baum der Höhe h ist…

How well did you know this?

Not at all

Perfectly

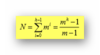
GDB K7 DB-Zugriffsverfahren

Kostenanalyse für m-Wege-Suchbäume: bei voller Belegung ergibt sich als Anzahl der Einträge…

n = N*(m-1)

How well did you know this?

Not at all

Perfectly

GDB K7 DB-Zugriffsverfahren

Kostenanalyse für m-Wege-Suchbäume: im ungünstigsten Fall ist der Baum völlig entartet…

n = N = h

How well did you know this?

Not at all

Perfectly

GDB K7 DB-Zugriffsverfahren

Kostenanalyse für m-Wege-Suchbäume: Schranken für die Höhe eines m-Wege-Suchbaums

How well did you know this?

Not at all

Perfectly

GDB K7 DB-Zugriffsverfahren

Kostenanalyse für m-Wege-Suchbäume: Wartungsaufwand

O(n)

How well did you know this?

Not at all

Perfectly

GDB K7 DB-Zugriffsverfahren

Aufsuchen eines Schlüssels in einem m-Wege-Suchbaum

How well did you know this?

Not at all

Perfectly

GDB K7 DB-Zugriffsverfahren

Durchlaufen eines m-Wege-Suchbaums in symmetrischer Ordnung

How well did you know this?

Not at all

Perfectly

GDB K7 DB-Zugriffsverfahren

Mehrwegbäume

Ziel: Aufbau sehr breiter Bäume von geringer Höhe

in Bezug auf Knotenstruktur vollständig ausgeglichen
effiziente Durchführung der Grundoperationen
Zugriffsverhalten ist weitgehend unabhängig von Anzahl der Sätze
Einsatz als universelle Zugriffs- oder Indexstruktur

Grundoperationen:

Einfügen/Löschen eines Satzes
direkter Schlüsselzugriff auf einen Satz
sortiert sequentieller Zugriff auf mehrere Sätze

Breites Spektrum von Anwendungen

Dateiorganisation (“logische Zugriffsmethode”, VSAM)
Datenbanksysteme (Varianten des B*-Baumes in allen DBVS!)
Text- und Dokumentenorganisation
. . .

How well did you know this?

Not at all

Perfectly

GDB K7 DB-Zugriffsverfahren

B-Bäume: Definition

Seien k, h ganze Zahlen, h ≥ 0, k > 0. Ein B-Baum B der Klasse τ (k,h) ist entweder ein leerer Baum oder ein geordneter Suchbaum mit folgenden Eigenschaften:

Jeder Pfad von der Wurzel zu einem Blatt hat die gleiche Länge h-1.
Jeder Knoten außer der Wurzel und den Blättern hat mindestens k+1 Söhne. Die Wurzel ist ein Blatt oder hat mindestens 2 Söhne.
Jeder Knoten hat höchstens 2k+1 Söhne.
Jedes Blatt mit der Ausnahme der Wurzel als Blatt hat mindestens k und höchstens 2k Einträge.

Reformulierung der Def.:

(4) und (3) ‚Eine Seite darf höchstens voll sein.‘
(4) und (2) Jede Seite (außer der Wurzel) muss mindestens halb voll sein. Die Wurzel enthält mindestens einen Schlüssel.
(1) Der Baum ist, was die Knotenstruktur angeht, vollständig ausgeglichen.

How well did you know this?

Not at all

Perfectly

GDB K7 DB-Zugriffsverfahren

B-Bäume: Einträge

How well did you know this?

Not at all

Perfectly

GDB K7 DB-Zugriffsverfahren

Beispiel: B-Baum der Klasse τ(2,3)

How well did you know this?

Not at all

Perfectly

GDB K7 DB-Zugriffsverfahren

B-Bäume: Höhe, balacierte Struktur

How well did you know this?

Not at all

Perfectly

GDB K7 DB-Zugriffsverfahren

B-Bäume: Einfügen

Einfügealgorithmus (ggf. rekursiv)

suche Einfügeposition;
wenn Platz vorhanden ist, speichere Element, sonst schaffe Platz durch Split-Vorgang und füge ein.

How well did you know this?

Not at all

Perfectly

# GDB K7 DB-Zugriffsverfahren B-Bäume Beispiel: **B-Baum der Klasse τ(2, h), Einfügen** Einfügereihenfolge: _77, 12, 48, 69_, _33_, _89, 97_, 91, 37, 45, 83, 2, 5, 57, 90, 95, 99, 50

# GDB K7 DB-Zugriffsverfahren B-Bäume Beispiel: **B-Baum der Klasse τ(2, h), Einfügen** Einfügereihenfolge: 77, 12, 48, 69, 33, 89, 97, _91_, _37, 45, 83_, 2, 5, 57, 90, 95, 99, 50

# GDB K7 DB-Zugriffsverfahren B-Bäume Beispiel: **B-Baum der Klasse τ(2, h), Einfügen** Einfügereihenfolge: 77, 12, 48, 69, 33, 89, 97, 91, 37, 45, 83, _2_, _5, 57, 90, 95,_ 99, 50

# GDB K7 DB-Zugriffsverfahren B-Bäume Beispiel: **B-Baum der Klasse τ(2, h), Einfügen** Einfügereihenfolge: 77, 12, 48, 69, 33, 89, 97, 91, 37, 45, 83, 2, 5, 57, 90, 95, _99_, 50

# GDB K7 DB-Zugriffsverfahren B-Bäume Beispiel: **B-Baum der Klasse τ(2, h), Einfügen** Einfügereihenfolge: 77, 12, 48, 69, 33, 89, 97, 91, 37, 45, 83, 2, 5, 57, 90, 95, 99, _50_

# GDB K7 DB-Zugriffsverfahren B-Bäume**: Kostenanalyse für Direkte Suche**

* Anzahl der zu holenden Seiten: f (fetch) * Anzahl der zu schreibenden Seiten: w (write)

# GDB K7 DB-Zugriffsverfahren B-Bäume: **Kostenanalyse für Sequentielle Suche**

Durchlauf in symmetrischer Ordnung: f_seq = N Pufferung der Zwischenknoten im HSP wichtig!

# GDB K7 DB-Zugriffsverfahren B-Bäume: **Kostenanalyse für Einfügen**

# GDB K7 DB-Zugriffsverfahren B-Bäume: **Löschen**

Die B-Baum-Eigenschaft muss wiederhergestellt werden, wenn die Anzahl der Elemente in einem Knoten kleiner als k wird. Durch **Ausgleich** mit Elementen aus einer Nachbarseite oder durch **Mischen** (Konkatenation) mit einer Nachbarseite wird dieses Problem gelöst. Beim Ausgleichsvorgang sind in der Seite P k-1 Elemente und in P’ mehr als k Elemente.

# GDB K7 DB-Zugriffsverfahren B-Bäume**: Löschalgorithmus**

# GDB K7 DB-Zugriffsverfahren B-Bäume Beispiel: Löschen

# GDB K7 DB-Zugriffsverfahren B-Bäume: **Kostenanalyse für Löschen**

# GDB K7 DB-Zugriffsverfahren B-Bäume: **Überlaufbehandlung**

# GDB K7 DB-Zugriffsverfahren B-Bäume: **Überlaufbehandlung Einfügekosten bei m=2**

# GDB K7 DB-Zugriffsverfahren B-Bäume: **Verbesserung des Belegungsgrades**

# GDB K7 DB-Zugriffsverfahren B-Bäume: **Speicherplatzbelegung**

# GDB K7 DB-Zugriffsverfahren B-Bäume: **Suche innerhalb einer Seite**

# GDB K7 DB-Zugriffsverfahren B\*-Bäume: **Definition**

Seien k, k\* und h\* ganze Zahlen, h\* ≥ 0, k, k\* \> 0. Ein B\*-Baum B der Klasse τ(k,k\*,h\*) ist entweder ein leerer Baum oder ein geordneter Suchbaum, für den gilt: 1. Jeder Pfad von der Wurzel zu einem Blatt besitzt die gleiche Länge h\*-1. 2. Jeder Knoten außer der Wurzel und den Blättern hat mindestens k+1 Söhne, die Wurzel mindestens 2 Söhne, außer wenn sie ein Blatt ist. 3. Jeder innere Knoten hat höchstens 2k+1 Söhne. 4. Jeder Blattknoten mit Ausnahme der Wurzel als Blatt hat mindestens k\* und höchstens 2k\* Einträge.

# GDB K7 DB-Zugriffsverfahren B\*-Bäume: **2 Knotenformate**

# GDB K7 DB-Zugriffsverfahren B\*-Bäume: **Es gilt für L, k und k\*...**

# GDB K7 DB-Zugriffsverfahren **Beispiel: B\*-Baum der Klasse τ(2, 2, 3)**

# GDB K7 DB-Zugriffsverfahren Erklärungsmodell für den B\*-Baum

Der B\*-Baum lässt sich auffassen als eine gekettete sequentielle Datei von Blättern, die einen Indexteil besitzt, der selbst ein B-Baum ist. Im Indexteil werden insbes. beim Split-Vorgang die Operationen des B-Baums eingesetzt.

# GDB K7 DB-Zugriffsverfahren Grundoperationen beim B\*-Baum: **Direkte Suche**

Da alle Schlüssel in den Blättern sind, kostet jede direkte Suche h\* Zugriffe. h\* ist jedoch im Mittel kleiner als h in B-Bäumen. Da f_avg beim B-Baum in guter Näherung mit h abgeschätzt werden kann, erhält man also durch den B\*-Baum eine effizientere Unterstützung der direkten Suche.

# GDB K7 DB-Zugriffsverfahren Grundoperationen beim B\*-Baum: **Sequentielle Suche**

Sie erfolgt nach Aufsuchen des Linksaußen der Struktur unter Ausnutzung der Verkettung der Blattseiten. Es sind zwar ggf. mehr Blätter als beim B-Baum zu verarbeiten, doch da nur h\*-1 innere Knoten aufzusuchen sind, wird die sequentielle Suche ebenfalls effizienter ablaufen.

# GDB K7 DB-Zugriffsverfahren Grundoperationen beim B\*-Baum: **Einfügen**

Es ist von der Durchführung und vom Leistungsverhalten her dem Einfügen in einen B-Baum sehr ähnlich. Bei inneren Knoten wird die Spaltung analog zum B-Baum durchgeführt. Beim Split-Vorgang einer Blattseite muss gewährleistet sein, dass jeweils die höchsten Schlüssel einer Seite als Wegweiser in den Vaterknoten kopiert werden. Die Verallgemeinerung des Split-Vorgangs lässt sich analog zum B-Baum einführen.

# GDB K7 DB-Zugriffsverfahren Grundoperationen beim B\*-Baum: Beispiel Einfügen

# GDB K7 DB-Zugriffsverfahren Grundoperationen beim B\*-Baum: **Schema Split-Vorgang**

# GDB K7 DB-Zugriffsverfahren Grundoperationen beim B\*-Baum: **Löschen**

Datenelemente werden immer von einem Blatt entfernt (keine komplexe Fallunterscheidung wie beim B-Baum). Weiterhin muss beim Löschen eines Schlüssels aus einem Blatt dieser Schlüssel nicht notwendigerweise aus dem Indexteil entfernt werden; er kann seine Funktion als Wegweiser behalten.

# GDB K7 DB-Zugriffsverfahren Grundoperationen beim B\*-Baum: **Beispiel Löschen**

# GDB K7 DB-Zugriffsverfahren B\*-Bäume: **Optimierungsmöglichkeiten**

# GDB K7 DB-Zugriffsverfahren B\*-Bäume: **Eigenschaften**

# GDB K7 DB-Zugriffsverfahren B- und B\*-Baum: **Quantitativer Vergleich**

# GDB K7 DB-Zugriffsverfahren Zusammenfassung