GMAT Flashcards
What are the 2 top tips for the GMAT?
- Spend extra time on the first 10 questions. They are absolutely crucial
- You are always better off making your best guess ⇒ the best guess can often be determined by which answer option that has the most in common with the rest (the most common answer theorem)
What are the question types in the quantitative test and what share do they account for? (old test)
Data sufficiency questions = 40 %
When are you trying to find a Yes/No answer for data sufficiency questions?
If the question asked starts with “is”, “are” or “does” you look for a yes/no answer rather than a number.
What are integers?
What are whole numbers?
What are irrational numbers?
Numbers that canNOT be expressed as a fraction or ratio.
Examples: π and √2
When do you know that the GMAT is testing you in imaginary numbers?
If they ask you to take any EVEN ROOT OF A NEGATIVE NUMBER.
√-100 or √-8 fx.
What are the prime numbers up until 130
2, 3, 5, 7,
11, 13, 17, 19,
23, 29,
31, 37,
41, 43, 47,
53, 59,
61, 67,
71, 73, 79,
83, 89,
97,
101, 103, 107, 109,
113,
127.
What does “absolute value” mean and how is it expressed?
A number’s absolute value is its distance from zero on the number line, and like any distance, its ALWAYS positive.
Absolute value of 3 is 3. Absolute value of -8 is 8.
What is the order to work in maths?
PEMDAS
Parantheses
Exponents
Multiplication
Division
Addition
Subtraction
What is (x + y)*(x + y)?
(x + y)^2
x^2 + 2xy + y^2
What is (x - y)*(x - y)?
(x - y)^2
x^2 - 2xy + y^2
What is (x + y)*(x - y)?
x^2 - y^2
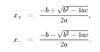
What is
How do you multiply exponent together? fx: x^3 * x^5
X^3 * X^5
Simply add the exponents together: X^3 * X^5 = X^8
is the same as: (x*x*x) * (x*x*x*x*x) = x^3 * x^5 = X^8
How do you divide exponents together? fx: y^3 / y^5
Simply subtract the denominator from the numerator.
y^3 / y^5 = (y3 - y5) = y^-2
What is the value of one exponent raised to another exponent? such as: (x^6)^3
Just multiply the two exponents
(X^6)^3 = x^18
What is 355^0?
1
ALL real numbers raised to the power of 0 = 1
What is x^0?
1
ALL real numbers raised to the power of 0 = 1
What is 3^-4?
which is = 1 / 3^4
which is 1 / 81
What can be said about “any number greater than 1 raised to a negative exponent”?
It will be a number greater than 0 but less than 1.
What is a number raised to a fractional power? such as X^⅙
ALL real numbers raised to the power of 0 = 1
X^⅙ =
What is the result of 2^2, 2^3, 2^4, 2^5, 2^6, 2^7, 2^2, 2^9, 2^10
What is the result of 3^2, 3^3, 3^4, 3^5?
What is the result of 5^2, 5^3, 5^4?
What is the result of 6^2, 6^3?
What is the result of 7^2, 8^2, 9^2, 10^2, 11^2, 12^2, 13^2, 14^2, 15^2, 16^2?
7^2 = 49
8^2 = 64
9^2 = 81
10^2 = 100
11^2 = 121
12^2 = 144
13^2 = 169
14^2 = 196
15^2 = 225
16^2 = 256
What is the difference between a finding the factors of a number and finding the prime factors? The processes?
Factors = all numbers can be used
Prime factors = only prime factors can be used
What is basis points?
It is 1 of 100.
0.45 % = 45 basis points.
What percent is 600 of 200?
300 %
but percentage increase from 200 to 600 is 200%
What is the percentage increase from 300 to 600?
100 %
but 600 is 300 % of 200.
How can you easily simplify a complex fraction? such as 210/2,772
Divide by 2 if possible, then 3, then 5, then 7
(210 / 2) / (2772 / 2) = 105 / 1386
(105 / 3) / (1386/3) = 35 / 462
(35 /7) / (462/7) = 5 / 66
How do you know if a number is divisible by a prime number?
Take the number, fx. 2772
then write it out as 2+7+7+2 = 14
Any prime number going to 14 will work = either 2 or 7.
What are the six main rules to remember in terms of exponents and roots?
Answer:
Question:
Answer:
(3* 7) + (7* 3) = 21 +21 = 42 = D.
Makes sense, since you have 3 / (1 / 7), as 1/7 naturally goes into 1 seven times. And 3 is in the numerator, so it has to go up to three (which is three times as much as 1, i.e. 3 * 7 = 21).
The same logic can be applied for the other part.
Question:
Answer:
64^k is the same as (4^3)^k
So following the rule of multiplying exponents when one exponent is raised to another, we simply have to figure out what:
3* k > 14
k > 14/3
k > 4,67
K must be B = 5.
Question:
answer:
the prime numbers less than 10 are: 2, 3, 5 , 7
2*3 = 6 so cannot be A
Nothing can be multiplied to B as it has to be DISTINCT numbers = B
2*5 = 10
2*7 = 14
3*5 = 15
What are the rules of the cube root table and how does the table look?
- Take the last digit in a number: for example 6 in 636,056 and find that digit in the last digit column.
- Look at the three first digits in a number and find the digit in the table where they do NOT exceed the cube. For example 636 in 636,056.
So cube root of 636,056 would be 86
What are the solutions to the equation x^2 + -2x = 15?
First, re-order to separate 0.
x^2 - 2x - 15 = 0
Now factor (-15)
- 1 and 15 1 and -15
- 3 and 5 3 and -5
Which pair can you manipulate to get to -2?
-1 + 15 = 14 so no
1 -15 = -14 so no
-3 + 5 = 2 so no
3 - 5 = -2 so YES
(x - 3) * (x + 5)
x + 3 = 0, then x = -3
x - 5 = 0, then x = 5
What is the median of 105, 106, 107, 108, 109, 110, 111, 112, 113?
The middle value which in this range of 9 values will be the 5th value = 109.
What is the median of 105, 108, 110, 112, 114, 115?
6 different numbers so the median is the average of the 3rd and 4th number.
(110 + 112) / 2 = 111
What is the mode?
The most common element in a set
NOTE!!! A set can have more than one mode.
NOTE NOTE!!! A set can also NOT have a mode if no number occurs more than once
What is the range?
The difference between the largest and the smallest number.
How is the standard deviation calculated? and how is it useful to know?
The standard deviation is the square root of the result of the summation of the squares of the differences between the individual values of the set and the mean, divided by the number of items in the set.
You will not have to calculate this on the GMAT.
But… you might be asked which set of numbers has the largest standard deviation.
What is the formula for calculating the third side of a right triangle?
A^2 + B^2 = C^2 (pythagoras)
What are parallel lines?
Lines that if extended to infinity, would never intersect.
How do you calculate the area of a triangle?
½ * Base * Height
How do isosceles triangles look and what are their properties?
- Two sides of equal length
- The two angles opposite the sides of equal length are also of equal degree
How do equilateral triangles look and what are their properties?
- All sides of equal length
- All angles have 60 degrees
How do you calculate the area of an equilateral triangle?
(√3 / 4) * s^2
(1. 732 / 4) * s^2
0. 433 * s^2
How do right triangles look and what are their properties?
- One angle is 90 degrees
- The third side (hypotenuse) can be calculated by A^2 + B^2 = C^2
How do right isosceles triangles look and what are their properties?
- one angle with 90 degrees
- Two sides of equal length
What is the 3-4-5 triangle type?
A common ratio used on the GMAT.
RIGHT triangles with the ratio of 3,4 and 5.
- A is 3, B is 4 then C = 5
- A is 6, B is 8, then C = 10
- A is 9, B is 12, then C = 15
- A is 12, B is 16, then C = 20
What is the 5-12-13 triangle type?
A common RIGHT triangle ratio:
- A is 5, B is 12, then C = 13
- A is 10, B is 24, Then C = 26
What is the 30 degrees, 60 degrees and 90 degrees triangle?
The 1 - √3 - 2
- If A is 1, B is √3, then c = 2
- If A is 5, B is 5*√3, then c = 10
- If A is 8, B is 8* √3, then c = 16
What is the perimeter?
How far there is around a triangle, square etc.
The sum of the sides.
How do a rhombus look and what are their properties?
A rhombus is a quadrilateral with sides of equal length and two sets of opposite angles with equal measures.
How do a parallelogram look and what are their properties?
Two sets of parallel lines
The two sets have different length
How do you calculate the area of a parallelogram?
If you recognize that it is simply a square and two triangles of equal size, the calculation simply become
AREA = BASE * HEIGHT
How do trapezoids look and what are their properties?
One pair of parallel lines
The two other sides have equal length but are not parallel
How do you calculate the area of a trapezoid?
Recognize that a trapezoid is a square with two equal triangles.
AREA = HEIGHT * ((A + C) / 2)
Thus we just take the height and the average of the length of the two parallel lines. Then it is essentially just as calculating a rectangle.
How do you calculate the circumference?
The circumference is the distance around a circle (what we call a perimeter in a polygon).
It is simply:
Diameter * π
or: 2 * r * π
What is the area of a circle?
A = r^2 * π
How do you calculate the volume and surface area of a right circular cylinder?
How do you calculate the volume and surface area of a square pyramid?
How do you calculate the volume and the surface area of a cube?
How do you calculate the volume and the surface area of a rectangular solid?
How do you calculate the volume of a general cone/pyramid?
For a right circular cone, you would obviously find A by taking r^2*π
How do you calculate the volume and surface area of a sphere?
What is the result of “even*even”?
Even
4*4 = 16
What is the result of “even*odd”?
Even
4*5 = 20
What is the result of “odd*odd”?
odd
13*13 = 169
What is the result of “even + even”?
Even
22 + 36 = 58
What is the result of “odd + odd”?
Even
17 + 19 = 38
What is the result of “odd + even”?
odd
21 + 22 = 43
What is the result of “negative * negative”?
Positive
-4 * -5 = 20
What is the result of “positive * negative”?
Negative
5 * -6 = -30
What is the result of “positive + negative”?
It depends.
on which one is biggest.
When an odd number is raised to an exponent, what will it result in?
It will still be an ODD number.
13*13 = 169.
No matter if it is raised to 2, 3, 4, 5, 6 etc., it will always be an odd number
When an even number is raised to an exponent, what will it result in?
It will still be an EVEN number.
12*12 = 144.
No matter if it is raised to 2, 3, 4, 5, 6 etc., it will always be an even number
What is the result of “non-integer * non-integer”?
It will always be a NON-INTEGER
0.5 * 0.5 = 0.25.
What is the result of “integer * non-integer”?
It depends.
What is the key component of combinatorial math and what is the formula used?
Factorials.
n! = n* (n - 1) * (n- 2) * - (n - 3) * ….
So
- 2! = 2* 1 = 2
- 3! = 3 * 2 * 1 = 6
- 4! = 4 * 3 * 2 * 1 = 24
- 5! = 5 * 4 ‘ 3 * 2 *1 = 120
- 6! = 6* 5 * 4* 3 * 2 ‘ 1 = 720
- 7! = 7 * 6 * 5 * 4 * 3 * 2 * 1 = 5,040
What is the formula for combinations and what does combinations refer to?
Combinations regards groupings where ORDER DOES NOT MATTER
What is the formula for permutations and what does permutations refer to?
Permutation regards groupings where ORDER MATTERS.
How do you multiply fractions? for example 4/9 x 3/2?
4/9 * 3/2
4*2 / 9*2 = 12/18 = 2/3
What should you ask yourself for inference questions?
- If the statements in the passage are true, what else has be true?
- When having found potential answers, ask yourself “what if the opposite of this answer were true?”
ALWAYS Pick the moderate statement over the extreme.
What are the three main ways in which an answer can be wrong for sentence correction questions?
It violates a rule of grammar
It is worded in an unclear way
It is worded in a “nonstandard” way; i.e. it sounds funny
Which words should you look for to avoid being trapped by pronouns errors?
- He
- She
- It
- they
- them
Ask yourself whether
- is it clear who the referent is?
- is it the right pronoun for that referent?
What are some of the most frequent quantity-words used in the GMAT?
What are some of the most frequent countable/non-countable words used in the GMAT?
Countable words should be used when you can normally assign a whole number to it. Such as six cars.
Non-countable items are for example a little soup as you cannot quantify “a little soup”.
A cup of soup, of course, would be countable = 1.
What is the most common error in sentence correction questions?
No error at all.
20 % has no errors at all.
What are 3 points that should raise an alarm for sentence correction questions?
A sentence does not have to be wrong when it includes any of the following but it often will be:
- Any answer that includes “being”
- Passive verb forms when active verbs would work just as well
- Words ending in “-ing” when there are simpler choices
If you have to give your best guess for sentence correction questions, which two rules should you follow?
- Pick the shortest answer
- Pick the “most common” answer.
- The one that has the most in common with the other options
What are good examples of phrases in which the writer CONTINUES his/her line of thought?
What are good examples of phrases in which the writer CHANGEs his/her line of thought?
How should your essay outline ideally look?
- Paragraph 1: INTRODUCTION
- State argument in a clear statement
- Acknowledge that the opposite position has merits, but that for the following X reasons (summarize your points), my position is the correct one
- Paragraph 2: REASON 1, with supporting evidence/examples/facts
- Paragraph 3: REASON 2, with supporting evidence/examples/facts
- Paragraph 4: REASON 3, with supporting evidence/examples/facts
- Paragraph 5: CONCLUSION
- For the X reasons previously stated, my argument is the correct one
- The argument would have been more persuasive if it ______.
What does bisect mean?
Divide (a line, angle, or shape) into TWO EXACTLY EQUAL parts.
XB bisects ABY only if it splits ABY into two exactly equal parts, meaning that there must be a 45 degree angle on both sides (given that ABY is a 90 degree angle).
How can you derive the side of a square from its diagonal?
The side of a square is it’s diagonal divided by 2 (derived from pythagoras)
How do you quickly add to fractions with different denominators?
Multiply the numerator of the first fraction with the denominator of the second fraction, which is equal to the numerator of the new fraction.
The same applies for the second part, multiply the numerator of the second fraction with the denominator of the first fraction, which is equal to the numerator of the new second fraction.
Lastly, you multiply the two denominators, which is equal to the new common denominator for the two new fractions.
Now you can just add them together normally.
How do you quickly subtract two fractions with different denominators?
Same methods as how you add them, you just subtract instead when you get the common denominator.
How do you multiply two fractions?
How do you divide a number (or fraction) with a fraction?
What does “place value” refer to?
What are inequalities in math?
Statements that involve “<” or “>”.
What is a “perfect square”?
What is a “perfect cube”?
What is LCD and what is the LCD of two numbers?
What are the results of (-3)^2 and -3^2 ?
(-3)^2 = -3 * -3 = 9
-3^2 = - 3*3 = - 9
How can you simplify exponent expression so they are easier to work with?
For negative exponents, you can always divide that expression by one and change the negative exponent to a positive.
Also, you can always move exponents from the numerator to denominator or vice versa by changing the sign.
- = 1 / 2^3 = 1 / 8
- ) (3^3 * 1) / 1 = 9 / 1 = 9
When do you make ADDITION and when do you make MULTIPLICATION of exponents?
How do you add or subtract terms when the bases are different? (working with exponents)
How can you rewrite the √5^12 ?
How do you multiply and divide square roots?
What should you do when you get to a result that is not an answer option when working with square root results such as √50 or √12?
How do you ADD or SUBTRACT under the square root symbol?
Do NOT get confused or fall in the trap of using the rules from multiplication and division under the square root symbol.
Instead…
What is 7^6 * 7^9?
7^15
when multiplying roots you can just add the roots together (when the base is the same)
What is (a^3)^2?
A^6
when multiplying roots you can just add the roots together (when the base is the same)
What is (3^2)^-3 ?
3^-6
What is 5^5 / 5^3?
5^2 = 25
When dividing roots, you can subtract them as long as the base is the same
What is 11^4 / 11^x ?
11^(4-x)
what is (5^2)^x ?
25^x OR 5^2*x
what is (5^6 * 5^4x) / 5^4 ?
We can simplify to:
5^2 * 5^4x
And then simplify to:
5^(4x + 2)
What is y^7 * y^8 * y^-6?
y^7+8-6 = y^9
What is y^4 / y^-3?
Y^(4-(-3) = y^7
What is (3^2x * 3^6x) / 3^-3y?
3^8x / 3^-3y
3^8x + 3^3y OR …. 3^(8x + 3y)
What is 27^⅓ + 9^½ + (3/9^0)
3 + 3 + 3/1 = 9
What is -3^4?
-3 * -3 * -3 * -3 = -81
Which of the following 5 options are equal to (⅖)^-3?
- -(⅔)^3
- (⅖)^⅓
- (- ⅖ )^3
- (5/2)^⅓
- (5/2)^3
The answer is option 5 such that (⅖)^-3 = (5/2)^3.
You can shift around the numerator and denominator IF you also change the plus/minus sign in the root.
What is 8^3 * 2^6?
(2^3)^3 * 2^6
2^9 * 2^6
2^9+6
2^15
What is 25^4 * 125^3?
(5^2)^4 * (5^3)^3
5^8 * 5*9
5*17
What is 9^-2 * 27^2?
(3^2)^-2 * (3^3)^2
3^-4 * 3^6
3^-4+6
3^2
9
What is 6^3 + 3^3?
6^3 + 3^3
(2 * 3)^3 + 3^3
2^3 * 3*3 + 3*3
3^3 (2^3 + 1)
3^3 (9)
3^3 (3^2)
3^5
What is (4^8 - 8^4) / (2^4 + 4^2)?
(4^8 - 8^4) / (2^4 + 4^2)
((2^2)^8 - (2^3)^4 ) / ( 2^4 + (2^2)^2 )
(2^16 - 2^12) / (2^4 + 2^4)
(2^12 (2^4 - 1)) / (2^4 (1+1))
(2^12 (15)) / (2^4 (2))
(2^12 (15)) / 2^5
2^7 * (15)
What is √5 * √45?
√5*45
√225
15
What is √3 * √27?
√3*27
√81
9
what is √5000 / √50?
√5000/50
√100
10
What is (√54 * √3) / √2 ?
√54 * 3 / √2
√168 / √2
√81
9
What is √32?
Divide up 32…..
32 = 2 * 16
√16 * √2
4 * √2
what is √180?
Divide up 180
2 * 90
3 * 60
4 * 45
5 * 36
The easiest is 5 * 36
√5 * √36
√5 * 6
What is √135?
Divide up 135
3 * 45
6 * 22.5
9 * 15
√9 * √15
3 * √15
What is √35^2 - 21^2?
Find a common ground…
35 = 5 * 7….. and 21 = 3 * 7
√7^2 (5^2 - 3^2)
√7^2 (25-9)
√7^2 (16)
√7^2 (4^2)
7 * 4
28
What is √6 * (5^6 + 5^7)?
√6* (5^6(1+5))
√6 * (5^6 (6))
√6^2 * 5^6
6 * 5^3
6 * 125
750
what is √(11^4 - 11^2)/ 30?
(11^2 (121 - 1)) / 30
(11^2 (120)) / 30
11^2 * 4
11^2 * 2^2
11 * 2
22
What is √5^7 - 5^5 + 5^4?
√5^4(5^3 - 5^1 + 5^0)
√5^4 (125 - 5 + 1)
√5^4 (121)
√5^4 (11^2)
5^2 * 11
25 * 11
275
What is the reciprocal?
The number (B) for any number (A) that makes A*B = 1.
5 = Reciprocal is ⅕ as 5*⅕ = 1
⅔ = reciprocal is 3/2 as ⅔ * 3/2 = 1
what is the reciprocal of -⅚?
The reciprocal will be the opposite so switching:
6/-5
(-5 / 6) * (6 / -5) = 1
How do you divide something by a fraction?
You simply multiply by that fraction’s reciprocal = you simply flip the numerator and denominator of that fraction.
What must you be aware of if there is addition or subtraction in the fraction’s NUMERATOR?
You MUST divide with the ENTIRE denominator. Thus, you have to find common factors and simplify.
You can split up into two fractions
What must you be aware of if there is addition or subtraction in the fraction’s DENOMINATOR?
You are NOT allowed to split up into two fractions in the same way. You ALWAYS have to divide the numerator by the ENTIRE denominator.
What is a/12 - b/6 - b/4?
First, find a common denominator
a/12 - 2b/12 - 3b/12
next, add it together:
(a - 5b) / 12
What is √3/2 - √2/3?
What is 0.0004 * 0.032?
Calculate it as… 4 * 34 = 128.
Next… count the numbers AFTER the decimal.
0.0004 * 0.032 (7 numbers)
Now move the decimal point 7 to the left from 128.00
0.0000128
What is 80 % of 75 % of 120?
8/10 * ¾ * 120
8/1 * ¾ * 12
4/1 * 3/1 * 12
4 * 3 * 12
72
What is 72.12 * 10^-4?
Move the decimal 4 times to the left.
72.12
=
0.007212
what is 12.6 / 0.3?
Multiply both the numerator and denominator by 10 to get
126 / 3
42
what is 2.10 * 0.08?
Take it as
21 * 8 = 168
Now count the numbers AFTER the decimal points.
2.1 * 0.08 (3 numbers).
Move the decimal 3 to the left.
168.00 becomes 0.168.
What is 0.49 / 0.07?
Multiply both the numerator and denominator by 100 to get
49 / 7
7
What is 1.5 / ( ⅝ - 50 %)?
1.5 / (0.125)
Rewrite to fractions:
3/2 / ⅛
Use the reciprocal rule:
3/2 * 8/1 = 24/2 = 12
What is x when 30 % less than x is 63?
0.7x = 63
7x = 630
630/7 = 90
What percentage decrease is x IF 75 - x % is 54?
75 - x/100 *75 = 54
75-54 = 75x/100
21 = 75x/100
21 = 3x/4
7 = x/4
4*7 = 28 = x
28 %.
10 % of 30 % of what number is 200 % of 6?
200 % of 6 = 12
10 % of 30 % = 3 % of x
3% of x = 12
100/3 * 12 = x
100 * 4 = x
x = 400.
If there are 24 white marbles and 36 marbles in a bag, what is the ratio of blue to white marbles?
White = 24 = 2/5
Blue = 36 = 3/5
Total = 60 = 5/5
BLUE 3 to WHITE 2
3:2
Arjun has a record of winning 3 tennis matches for every 2 he loses. If he played 30 matches, how many did he win?
Win 3 = 3:5
Lose 2 = 2:5
Total 5 = 5:5
If 30 matches, he would win ⅗ * 30 = 18 matches.
What is x and y IF -2x + y = 1 AND 2(x - 3y) = 2
2(x - 3y) = 2
becomes
2x - 6y = 2
We can now eliminate x by adding the two equations together
2x - 6y = 2
- 2x +y = 1
- 5y = 3
y = -⅗
and x can be found substituting the number for y in to any of the equations.
- 2x + -⅗ = 1
- 2x = 1 ⅗
- 2x = 8/5
- x = ⅘
x = - ⅘
If 4^y = 8^y+1, then 2^y is what?
4^y = 8^y+1
Find a common base…
(2^2)^y = (2^3)^y+1
when having a common base we can now simply set the exponents equal to each other and solve…
2y = 3(y+1)
2y = 3y + 3
y = -3
so… 2^y = 2^-3 = ⅛
If (2x + 6(9-2x)) / (x-4) = -3, what is x?
First, multiply both sides with the denominator such that…
2x + 6(9 - 2x) = -3(x-4)
2x + 54 - 12x = -3x + 12
- 7x = -42
- x = -6
x = 6
If a/c + b/3c = 1, what is “c” in terms of a and b?
a/c + b/3c = 1
First get a common denominator
3a / 3c + b/3c = 1
Now multiply the denominator to both sides
3a + b = 1*3c
3a + b = 3c
c = a + b/3
What is the value of P when c = 100 and P = 300*c^2 - c?
P = 300 * 100^2 - 100
P = 300* 10,000 - 100
P = 3,000,000 - 100
P = 2,999,900
What is ((√3x + 1) / 2) - 1 = 3. what is x?
multiply by 2 to remove the denominator.
√3x + 1 -2 = 6
√3x + 1 = 8
square both sides
3x + 1 = 64
3x = 63
x = 21
What is x if 13 / (x + 13) = 1
13/(x + 13) = 1
13 = 1(x + 13)
13 = x + 13
x = 0
2h - 4k = 0 and
k = h -3
2h - 4(h - 3) = 0
2h - 4h + 12 = 0
12 = 2h
h = 6
k = h - 3
k = 6 - 3 = 6
What is b and g if…12b = 2g and 4g - 3b = 63?
12b = 2g
6b = g
4g - 3b = 63
substitute g with 6b…
4*6b -3b = 63
24b - 3b = 63
21b = 63
b = 3
then g will be…
6b = g
g = 6*3 = 18.
If y - 2x - 1 = 0
and… x -3y - 1 = 0
what is the values of x and y?
First, rewrite the two equations for them to be as similar as possible…
y - 2x = 1
-3y + x = 1
now multiply the second equation with 2 to get an equal value of x for the two equations.
2(-3y + x) = 1*2
-6y + 2x = 2
Now add the two equations to eliminate x.
y - 2x = 1
- 6y + 2x = 2
- 5y = 3
y = - ⅗
2x = 1 + y
2x = 1 + 3/5
2x = 8/5
x = 4/5
If 2p = (m - 5) / (n +2), what is m in terms of n and p?
We need to isolate m…
2p (n+2) = m - 5
2pn + 4p + 5 = m
What is the value of z if… 2^x+y = √(z - 2) and… x = 2 - y
2^x+y can be re-written as we know that x = 2 - y
2^(2-y)+y
so…
2^(2-y)+y = √(z - 2)
2^2 = √(z - 2)
Now we square both sides…
(2^2)^2 = z - 2
16 = z - 2
z = 18.
Rewrite x^2 + 14x + 33
To rewrite, we want it in the form…
(x ….)(x….).
to figure out what should be in the parentheses besides x, we have to look at the number “33” and figure out its factors AND find a set of factors that can yield 14 as well.
The factors of 33 are: 1 and 33. 3 and 11.
1 and 33 can never become 14.
3 and 11 can be added to become 14 so that is the set of factors we want.
(x + 3) (x + 11) = x^2 + 14x + 33
what is x IF x^2 - 15x = - 26?
first, recognize that there most likely will be two different solutions as we have x^2.
x^2 - 15x = -26
x^2 -15x + 26 = 0
(x - 2) (x - 13) = 0
x - 2 = 0, then x = 2
x - 13 = 0, then x = 13.
X is either 2 or 13.
What is x IF x^3 - 2x^2 = 3x?
First recognize that we might have three different solutions as x^3.
Now factor out x.
x^3 - 2x^2 = 3x
x^3 - 2x^2 - 3x
x (x^2 - 2x - 3)
x ( (x - 3) (x + 1)) = 0
x = 0, then x = 0
x - 3 = 0, then x = 3
x + 1 = 0, then x = -1
What is ( x^2 + 7x + 12) / (x + 3) = ?
Rewrite the numerator
x^2 + 7x + 12
((x + 3) (x + 4)) / (x + 3)
We can remove (x + 3) from both numerator and denominator
We get…
(x + 4)
what is y IF …. y^2 - 11y + 30 = 0?
y^2 - 11y + 30 = 0
(y - 5) (y -6) = 0
y - 5 = 0, then y = 5
y - 6 = 0, then y = 6
what is x IF…. x^3 - 5x^2 + 4x = 0?
x^3 - 5x^2 + 4x = 0
x (x^2 - 5x + 4) = 0
x ( (x - 1)(x - 4) ) = 0
x = 0, then x = 0
x - 1 = 0, then x = 1
x- 4 = 0, then x = 4
what can you reduce the following expression to? (a^2 - b^2) / (a - b)
(a^2 - b^2) / (a - b)
Write out the numerator…
((a + b) ( a - b)) / ( a- b)
Reduce…
(a + b).
What can you reduce the following expression to? (2t - 1 + (2t-1)^2 ) / (2t - 1)
(2t - 1 + (2t-1)^2 ) / (2t - 1)
write out the numerator
(2t - 1 + ((2t-1)(2t-1))) / (2t - 1)
now factor out (2t - 1)…
(2t-1) (1 + (2t - 1)) / (2t-1)
Reduce…
(1 + (2t - 1))
1 + 2t - 1
2t…
What can you reduce the following expression to? …. (3x^2 - 6x - 45) / (3x + 9)
(3x^2 - 6x - 45) / (3x + 9)
factor the numerator / rewrite…
((3x + 9)(x - 5)) / (3x+9)
Reduce…
(x - 5)
What can you reduce the following expression to? (5ab + abc) / (abc^2 + 10abc + 25ab) ?
(5ab + abc) / (abc^2 + 10abc + 25ab) ?
First factor out “ab”.
(ab (5 + c)) / (ab (c^2 + 10c + 25))
reduce…
(5 + c) / (c^2 + 10c + 25)
rewrite the denominator…
(5 + c) / ((c + 5)(c + 5))
Reduce…
1 / (5 + c)…
What is the solution to |−x - 4| > 8 ?
|−x - 4| > 8
- x -4 > 8 -(-x) - (-4) > 8
- x > 12 x + 4 > 8
x < -12 x > 4
what is the solution to 2(x-1)^3 + 3 < 19 ??
2(x-1)^3 + 3 < 19
2(x-1)^3 < 16
(x-1)^3 < 8
x-1 < 2
what is the solution to…. 2 |x + 0.32| = 7
2 |x + 0.32| = 7
x + 0.32 = 3.5
x + 0.32 = 3.5 -x - 0.32 = 3.5
x = 3.18 -x = 3.82
x = -3.82
What is the solution to…. |x/4 + 3| = 0.5
x/4 + 3 = 0.5 -x/4 - 3 = 0.5
x/4 = -2.5 -x/4 = 3.5
x = -10 -x = 14
x = -14
What is the solution to…. |x^3| < 64
x^3 < 64 -x^3 < 64
x < 4 -x < 4
x > -4
A hose is placed into an empty pool and turned on at 2:00 pm. the pool, which holds 680 gallons of water, reaches its capacity at 5:24 pm. How many gallons of water per hour did the hose add to the pool?
680 gallons
Time: 5:24pm - 2:00pm = 3 hours and 24 minutes.
680g / 3:24h
680g / 204m = 3 ⅓
3 ⅓g/m * 60 = 200 gallons of water per hour
40 students in a class of 200 got A’s on their test. 64 got B’s, 18 got D’s and 6 got F’s. If students can only get A, B, C, D or F as grades, what percent of the students got C’s?
a = 40
b = 64
c = ?
d = 18
e = 6
t = 200
40 + 64 + 18 + 6 + c = 200
c = 72
72 / 200 = 36 %.
The temperature in Limerick is ¾ that in Cairo, where the temperature is 8/5 that in Halifax. If the temperature in Limerick is 66 degrees, what is the temperature in Halifax?
L = 66
L = ¾ C
C = 8/5 H
H = ?
L = ¾ (8/5H)
L = 24/20H
L = 6/5H
66 = 6/5H
66* ⅚ = H
H = 55
At a convention of monsters, ⅖ have no horns, 1/7 have one horn, ⅓ have two horns, and the remaining 26 have three or more horns. How many monsters are attending the convention?
⅖ no horns
1/7 one horn
⅓ two horns
26 three or more horns
⅖ + 1/7 + ⅓
35/105 + 15/105 + 35/105 = 92/105
105/105 - 92/105 = 13/105
13/105*m = 26
m = 26 * 105/13
13m = 26*105
13m = 2730
m = 210
Of all the homes on Gotham Street, ⅓ are termite-ridden, and ⅗ of these are collapsing. What fraction of the homes are termite-ridden, but NOT collapsing?
Ft = ⅓
Ft+c = ⅓ * 3/5 = 3/15
Ft-c = Ft - Ft+c
Ft-c = ⅓ - 3/15
Ft-c = 5/15 - 3/15 = 2/15
A plane leaves Chicago in the morning and makes three flights before returning.The first flight has traveled twice as far as the second flight, and the second flight traveled three times as far as the third flight. If the third flight was 45 miles, how many miles was the first flight?
F1 = 2*F2
F2 = 3*F3
F3 = 45
F1 = ?
F1 = 2(3*F3)
F1 = 6*F3
F1 = 6*45
F1 = 270 miles.
Arnaldo earns $11 for each ticket that he sells, and a bonus of $2 per ticket for each ticket he sells over 100. If Arnaldo was paid $2,400, how many tickets did he sell?
Q2 * P + Q2(P+2) = 2400
100*11 + Q2(11+2) = 2400
1100 + Q2(13) = 2400
Q2*13 = 1300
Q2 = 1300
Q = Q1 + Q2
Q = 100 + 100 = 200.
Amar is 30 years younger than Lauri. In 5 years, Lauri will be three times as old as Amar. How old will Lauri be in 10 years?
A = L - 30, L = A + 30
L in + 10y?
L + 5 = 3A
L+5 = 3(L - 30 +5)
L+5 = 3L - 75
80 = 2L
40 = L
L + 10 = ?
40 + 10 = 50.
What is the temperature in Fahrenheit when it is 30 degrees Celsius? C = 5/9(F - 32)
C = 30
C = 5/9(F - 32)
30 = 5/9(F-32)
270 = 5F - 160
430 = 5F
86 = F
Joe’s car can travel 36 miles per gallon of fuel. Approximately how many kilometers can the car travel on 10 liters of fuel? (5 miles = approximately 8 kilometer; 1 gallon = approximately 4 liters).
36m / g * 8km /5m = 288km / 5gallons
288km/5gallons * 1gallon/4liters
288km / 20liters
- 4 kilometers/l
- 4 km/l * 10 liters = 144 kilometers.
Svetlana is running a 10-kilometer race. She runs the first 5 kilometers of the race at a speed of 12 kilometers per hour. At what speed will she have to fun the last 5 kilometers of the race if she wants to complete the 10 kilometers in 55 minutes?
Distance = Rate * Time
5 = 12 * t
5 = 12t
t = 5/12
55 minutes * 1hour/60minutes = 55/60 = 11/12
11/12 - 5/12 = 6/12 = 1/2
The last 5 kilometers will be….
Distance = Rate * Time
5 = r * 0.5
r = 10 km/t.
What is arc length?
A section of circle’s circumference.
what is central angle?
The angle created by any two radii..
Fx. the angle determining what big a share a sector is of a whole circle
What is sector area?
A “wedge” of the circle, composed of two radii and the arc connecting these two radii.
What is the hypotenuse?
The longest side of a RIGHT triangle. The hypotenuse is opposite the right angle.
What are the 5 pythagorean triplets?
8-15-17
5-12-13 and double up: 10-24-26
3-4-5 and double up: 6-8-10
True or false? The point (4,14) is on the curve y = x^2 - 2.
The equation y = 3x + 4 is already in y = mx + b form.
For the point 4, 14. to be on the curve, you can plug in x = 4 into the equation.
y = 4^2 - 2
y = 16 -2
y = 14.
Which is the y-coordinate we were given so the answer is YES.
A sector has a central angle of 270 degrees. If the sector has a radius of 4, what is the area of the sector?
270/360 = ¾ of a circle.
The circles Radius is 4.
So TOTALarea = 4^2*π = 16π
16π * ¾ = 12π.
A sector has a radius of 8 and an area of 8π. What is the arc length of the sector?
SectorRadius = 8
SectorArea = 8π
TOTALarea = 8^2*π = 64π
8π / 64π = ⅛.
TOTALcircumference = D*π = (2*8)*π = 16π
SECTORarclength = 16π * ⅛ = 2π
A sector has an arc length of π/2 and a central angle of 45 degrees. What is the radius of the sector?
SECTORarclength = π/2
SECTORcentralangle = 45
SECTORradius?
45/360 = ⅛. = the sector is ⅛ of the circle
So… π/2 is ⅛ of the circumference of the circle.
8π / 2 = 4π = TOTALcircumference
C = D * π
C = (2*r)*π
So the squareroot(4)*π = 2π.
SECTORradius = 2.
Two sides of a triangle have lengths 4 and 8. Which of the following are possible side lengths of the third? a = 2, b = 4, c = 6, d = 8
8+4 = 12
8-4 = 4
4 < x < 12
only c = 6 and d = 8 works.
diameter of the circle = 9.
Area of circle = r^2 * π
Area of circle = 4.5^2 * π = 20.25π
A = 49
A = S*S
S = squareroot(49) = 7.
A^2 + B^2 = C^2
7^2 + 7^2 = 98
squareroot of 98 = C
98 can be broken down… square root of 98 = squarerootof( 2*7*7) = 7*squareroot(2)
Does the point (3, -2) lie on the line y = 2x - 8?
Plug in x = 3 and see if it results in y = -2.
y = 2*3 - 8 = -2.
YES…
For the line y = 4x +2, what is the y-coordinate when x = 3?
Plug in x = 3 and see…
y = 4*3 + 2 = 14.
In the coordinate plane, a circle has center (2, -3) and passes through the point (5, 0). What is the area of the circle?
A = r^2 * π
A = (2 - 5)^2 + (-3 + 0)^2 * π = (9 + 9)π = 18π
What is (0.0036*2.8) / ( (0.04)*(0.1)*(0.003))?
(0.0036*2.8) / ( (0.04)*(0.1)*(0.003))
(36*10^-4) * (28*10^-1) / ( (4*10^-2)*(1*10^-1)*(3*10^-3))
(36*28 / 4*1*3) * 10^(-4-1)-(-2-1-3)
36/3 * 28/4 * 10^-5-(-6)
12*7*10^1 = 840.
What is a quotient and a remainder?
When x and y are positive integers, there exist unique integers q and r, called the quotient and remainder:
y = x*quotient + remainder, and 0 < r < x
What is the quotient and remainder of y =29 when x =3?
y = x*quotient + remainder
29 = 9*3 + 2
Is 0 positive or negative?
It is NEITHER positive or negative. It is just 0.
Are 8/36 and 14/63 equivalent?
Yes…
they are EQUIVALENT as both represent 2/9
What are mixed numbers?
Numbers that consist of both a whole number and a fraction.
fx… 7⅔
7⅔ = 23/3
What is I x + y I equal to?
I x + y I < I x I + I y I
as… if x = 10, y = 2
10+2 = 10 +2 = 12 < 12
and…
if x = 10 and y = -2
then…
10 - 2 = 10 + 2 = 8 < 12
What is the formula for calculating the PERCENTAGE increase/decrease?
Take…
(New number - Original number) / Original number
(30 - 24) / 24 = 6 / 24 = 0.25 = 25 %
What is 0!, 1!, 2! and 3!?
0! = 1 (by definition 0! = 1)
1! = 1
2! = 1*2 = 2
3! = 1*2*3 = 6
What are the permutations of A, B and C?
Essentially how many ways can you order A, B and C?
The answer is “3!”
3(n-1)(n-2) = 3*2*1 = 6
If you have the letters, A, B, C, D and E…, how many combinations can you make when only choosing 2 items at a time?
n = 5
k = 2
5! / (2! (5-2)!)
5! / (2! * 3!)
120 / 2*6
120 / 12
10 combinations
What is P(a) = 0.3 + P(b) = 0.42 IF 1) P(a) and P(b) are mutually exclusive? and 2) if P(a) and P(b) are independent?
P(a or b) = P(a) + P(b) (where A and B are mutually exclusive)
0.3 + 0.42 = 0.72 = 72 %
P(a or b) = P(a) + P(b) - P(a)*P(b) (where A and B are independent events)
0.3 + 0.4 - 0.3*0.42 = 0.7 - 0.126 = 0.574 = 57.4 %
What are the solutions to x(x-3)(x^2+5) / x-4?
A fraction equals 0 if and only if its numerator equals 0.
Thus… x(x-3)(x^2+5) = 0
x=0, x-3=0 or x^2+5=0
x=0 or x=3 but there is no solution to x^2+5=0 as x^2 + 5 > 0 for all real numbers.
Thus, the two only solutions are x=0 and x=3.
what is the formula used to find the roots of quadratic expressions and when is it relevant?
When you cannot factor a quadratic expression, you can always find its roots with the following formula..
What is the rules regarding lengths of 45-45-90 degrees triangles and 30-60-90 triangles?
If n = 33^43 + 43^33, what is the units digit of n?
Both numbers are raised to 3.. 33 and 43 so they will follow the sequence of 3,9,7,1,3,9,7,1… as 3^1 = 3, 3^2 = 9, 3^3 = 27 and 3^4 = 81.
thus…. the 43rd number will be 7 and the 33rd number will be 3.
7+3 = 10 = 0
If x is a positive integer greater than 1, what is the value of x ?
2x is a common factor of 18 and 24.
x is a factor of 6.
The answer is A.
X > 1, then 2*x = > 4 AND has to be a common factor of 18 and 24.
The factors of 18 are… 1,2,3,6,9,18 and the factors of 24 are 1,2,3,4,6,8,12,24
The only common factor that is >4 is 6.
2x = 6 and then x = 3
2) X is a factor 3 AND greater than 1. It can be either 2, 3 or 6.
If a triangle is circumscribed by a circle such that one of its sides is a diameter of the circle, what can be said about that triangle?
That it will be a right triangle.
How do you calculate the slope of a line using two coordinates?
On a 400-mile trip, Car X traveled half the distance at 40 miles per hour and the other half at 50 mph. What was the average speed of car x?
- First determine the total traveling time
200 miles / 40 miles per hours = 5 hours
+
200 miles / 50 miles per hour = 4 hours
=
9 hours total
400 miles / 9 hours = 44 4/9 miles per hour.
If machine X can produce 1,000 bolts in 4 hours and Machine Y can produce 1,000 bolts in 5 hours, in how many hours can Machines X and Y, working together at these constant rates, produce 1,000 bolts?
1/r + 1/s = 1/h
1/machine x + 1/machine y = 1/combined time
¼ + ⅕ = 1/h
5/20 + 4/20 = 1/h
9/20 = 1/h
9h = 20
h = 20/9
h = 2 2/9
Working together, Machines X and Y can produce 1,000 bolts in 2 hours and 2/9 hours.
How many liter of a solution that is 15 % salt must be added to 5 liters of a solution that is 8 % salt so that the resulting solution is 10 % salt?
0.15n + 0.08(5) = 0.10(n+5) (multiply both sides by 10)
15n + 40 = 10n + 50
5n = 10
n = 2
So add 2 liters and we get a total of 5+2= 7 liters, which now has a salt percentage of 10.
The price of an item is discounted by 20 % and then this reduced price is further discounted by an additional 30 %. These two discounts are equal to an overall discount of what percentage?
The discounted price is…
0.8p
After second discount…
0.7*0.8p = 0.56p.
1-0.56 = 0.44 = 44 % total discount.
Each of 25 people is enrolled in history, mathematics or both. If 20 are enrolled in history and 18 are enrolled in mathematics, how many are enrolled in both history and mathematics?
History = 20-n
Both = n
Mathematics = 18-n
(20 - n) + n + (18 - n) = 25
38 - n = 25
-n = -13
n = 13
In a certain production lot, 40 % of the toys are red and the remaining toys are green. Half of the toys are small and half are large. If 10 % of the toys are red and small, and 40 toys are green and large, how many of the toys are red and large?
If p is the product of the integers from 1 to 30, inclusive, what is the greatest integer k for which 3k is a factor of p ?
During a trip, Francine traveled x percent of the total distance at an average speed of 40 miles per hour and the rest of the distance at an average speed of 60 miles per hour. In terms of x, what was Francine’s average speed for the entire trip?
A worker carries jugs of liquid soap from a production line to a packing area, carrying 4 jugs per trip. If the jugs are packed into cartons that hold 7 jugs each, how many jugs are needed to fill the last partially filled carton after the worker has made 17 trips?
Carrying 4 jugs per trip, the worker carries a total of 4(17) = 68 jugs in 17 trips. At 7 jugs per carton, these jugs will completely fill 9 cartons with 5 jugs left over since (9)(7) + 5 = 68. To fill the 10th carton, 7 – 5 = 2 jugs are needed.
How many prime numbers between 1 and 100 are factors of 7,150 ?
To find the number of prime numbers between 1 and 100 that are factors of 7,150, find the prime factorization of 7,150 using a method similar to the following:
7,150=10×715=(2×5)×(5×143)=2×5×5×(11×13)7,150=10×715=(2×5)×(5×143)=2×5×5×(11×13)
Thus, 7,150 has four prime factors: 2, 5, 11, and 13.
Team A and Team B are competing against each other in a game of tug-of-war. Team A, consisting of 3 males and 3 females, decides to line up male, female, male, female, male, female. The lineup that Team A chooses will be one of how many different possible lineups?
Any of the 3 males can be first in the line, and any of the 3 females can be second. Either of the 2 remaining males can be next, followed by either of the 2 remaining females. The last 2 places in the line are filled with the only male left followed by the only female left. By the multiplication principle, there are 3 × 3 × 2 × 2 × 1 × 1 = 36 different lineups possible.
In an electric circuit, two resistors with resistances x and y are connected in parallel. In this case, if r is the combined resistance of these two resistors, then the reciprocal of r is equal to the sum of the reciprocals of x and y. What is r in terms of x and y ?
In Country C, the unemployment rate among construction workers dropped from 16 percent on September 1, 1992, to 9 percent on September 1, 1996. If the number of construction workers was 20 percent greater on September 1, 1996, than on September 1, 1992, what was the approximate percent change in the number of unemployed construction workers over this period?
If n = 38 − 28, which of the following is NOT a factor of n ?
- 97
- 65
- 35
- 13
- 5
Car 1 starts from point A and heads for point B at 60 mph. Fifteen minutes later, car 2 leaves the same point A and head for point B at 75 mph. How long before car 2 overtakes car 1?
Two planes leave the same point at 8 am. Plane 1 heads EAST at 600 mph and Plane 2 heads West at 450 mph. How long will they be 1400 miles apart? and how long did each plane travel?
Two planes leave the same point at 8 am. Plane 1 heads EAST at 300 mph and Plane 2 heads West at 550 mph. How long will they be 3200 miles apart?
Car 1 starts from point A and heads for point B at 40 mph. Twenty minutes earlier, car 2 left the same point A and headed for point B at 30 mph. How long before car 1 overtakes car 2?
A boat can go 10 miles upstream in 30 minutes. The return trip downstream takes only 20 minutes. what is the speed of the boat in still water and the speed of the current in mph?
What is “ - l -13 -(-17)l?
It will be…. - l-13 +17l
which is… - l-4l
What is the sum of x, y, and z when… x+y=8, x+z=11 and y+z=7?
Write it up…
x + y = 8
x + z = 11
y + z = 7
2x + 2y + 2z = 26
so….
x + y + z = 13
What are the solutions to…. 22 - ly+14l = 20?
22 - l y + 14 l = 20
that is… - ly + 14l = -2
which is.. l y + 14l = 2
and…
y + 14 = -2 or…. y + 14 = 2
y = - 16 or… y = - 12
Plug in to check…
l-16 + 14l = 2 AND l-12 + 14l = 2
Ok.
What is the solutions to a, b and c when….
a + b = 10
b + c = 12
a + c = 16
We know that…
2a + 2b + 2c = 38
so…
a + b + c = 19
then…
19 - 10 = 9 = c
19 - 12 = 7 = a
19 - 16 = 3 = b
If x = 4^20 + 4^21 + 4^22, what is the largest prime factor of x?
First factor out the common factor…
x = 4^20(1+4^1 + 4^2)
x = 4^20(1+4+16)
x = 4^20(21)
x = 4^20(3*7)
so the biggest prime factor is 7.
What is (4/9)^(-3/2) ?
(4/9)^(-3/2)
remove the negative sign in the exponent by flipping
(9/4)^3/2
Take the square root of numerator and denominator and then exponent 3
3^3/2^3 = 27 / 8
What is (4^y+4^y+4^y+4^y)(3^y+3^y+3^y)?
Factor…
4^y(1+1+1+1)*3^y(1+1+1)
4^y(4)*3^y(3)
4^y+1 * 3^y+1
(4*3)^y+1
12^y+1
If m and n are positive integers, what is m when… (2^18)(5^m) = (20^n)?
2^18 * 5^m = (2*2*5)^n
2^18 * 5^m = 2^2n * 5^n
now just set the exponents equal to each other…
18 = 2n and… m = n
n = 9 = m = n
What is the difference between x^2 = 16 and x = squareroot of 16?
x^2 = 16 has two solutions: -4 and 4.
Squareroot(16) only has one solution = 4. the positive solution.
What is √63 + √28?
They can translate into…
√9*7 + √4*7
3*√7 + 2*√7
5*√7
What is √150 - √96?
They must be rewritten….
√6 * 25 - √6 * 16
5*√6 - 4√6
1*√6
√6
What is D when… d/4 + 8/d + 3 = 0?
First…
d + 4*8 / d = -3*4
d^2 + 32 = -12d
d^2 + 12d - 32 = 0
(d + 8) (d - 4) = 0
d = -8
d = 4
Given that (p-3)^2 - 5 = 0, what is p?
(p - 3)^2 - 5 = 0
(p-3)^2 = 5
√(p-3)^2 = √5
l p-3 l = √5
p = 3 +/- √5
What is… (3 - √7)(3 + √7)?
9 - 3*√7 + 3*√7 - 7 = 2
Hugo lies on top of a building, throwing pennies straight down to the street below. The formula for the height, H, that a penny falls is H = V*t+ 5*t^2, where V is the original velocity of the penny (how fast Hugo throws it when it leaves his hand) and t is equal to the time it takes to hit the ground. The building is 60 meters high, and Hugo throws the penny down at an initial speed of 20 meters per second. How long does it take for the penny to hit the ground?
H = V*t + 5*t^2
60 = 20t + 5*t^2
5*t^2 + 20*t - 60 = 0
5(t^2 + 4t - 12) = 0
5/t+6)(t-2) = 0
t = -6 or t = 2.
T must be positive so t = 2
What is z when z^2 - 10z + 25 = 9?
z^2 - 10z + 25 = 9
(z+5)^2 = 9
√(z+5)^2 = √9
z+5 = 3
z = 5 +/- 3
If.. w ? F = (√F)^w, what is 4 ? (3 ? 16)?
First take the parantheses…
(3 ? 16) = (√16)^3 = 4^3 = 64
now… 4 ? 64
(√64)^4 = 8^4 = 4,096
By which factor does t*b^4 increase, when we double b?
t*b^4 vs t*2b^4
tb^4
tb^4 = t*(2b(^4) = t(2b*2b*2b*2b) = t*16b^4 = 16tb^4
16 times bigger.
If Sn = 15n - 7, what is S7 - S5?
S7 = 15*7 - 7 = 14*7 = 98
S5 = 15*5 - 7 = 75 - 7 = 68
98-68 = 30
An = 2*An-1 - 4 and A6 = -4, what is A4?
We know A6 and the formula for calculating An so we plug in and first find A5 and then A4 working our way backwards…
A6 = 2*A5 - 4
-4 = 2*A5
0 = 2*A5
A5 = 0
Knowing that A5 = 0, we can find A4….
A5 = 2*A4 - 4
0 = 2*A4 - 4
4 = 2*A4
2 = A4
If Sn = 3^n, what is the units digit of S65?
3, 9, 27, 81
Digit 65 will be a 3.
If A @ B = 4A - B, what is (3 @ 2) @ 3?
Take the parentheses first…
(3 @ 2) = 4*3 - 2 = 10
Now…
10 @ 3 = 4*10 - 3 = 40 - 3 = 37
If A€B = A^2 + B^2 + 2AB, what is a+b if A€B = 9?
We know that…
A^2 + B^2 + 2AB = 9
(A+B)(A+B) = 9 or… (-A-B)(-A-B) = 9
(A+B)^2 or (-A - B)^2
so… A+B = 3 or -3
Life expectancy is defined by the formula (2SB)/G, where S=shoe size, B = avg. electric bill and G=GMAT score. If Melvin’s GMAT score is twice his electric bill, and his life expectancy is 50, what is his shoe size?
L = (2SB)/G
and we know that L=50 and that 2*B = G
so…
50 = (2*S*B) / (2*B)
50 = S
Shoe size = 50.
The competitive edge of a baseball team is defined by the formula √(W/L), where w = #of wins and L = # of losses. This year, the GMAT all-stars had 3 times as many wins as last year and one-half as many losses as they had last year. By what factor did their competitive edge increase?
√(W/L) = √(1) last year
√(3W/0.5L) = √(6) this year
So essentially it increased by √6
If An = 3 - 8n, what is A1?
Simple…
A1 = 3 - 8*1 = -5
If An = 3 - 8n, what is A11-A9?
An = 3 - 8n.
then…
A11 = 3 - 8*11 = -85
A9 = 3 - 8*9 = -69
Difference is -16.
If An = (An-1 * An-2) / 2, and A5 = -6, and A6 = -18, what is A3?
We can work our way backwards from the information given…
First, we find A4…
- 18 = (-6 * A4) / 2
- 36 = -6 * A4
A4 = -36 / -6 = 6
knowing A4, we can find A3….
A5 = (A4 * A3) / 2
- 6 = (6 * A3) / 2
- 12 = 6 * A3
A3 = -12 / 6 = -2
If Sn = (4^n) + 3, what is the units digit of S100?
First we have to know the pattern for the roots of 4…
4^1 = 4
4^2 = 16
4^3 = 64
4^4 = 256
4^100 will have a units digit of 6.
So we just have to add 3.
6+3 = 9.
The first term in an arithmetic sequence is -5 and the second term is -3, what is the 50th term?
We know that the change is +2.
we have the first two.. so 50-2 = 48..
48*2 = 96.
-3 + 96 = 93 will be the 50th term.
If 1 > 1 - A*B > 0, which of the following must be true?
A/B > 0
A/B < 1
A*B < 1
First rewrite…
1 > 1 - A*B > 0 (subtract 1 from all)
0 > -A*B > -1 (multiple by -1)
0 < A*B < 1
so… A*B is between 0 and 1. thus they must both be positive and
A/B > 0 = true
A/B < 1, may be true but we dont know if a or b is biggest
A*B < 1 is true
Is m*n < 10?
- m < 2
- n < 5
Each of the two information pieces is insufficient.
together they are still insufficient as it could be two negative numbers such as -2*-6 = 12.
What is the solution to… l x+2 l < 5 ?
-5 < x < 5
“+2” by “-2 on both”
-7 < x < 3
Now -2 is the centerpoint.
Alternatively look at it this way..
x+2 < 5
x < 3
- x-2 < 5
- x < 7
x > -7
What is the solutions to… l x-4 l < 3
-3 < x < 3
“-4” by adding 4 to both
1 < x < 7
4 is now the centerpoint.
alternatively..
x-4 < 3
x < 7
- x -(-4) < 3
- x < -1
x > 1
what is the simplified version of… -3x + 7 < 2x + 32
- 3x + 7 < 2x + 32
- 25 < 5x
- 5 < x
What can be said about G, if G^2 < G?
then G has to be:
0 < G < 1
If 4x - 12 > x + 9 which of the following must be true?
- x>6
- x<7
- x>7
- x>8
- x<8
4x - 12 > x + 9
3x > 21
x > 7
So …. x>6 is the only option for sure.
If 0 < ab < ac, is a negative?
- c < 0
- b > c
A must be negative for negative C*A to be positive. 1 is sufficient.
if b > c, and a*b < a*c, then b must be a negative number that is less negative than c and a must be negative for both to turn positive numbers for the multiplications.
D is the answer. Each is sufficient.
What should you immediately imply from x*y > 0
X and y are both positive OR both negative
What should you immediately imply from x*y < 0
x and y have different signs
What should you immediately imply from x^2 - x < 0
x^2 < x so… 0 < x < 1
Is…. (-¾)^3 > -¾ ?
The answer is yes as ¾ < 1 and thus becomes closer to 0 when taken to any root.
What can be said if… B^3 * A < 0 and A > 0?
We know that B must be a negative number as B^3 must be negative and anything raised to an uneven power will keep its sign.
What is a when (b+a)/2a = 2, and a+b = 8.
Plug in a+b = 8.
8/2a = 2
8 = 4a
a = 2
Eco wildlife preserve contains 5x zebras and 2x lions, where x is a positive integer. If the lions succeed in killing z of the zebras, is the new ratio of zebras to lions less than 2:1?
- z > x
- z = 4
What we are asked is….
(5x - z) / 2x < 2/1 ?
5x - z < 2*2x
5x - z < 4x
-z < -x
z > x is really what is asked.
- z > x answers this and is sufficient
- z = 4, we do not know x and cannot answer.
the answer is A.
A retailer sells only radio and clocks. If she currently has 44 total items in inventory, how many of them are radios?
- The retailer has more than 28 radios in inventory
- the retailer has less than twice as many radios as clocks in inventory
- tells us that R > 28 but is not sufficient on its own
- tells us that C+R = 44 and… 1.5R = 44 so… 3R = 88 and R = <29,3333. Not sufficient.
Together we know that 28 < R < 29.333 so R must be 29.
If x and y are nonnegative integers and x + y = 25, what is x?
- 20x + 10y < 300
- 20x + 10y > 280
So essentially just make x+y=25 to 10x+10y=250
Now use the information pieces
- 20x + 10y < 300 - 10x + 10y = 250 = 10x < 50, so x < 5
- 20x + 10y > 280 - 10x + 10y = 280 = 10x > 30, so x >3
together we can say that 3 < x < 5 s and x is an integer so it must be 4.
If a/b = 16 and a/b^2 = 8, what is a*b?
start by simply dividing the first equation by the second, you will see that b =2
(a/b) / (a/b^2) = 16/8
(a/b) * (b^2/a) = (a*b^2)/(ab) = b = 16/8 = 2
So a/2 = 16, then a = 32.
and a*b = 32*2 = 64.
What is x when… x^2 + 8x + 13 = 0?
The problem here is that there are no two integers for which the sum is 8 and the product is 13 so we cannot factor it.
Instead we must use the quadrateic formula..
x = (-8 +/- √(8^2 - 4*1*13)) / 2*1
x = (-8 +/- √(64 -52)) / (2)
x = 4 +/- (√12)/2
x = (-4 +√3, -4 - √3)
What does the discriminant in the quadratic formula tell us?
The discriminant in the quadratic formula is…
√(b^2 - 4*a*c)
- If √(b^2 - 4*a*c) > 0, there will be two solutions
- If √(b^2 - 4*a*c) = 0, there will be one solution
- If √(b^2 - 4*a*c) < 0, there will be no solution
Which of the following has no solution for x?
- x^2 - 8x - 11 = 0
- x^2 + 8x + 11 = 0
- x^2 + 7x + 11 = 0
- x^2 -6x + 11 = 0
- x^2 - 6x - 11 = 0
Here we must determine this from the discriminant from the quadratic formula, namely
√(b^2 - 4*a*c)
- x^2 - 8x - 11 = 0 …… √(-8^2 - 4*1*-11) = √64-(-44) = √108 > 0 = two solutions
- x^2 + 8x + 11 = 0… √(8^2 - 4*1*11) = √64-44 = √20 > 0 = two solutions
- x^2 + 7x + 11 = 0 … √(7^2 - 4*1*11) = √49-44 = √5 > 0 = two solutions
- x^2 -6x + 11 = 0…… √(-6^2 - 4*1*11) = √36-44 = √-8 < 0 = no solution
- x^2 - 6x - 11 = 0 …… √(-6^2 - 4*1*-11) = √36-(-44) = √80 > 0 = two solutions
What is 4 / (3-√2)?
When the denominator has a normal number AND a square root, you must use the conjugate…
for a + √b, the conjugate is given by a-√b
for a - √b, the conjugate is given by a+√b
(so the opposite sign)
thus…
4 / (3-√2) =
4*(3+√2) / (3-√2)(3+√2) =
(12 + 4√2) / (9+3*√2 - 3√2 - 2) =
(12 + 4*√2) / (7)
If a*b = 12 and c/a +10 = 15, what is b*c?
a*b = 12 is also b = 12/a
c/a + 10 = 15 is also c + 10a = 15a which is c = 5a.
So… b*c is
12/a * 5a which is 60a/a = 60.
If l x+1 l = l 3x -2 l, what can x be?
So we have two absolute value expressions…
Can be…
POS-NEG
POS-POS
NEG-NEG
NEG-POS
so either two different signs or both have the same sign. We have to calculate two options. One with same sign and one with different sign.
Lets start with different sign…
x+1 = -3x -(-2)
4x = 1
x = ¼
now both signs positive
x+1 = 3x -2
3 = 2x
x = 3/2
What is the closest integer to x*y*z when we know that… x*y=2, x*z=8 and y*z=5?
We can multiply the 3 expressions together and we get…
x^2*y^2*z^2 = 2*5*8
x^2*y^2*z^2 = 80
squareroot(x^2*y^2*z^2) = squareroot(80)
x*y*z = close to 9.
Which of the following has no solution for a?
- a^2 -6a + 7 = 0
- a^2 + 4a + 3 = 0
- a^2 - 4a + 5 = 0
We must use part of the quadratic root formula…
√(b^2 - (4*a*c))
- a^2 -6a + 7 = 0 …. √(-6^2 - (4*1*7)) = √36 - 28 = √8 > 0 (two solutions)
- a^2 + 4a + 3 = 0…. √(4^2 - (4*1*3)) = √16 - 12 = √4 > 0 (two solutions)
- a^2 - 4a + 5 = 0….. √(-4^2 - (4*1*5)) = √16 - 20 = √-4 < 0 (NO solutions)
If f(x) = 2x^4 - x^2, what is the value of f(2√3)?
f(2√3) = 2(2√3)^4 - (2√3)^2
2*16*√81 - 4√9
32*9 - 4*3
270 + 18 - 12 = 276
If g(x) = 3x + √x, what is the value of g(d^2 + 6d + 9)
g(d^2 + 6d + 9) = 3(d^2 + 6d + 9) + √(d^2 + 6d + 9)
3d^2 + 18d + 27 + √(d+3)^2
3d^2 + 18d + 27 + d + 3
3d^2 + 19d + 30
If k(x) = 4x^3*a, and k(3) = 27, what is k(2)?
We have to use the information we know about k(3).
k(3) = 4*3^3*a = 27
4*a = 27/27
4*a = 1
a = 1/4
k(2) = 4*2^3*¼ = 2^3 = 8
If f(x) = 2x^2 - 4 and g(x) = 2x, for what values of x will f(x) = g(x)?
Set the two equations equal to each other and solve…
2x^2 - 4 = 2x
2x^2 - 2x -4 = 0
2(x+1)(x-2) = 0
x = 2 or x = -1
The velocity of a falling object in a vacuum is directly proportional to the amount of time the object has been falling. If after 5 seconds an object is falling at a speed of 90 miles per hour, how fast will it be falling after 12 seconds?
So first we take 90m/h and divide by 5 to get S.
90m/h / 5 = 18m/h per second, S
S(12) = 18*12 = 216m/h
The “luminous flux,” or perceived brightness, of a light source is measured in lumens and is inversely proportional to the square of the distance from the light. If a light source produces 200 lumens at a distance of 3 meters, at what distance will the light source produce a luminous flux of 25 lumens?
We know that…
200*3^2 = 25 * D2^2
1800 = 25 * D2^2
1800/25 = D2^2
72 = D2^2
D2 = √72
A strain of bacteria multiplies such that the ratio of its population in any two consecutive minutes is constant. If the bacteria grows from a population of 5 million to a population of 40 million in one hour, by what factor does the population increase every 10 minutes?
We know that the 40m/5m = 8. So it increases by 8x in 60 minutes.
(60)√8 = (60)√2^3 = (20)√2 is for 1 minute.
we have 10 minutes so….
(20)√2^10 = √2.
After 2*10 minutes (20 minutes) it will have increased by √2*√2 = a factor of 2.
If a and b are integers and -4 < a < 3 and -4 < b < 5, what is the maximum possible value for a*b?
Look at the extremes…
3*5 = 15
vs.
-4*-4 = 16
Is m*n > -12?
- m > -3
- n > -4
- m > -3 NS
- n > -4 NS
Together we still don’t know as we can both take -3*10 and get -30 or… 4*5 and get 20.
If 4/x < - ⅓ , what is the possible range of values for x?
4/x must be < -⅓
-12 < x < 0
If 4/x < ⅓ , what is the possible range of values for x?
x > 12 OR…
x < 0
Is x < y?
- 1/x < 1/y
- x/y < 0
- 1/x < 1/y… from this x can either be a positive larger than y (+x > +y = ¼ < 1/2) OR a negative -x < y (1/-1) < ½
- From this we know that one of the numbers must be negative but that alone is not sufficient
Together we know that one number must be negative - either x or y is negative AND that number must be x because the reciprocal of x (1/x < 1/y).
Thus we know that x (being negative) is < y (positive) = C.
John is 20 years older than Brian. Twelve years ago, John was twice as old as brian. How old is Brian?
J = B + 20
J - 12 = 2(B-12)
B + 20 - 12 = 2B - 24
32 = B
Caleb spends $72.50 on 50 hamburgers for the marching band. If single burgers cost $1.00 each and double burgers cost $1.50 each, how many double burgers did he buy?
Number of DoubleBurgers = D
D + S = 50
1*S + 1.5*D = 72.50
S = 50 - D
1(50-D) + 1.5*D = 72.5
- D + 1.5D = 72.5 - 50
0. 5D = 22.5
D = 45
United Telephone charges a base rate of $10.00 for service, plus an additional charge of $0.25 per minute. Atlantic Call charges a base rate of $12.00 for service, plus an additional charge of $0.20 per minute. For what number of minutes would the bills for each telephone company be the same?
10 + 0.25m = 12 + 0.20m
- 25m-0.20m = 2
- 05m = 2
m = 40
Carina has 100 ounces of coffee divided into 5- and 10-ounce packages. If she has 2 more 5-ounce packages than 10-ounce packages, how many 10-ounce packages does she have?
5*A + 10*B = 100
A = B + 2
5(B+2) + 10B = 100
15B = 90
B = 6
A = 6+2 = 8
Martin buys a pencil and a notebook for 80 cents. At the same store, Gloria buys a notebook and an eraser for $1.20, and Zachary buys a pencil and an eraser for 70 cents. How much would it cost to buy three pencils, three notebooks, and three erasers? (Assume that there is no volume discount.)
What is 3P + 3N + 3E?
P + N = $0.80
E + N = $1.20
P + E = $0.70
2P + 2N + 2E = $2.70
1.5(2P + 2N + 2E) = $2.70 * 1.5 = $4.05
Andrew will be half as old as Larry in 3 years. Andrew will also be one-third as old as Jerome in 5 years. If Jerome is 15 years older than Larry, how old is Andrew?
Find A?
- Andrew will be half as old as larry in 3 years… 2(A+3) = (L+3)
- Andrew will also be one-third as old as Jerome in 5 years… 3(A+5) = J+5
- Jerome is 15 years older than Larry….. J = L + 15
2A + 6 = L + 3
3A + 15 = L + 20
difference is…
A + 9 = 17
A = 8
A circus earned $150,000 in ticket revenue by selling 1,800 V.I.P. and Standard tickets. They sold 25% more Standard tickets than V.I.P. tickets. If the revenue from Standard tickets represents one-third of the total ticket revenue, what is the price of a V.I.P. ticket?
Find PRICE of VIP?
V + S = 1800
P1*V + P2 * S = 150,000
S = 5/4*V or… V = ⅘*S
⅘*S + S = 1800
S = 1800/1.8 = 1,000
Then… V = 1800 - 1000 = 800.
P1*800 + P2*1000 = 150,000.
S*P2 = ⅓ * 150,000
S*P2 = 50,000
then…
P2 = 50,000 / 1000 = 50.
P1*800 + 50*1000 = 150,000
P1*800 = 100,000
P1 = 100,000 / 800 = $125.
Bookshelf holds both paperback and hardcover books. The ratio of paperback books to hardcover books is 22 to 3. How many paperback books are on the shelf?
- The number of books on the shelf is between 202 and 247, inclusive.
- If 18 paperback books were removed from the shelf and replaced with 18 hardcover books, the resulting ratio of paperback books to hardcover books on the shelf would be 4 to 1.
- 22+3 = 25 so… 200, 225, 250 are possible solutions. Only 225 is within 202-247.
- 225/25 = 9…. so paperbook = 9*22 = 198 = SUF
- P/H = 22/3… and (p-18)/(h+18) = 4/1 …. we have two equations and can solve so SUF
- (p-18) = 4((3p/22)+18)
- p-18 = 6p/11+ 72
- p-6p/11 = 90
- 11p/11 - 6p/11 = 90
- 5p/11 = 90
- p = (90*11)/5 = 198
On the planet Flarp, 3 floops equal 5 fleeps, 4 fleeps equal 7 flaaps, and 2 flaaps equal 3 fliips. How many floops are equal to 35 fliips?
3FLOOPS = 5 FLEEPS
4FLEEPS = 7 FLAAPS
2 FLAAPS = 3 FLIIPS
35FLIIPS in FLOOPS is…
35/1 * ⅔ * 4/7 * ⅗ = (35*24) / (3*7*5) = 24/3 = 8
Harvey runs a 30-mile course at a constant rate of 4 miles per hour. If Clyde runs the same track at a constant rate and completes the course in 90 fewer minutes, how fast did Clyde run?
Imagine that two people are 14 miles apart and begin walking towards each other. Person A walks 3 miles per hour, and Person B walks 4 miles per hour. How long will it take them to reach each other?
They move closer to each other by 3+4mp/h = 7mph
so… 14i / 7 = 2 hours.
Car X is 40 miles west of Car Y. Both cars are traveling east, and Car X is going 50% faster than Car Y. If both cars travel at a constant rate and it takes Car X 2 hours and 40 minutes to catch up to Car Y, how fast is Car Y going?
If Lucy walks to work at a rate of 4 miles per hour, but she walks home by the same route at a rate of 6 miles per hour, what is Lucy’s average walking rate for the round trip?
Machine A fills soda bottles at a constant rate of 60 bottles every 12 minutes and Machine B fills soda bottles at a constant rate of 120 bottles every 8 minutes. How many bottles can both machines working together at their respective rates fill in 25 minutes?
Alejandro, working alone, can build a doghouse in 4 hours. Betty can build the same doghouse in 3 hours. If Betty and Carmelo, working together, can build the doghouse twice as fast as Alejandro, how long would it take Carmelo, working alone, to build the doghouse?
Carmelo alone?
Alejandro = 4 hours
Betty =3 hours
Betty + Carmelo = half the time of Alejandro
¼ A, ⅓ b, 1/c
⅓ + 1/c = 2 (¼)
1/c = ½ - ⅓ = 1/6
c = 6
The population of a certain type of bacterium triples every 10 minutes. If the population of a colony 20 minutes ago was 100, in approximately how many minutes from now will the bacteria population reach 24,000?
20 minutes ago = 100
10 minutes ago = 300
NOW = 900
in 10 minutes = 2700
in 20 minutes = 8100
in 30 minutes = 24,300
The population of grasshoppers doubles in a particular field every year. Approxi mately how many years will it take the population to grow from 2,000 grasshoppers to 1,000,000 or more?
NOW = 2,000
1y = 4,000
2y = 8,000
3y = 16,000
4y = 32,000
5y = 64,000
6y = 128,000
7y = 256,000
8y = 512,000
9y = 1,024,000
Two hoses are pouring water into an empty pool. Hose 1 alone would fill up the pool in 6 hours. Hose 2 alone would fill up the pool in 4 hours. How long would it take for both hoses to fill up two-thirds of the pool?
An empty bucket being filled with paint at a constant rate takes 6 minutes to be filled to 7/10 of its capacity. How much more time will it take to fill the bucket to full capacity?
Twelve identical machines, running continuously at the same constant rate, take 8 days to complete a shipment. How many additional machines, each running at the same constant rate, would be needed to reduce the time required to complete a shipment by 2 days?
Al and Barb shared the driving on a certain trip. What fraction of the total distance did Al drive?
- Al drove for 3/4 as much time as Barb did.
- Al’s average driving speed for the entire trip was 4/5 of Barb’s average driving speed for the trip.
- not sufficient as we only know Time (not rate)
- not sufficient as we only know RATE (not time)
Together is sufficient as we know both time and rate.
Sam earned a $2,000 commission on a big sale, raising his average commission by $100. If Sam’s new average commission is $900, how many sales has he made?
A mixture of “lean” ground beef (10% fat) and “super-lean” ground beef (3% fat) has a total fat content of 8%. What is the ratio of “lean” ground beef to “super lean” ground beef?
Ratio of LEAN to SUPER LEAN?
10-8 = +2
3-8 = -5
Lean(+2) + SUPER-LEAN(-5) = 0 … (now just pick values for x and y such that the equation will equal 0).
5(+2) + 2(-5) = 0
10 - 10 = 0
In a group of men and women with a ratio of 2:3, the men have an average age of 50 and the average age of the group is 56. What is the average age of women?
men 2 : women 3
overall = 56 years
men = 50 years
women = ?
2(56-50) + 3(w) = 0
-12 + 3w = 0
w = 4
women have a +4 differential and must be 56+4 = 60 years old.
The average of 11 numbers is 10. when one number is eliminated, the average of the remaining numbers is 9.3. What is the eliminated number?
A = s/n
10 = s /11
s = 110
9.3 = s/(11-1)
s = 93
110 - 93 = 17
Given the set of numbers {4,5,5,6,7,8,21}, how much higher is the mean than the median?
the mean is (4+5+5+6+7+8+21) /7 = 56 / 7 = 8
the median is 6 as it is the middle number.
8-6 =2
A charitable association sold an average of 66 raffle tickets per member. Among the female members, the average was 70 raffle tickets. The male to female ratio of the association is 1:2. What was the average number of tickets sold by the male members of the association?
66 = s/n
female = 70 = s/n
Male 1, Female 2…. 1:2
female = 70-66 = 4
1(m) + 2(4) = 0
m = -8
66-8 = 58.
Matt gets a $1,000 commission on a big sale. This commission alone raises his aver age commission by $150. If Matt’s new average commission is $400, how many sales has Matt made?
If the average of x and y is 50,and the average of y and z is 80, what is the value of z-x ?
(x+y)/2 = 50
(y+z)/2 = 80
x+y = 100
and
y+z = 160
y+z-(x+y) = 160-100
z-x = 60
On a particular exam, the boys in a history class averaged 86 points and the girls in the class averaged 80 points. If the overall class average was 82 points, what was the ratio of boys to girls in the class?
Find the ratio of boys to girls…
Boys = 86 = s/n
Girls = 80 = s/n
Overall = 82 = s/n
Boys… 86 - 82 = 4
Girls… 80 - 82 = -2
b(4) + g(-2) = 0
b = 1, g = 2,
1:2
(9,12,15,18,21}
Which of the following pairs of numbers, when added to the set above, will increase the standard deviation of the set?
- 14, 16
- 9, 21
- 15, 100
Note first that the mean = 15.
- 14, 16 will NOT.. actually decrease SD
- 9, 21 will increase SD
- 15, 100 will increase SD substantially
2 and 3.
What is the sum of all the positive integers up to 100 inclusive?
((100-1)+1)/2 = 101/2 = 50.5
100-1+ 1 = 100 numbers
50.5 * 100 = 5,050
In a sequence of 8 consecutive integers, how much greater is the sum of the last four integers than the sum of the first four integers?
A, B, C, D, E, F, G, H
Every number of the 4 last are exactly 4 bigger than the same position of the first four.
(E+F+G+H) - (A+B+C+D) = 4*4 = 16 higher.
How many terms are there in the set of consecutive integers from -18 to 33 inclusive?
33 + 18 + 1 = 52
If the sum of the last 3 integers in a set of 7 consecutive integers is 258, what is the sum of the first 4 integers?
A, B, C, D, E, F, G
258/3 = 86.
thus.. F = 86.
81, 82, 83, 84, 85, 86(F), 87
The first four is A+B+C+D = 81+82+83+84 = 320+10 = 330.
Of 28 people in a park, 12 are children and the rest are adults. 8 people have to leave at 3pm; the rest do not. If after 3pm, there are 6 children still in the park, how many adults are still in the park?
Of 30 snakes at the reptile house, 10 have stripes, 21 are poisonous, and 5 have no stripes and are not poisonous. How many of the snakes have stripes AND are poisonous?
Students are in clubs as follows: Science-20, Drama-30, and Band-12. No student is in all three clubs, but 8 are in both Science and Drama, 6 are in both Science and Band, and 4 are in Drama and Band. How many different students are in at least one of the three clubs?
ScienceT=20
DramaT=30
BandT = 12
in at least in club?
In all three = 0
in drama+science = 8
in science+band = 6
in band+drama=4
ScienceAlone = 20 - 8 -6 = 6
DramaAlone = 30 - 8 - 4 = 18
BandAlone = 12 - 6 -4 = 2
All together…. 6 + 18 + 2 + 0 + 8 +6 +4 = 44
Of 60 children, 30 are happy, 10 are sad, and 20 are neither happy nor sad. There are 20 boys and 40 girls. If there are 6 happy boys and 4 sad girls, how many boys are neither happy nor sad?
A car travels from Town A to Town B at an average speed of 40 miles per hour, and returns immediately along the same route at an average speed of 50 miles per hour. What is the average speed in miles per hour for the round-trip?
a, b, and c are integers in the set {a, b, c, 51,85,72}. Is the median of the set greater than 70?
- b > c > 69.
- a < c < 71
- b>c>69… then we know that (a, 51, c, 72, b, 85) and c is minimum 70. (70+72)/2 > 70. Sufficient
- a<c></c>
</c>
A store sells chairs and tables. If the price of 3 chairs and 1 table is 60% of the price of 1 chair and 3 tables, and the price of 1 table and 1 chair is $60, what is the price, in dollars, of 1 table? (Assume that every chair has the same price and every table has the same price.)
- 15
- 20
- 30
- 40
- 45
3*c + 1*t = 0.6(1*c+3*t)
1*c+1*t = 60
From this we know immediately that T is bigger than c.
We can thus rule out all other options than d=40 and e=45 for T.
Thus, we test one of them….
if t = 45, then c = 60-45 = 15
3*15 + 1*45 = 0.6(1*15+3’45)
90 = 0.6*150
true.
T = 45
Boys and girls in a class are writing letters. There are twice as many girls as boys in the class, and each girl writes 3 more letters than each boy. If boys write 24 of the 90 total letters written by the class, how many letters does each boy write?
Orange Computers is breaking up its conference attendees into groups. Each group must have exactly one person from Division A, two people from Division B, and three people from Division C. There are 20 people from Division A, 30 people from Division B, and 40 people from Division C at the conference. What is the smallest number of people who will not be able to be assigned to a group?
First figure out which group is the limiting factor…
Division A = 20/1 = 20 groups possible
Division B = 30/2 = 15 groups possible
Division C = 40/3 = 13 groups possible
So we get maximum 13 groups where the unassigned people will be…
Division A = 20-13*1 = 7 persons
Division B = 30-13*2 = 4 persons
Division C = 40-3*13 = 1 person
Minimum 12 unassigned employees.
Velma has exactly one week to learn all 71 Japanese hiragana characters. If she can learn at most a dozen of them on any one day and will only have time to learn four of them on Friday, what is the least number of hiragana that Velma will have to learn on Saturday?
71 - 4 = 67 for six days
Max 12 a day = (6-1)*5 = 60.
67-60 = 7 minimum on Saturday
A “Collector’s Coin Set” contains a one dollar coin, a fifty-cent coin, a quarter (= 25 cents), a dime (= 10 cents), a nickel (= 5 cents), and a penny (= 1 cent). The Coin Sets are sold for the combined face price of the currency. If Colin buys as many Coin Sets as he can with the $25 he has, how much change will Colin have left over?
- 00
- 50
- 25
- 10
- 05
- 01
= 1.91.
25 / 1.91….
- 10 (10 sets)
- 73 (3 sets)
- 83 so 17 cents left.
What can be said about the SUM of a set of consecutive integers in terms of divisibility?
- For any set of consecutive integers with an ODD number of items, the sum of all the integers is ALWAYS a multiple of (and thus divisible by) the number of items
- For any set of consecutive integers with an EVEN number of items, the sum of all the items is NEVER a multiple of the number of items.
If r, s, and t are consecutive positive multiples of 3, is rst divisible by 27,54, or both?
BOTH…
r, s and t are all multiples of 3. thus, the product of r*s*t must have THREE 3s as factors AND at least one of the numbers will be EVEN so the product will also have 2 as a factor.
Is the sum of the integers from 54 to 153 inclusive divisible by 100?
NO
There are 100 integers from 54 to 153 (153-54+1 = 100).
For any EVEN number of consecutive integers, the sum of all the integers is NEVER a multiple of the number of integers.
thus, the sum of the integers from 54 to 153 will not be divisible by 100.
A machinist’s salary at a factory increases by $2,000 at the end of each full year the machinist works. If the machinist’s salary for the fifth year is $39,000, what is the machinist’s average annual salary for his first 21 years at the factory?
$2,000 increments
y5 = $39,000
y1 = $39,000 - 4*2,000 = $31,000
t21 = $39,000 + 16*2,000 = $71,000
($71,000 + $31,000) / 2 = $51,000 average salary.
Is the average of n consecutive integers equal to 1?
- n is even.
- If S is the sum of the n consecutive integers, then 0 < S < n.
- It tells us that there is an EVEN number of consecutive integers and we know that the average of an even number of consecutive integers NEVER will be an integer, so this is actually SUFFICIENT although we know nothing about the numbers
- Knowing A = s/n and that s<n></n>
</n>
