Geometry (Triangles Pt. 2) Flashcards
(26 cards)
Sine (Definition)
The trigonometric function that is equal to the ratio of the side Opposite an acute angle (In a right triangle) to the Hypotenuse.
“SOH”
*Use this equation if the side is far away from the angle
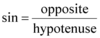
Cosine (Definition)
The trigonometric function that is equal to the ratio of the side Adjacent to an acute angle (in a right triangle) to the Hypotenuse.
“CAH”
*Use this equation if the side is close to the angle
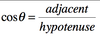
Tangent (Definition)
The trigonometric function that is equal to the ratio of the side Opposite to an acute angle (in a right triangle) to the Adjacent.
“TOA”
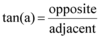
What is the Sin, Cos, and Tan of angle “F.”
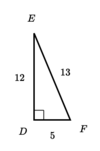
Sin (F) = 12/13
Cos (F) = 5/13
Tan (F) = 12/5
What is the Sin, Cos, and tan of angle “G.”
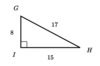
Sin (G) = 15/17
Cos (G) = 8/17
Tan (G) = 15/8
Find the Cos of angle “A.”
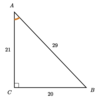
21/29
Tips for solving missing sides of a triangle
- If the missing side is the hypotenuse, divide the given side by the Trig ratio.
- If given the Hypotenuse, multiply the Trig ratio by the other given side.
- If using the Tangent Function and the Opposite is given, divide by the Trig ratio.
- If using the Tangent Function and the Adjacent is given, multiply the Trig Ratio by the other given side.
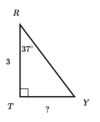
Find the missing side of the triangle
Round your answer to the nearest hundredth.
6.97
Find the missing sides of the triangle
Round your answer to the nearest hundredth.

x = 8.62
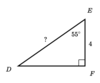
Find the missing side of the triangle
Round your answer to the nearest hundredth.
2.26
Find the missing angle of the triangle
Round your answer to the nearest hundredth.
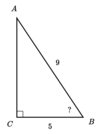
56.25°
Find the missing angle of the triangle
Round your answer to the nearest hundredth.
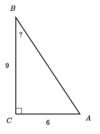
33.69º
Find the missing angle of the triangle
Round your answer to the nearest hundredth.
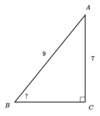
51.06°
Define the Law of Sines
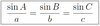
Tips for solving using the Law of Sines
- When finding the missing angle, arcsine (Side correseponding to the missing Angle/ given side) Sine (Given angle)
- When finding the missing side, multiply the given side by the Sine of the angle corresponding to the missing side, then divide by the Sine of the given angle.
Find the missing angle “B”.

53.68°
Find the missing side “AB”.

7.71
Find the missing angle “B”.

60.76°
Find the missing side “AC”.

9.23
Create a proof for the Law of Sines
- Create a triangle that doesn’t have a 90°
- Label two sides and angles opposite each other.
- Drop an altitude through the middle of the two sides and angles.
- Create two equation using the two angles as a function of Sine.
- Solve and simplify the two equations as a single equation for the new side “x”.
Define the Law of Cosines
* The side opposite the given angle is
(The missing side squared =
side b (squared) + side c (squared) - 2(bc)cos(σ)

Find the missing side “AB”

18.03
Find the missing side “BC”.

14.62
Find the missing angles

angle “A” = 48.37°
angle “B” = 55.30°
angle “C” = 76.33°


