Geometry (Circles Part. 3) Flashcards
(7 cards)
1
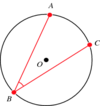
Q
Inscribed Angle
A
The angle subtended at a point on the circle by two given points on a circle.
2
Q
Inscribed Angle Theorem
A
States that an angle “ψ” inscribed in a circle is half of the Central Angle (Ø) that subtends the same arc of the circle.
I.E. “ψ = Ø/2”
3
Q
What is the measure of Angle (ABC) in degrees?
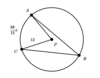
A
34°
4
Q
What is the length of Arc (AC)?
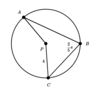
A
16π/5
5
Q
Prove the Inscribed Angle Theorem for Case: A.
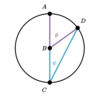
A
- Spot the Isoceles Triangle and label the two congruent angles as ψ.
- Label the missing inscribed angle as: (180° - Ø) because an angle of a straight line is equal to 180°.
- Create equation: ψ + ψ + 180° - Ø = 180°
- Simplify the equation to receive the theorem: “ψ = Ø/2”
6
Q
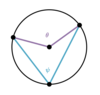
Prove the Inscribed Angle Theorem for Case: B.
A
- Draw a diameter that goes through the Central Angle and the Inscribed Angle.
- Split the two sets of angles created as ψ1 + ψ2 and Ø1 + Ø2.
- Now we have two sets of the same situation in Case: A, so we have the two equations: Ø1 = 2ψ1 and Ø2 = 2ψ2.
- We add both equations, substitute (Ø1 + Ø2) = Ø and
(ψ1 + ψ2) = ψ to get “ψ = Ø/2”
7
Q
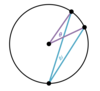
Prove the Inscribed Angle Theorem for Case: C.
A
- Create a diameter and label the parts
- Because of Case: A, we know that Ø2 = 2ψ.
- We combine all the angles created to get:
Ø2 + Ø = 2ψ2 + 2ψ
- We substitue Ø2 = 2ψ to get:
2ψ + Ø = 2ψ2 + 2ψ
- Simplify to get:
Ø = 2ψ2



