Geometry (Circles Part. 2) Flashcards
Arc Length
(Definition)
A portion of the circumference of the circle.
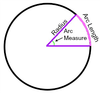
Explain how you get the Arc Length (Degrees) Equation
- You need the central angle that subtends the arc length.
- From there, you can divide that angle (In degrees) by (360°) to receive the ratio of the Arc Length in comparison to the entire Circumference.
- Then, you multiply the ratio of the Arc Length and the Circumference to receive the total Arc Length
* From that information, you can create and manipulate the equation to determine the Arc Measure or Circumference of a Circle (In degrees)
Arc Length
(Degrees Equation)
Arc Length = (Central Angle/ 360°) Circumference
In the figure below, line (DB) and (AC) are diameters of circle P. The length of line (PB) is 8 units.
What is the length of curve (DC)?
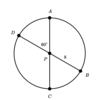
(16/3)π
or
16.76
In the figure below, line (BC) is a diameter of circle P. The length of line (BP) is 3 Units.
What is the length of curve (ACD)?
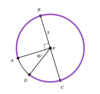
(65/12)π
or
17.02
In the figure below, angle (APB) ≈ angle (BPC). The length of line (PB) is 4 units.
What is the length of curve (BC)?
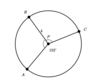
(104/45)π
or
7.26
Central angle
(Equations)
Central Angle = (Arc length/ Circumference) (360°)
In the figure below, the radius of circle p is 10 units. Arc (ABC) has a length of 16π.
What is the measure of Arc (AC), in degrees?
72°
In the figure below, the radius of circle P is 18 units. The length of Arc (BA) is 14π.
What is the measure of Arc (BC) in degrees?
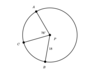
64°
Circumference (From Arc Length and Central Angle)
(Equations)
Circumference = (360° / Central Angle) (Arc Length)
Degree
(Definition)
A unit of measurement of angles, equal to 1/360 of the circumference of a circle.
Radian
(Definition)
Describes the plane angle subtended by a circular arc as the length of the arc divided by the radius of the arc.
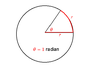
Explain how you get the Equation to convert (Radians to Degrees)
360 (Degrees) = Circumference
2π (Radians) = Circumference
360 (Degrees) = 2π (Radians)
180 (Degrees) = π (Radians)
180/π (Degrees) = (Radians)
Radian to degrees
(Equation)
1 Radian = (180/π) Degrees
Convert the angle Ø = (23π/20) radians to degrees.
207°
Convert the angle Ø = (8π/9) radians to degrees.
160°
Convert the angle Ø = (17π/18) radians to degrees.
170°
Degree to Radians
(Equation)
1 Degree = (π/180) Radians
Convert the angle Ø = 290° to radians.
29π/18 Radians
Convert the angle Ø = 260° to radians.
13π/9 Radians
Convert the angle Ø = 100° to radians.
5π/9 Radians
Explain how you get the Arc Length Equation in Radians.
- We established the Arc Length (Degree Equation) to be
Arc Length = (Central Angle/ 360°) (Circumference)
- We can substitue (360-Degrees) with (2π-Radians).
- We also substitute the (Circumference) with (2πr)
- The new equation we get is
Arc Length = (Central angle/ 2π) (2πr)
- Then we simplify (Central angle x 2πr) / (2π) to get
Arc Length = Central Angle x Radius
Arc Length
(Radian Equation)
Arc Length = Arc Measure (Radians) x Radius
What is the exact length of Curve (BCA)?
85π/2
What is the exact length of Curve (DAC) on Circle P?
5π
What is the exact length of Curve (CD)?
35π/18
Arc Measure
(Radian Equation)
Arc Measure = Arc Length/ Radius
What is the arc measure of Curve (AB), in radians?
17π/30
What is the arc measure of Curve (CD), in radians?
π/5
What is the arc measure of Ø in radians?
7π/6
Area of a circle
(Equation)
Area of a circle = πr2
What is the area of the Sector?
27π
What is the area of the Sector?
45π/4
What is the area of the Circle?
9π
What is the area of the Sector?
45π/4
