Geometry (Triangles) Flashcards
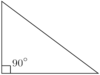
Right Triangle
A Triangle with a “right” or 90° angle.
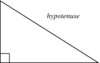
Hypoteneus
The longest side of a right triangle, opposite the right angle.
Pythagorean Theorem
a2 + b2 = c2
- In a Right Triangle, the area of the square whose side is the “hypotenuse” is equal to the sum of the areas of the squares of the other two sides.
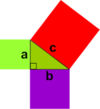
Describe Garfields Proof of the Pythagorean Theorem
- Construct a right triangle with Length “B,” Height “A,” and Hypotenuse “C.”
- Create a Congruent Triangle (Stacked on Top) creating a side “A + B” as the height.
- Label the Angles and Prove that the missing Angle = 90°.
- Create an equation using the Area of a Trapezoid,
Height x ((Top Base + Bottom Base)/ 2)
- Create an equation using the Area of the Triangles,
(Base x Height) / 2 and simplify both as a single equation.
Find the “x” value in the triangle below.
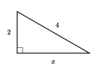
2√3
Find the x value in the triangle below.
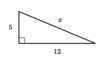
x = 13
Find the x value in the triangle below.
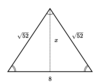
x = 6
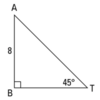
Find the x value in the triangle below.

x = 8
45°-45°-90° Triangle Equation for the Hypotenuse
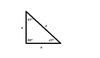
A = B = (√2/2) C
or
(√2) A = (√2) B = C
Find the length of the unknown sides in the triangle shown below
8√2
Find the length of the unknown sides in the triangle shown below
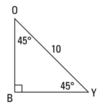
5√2
Create a Proof for the 45°-45°-90° Triangle Equation
- Establish that a 45°-45°-90° Triangle has two equal length sides.
- From that information we can Establish that in the Pythagorean Theorem, A = B, and we can Substitute one with the other.
- Simplify the equation and solve for A or B to determine that
A = B = (√2/2) C
or
(√2) A = (√2) B = C
Destinguishing a 45° 45° 90° Triangle
- The two sides that aren’t the hyptotenuse will be the same length
- When given the hypotenuse, the other side of the triangle will be half the length of the Hypotenuse multiplied by √2.
- To find the hypotenuse just multiply the a leg of the Triangle by √2.
Destinguishing the three sides of a 30° 60° 90° Triangle
- The side opposite the 90° angle is equal to “x.”
- The side opposite the 30° angle is 1(x)/2.
- The side opposite the 60° angle is √3(x)/2.
Create a proof for the sides of a 30° 60° 90° Triangle.
- Create an Equilateral Triangle and label all the sides and angles.
- Split the Equilateral Triangle down the middle and label the new sides and angles.
- Create an equation using the Pythagorean Theorem to find the missing side.
- Solve and Simplify the equation for the missing side “a.”
Solve for the missing side of the Triangle.

6√3
Solve for the missing Sides.
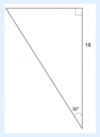
Hypotenuse = 12√3
Side B (opposite 30° angle) = 6√3
Solve for the missing Sides.
Side (opposite 60°) = 15√3
Side (opposite 30°) = 15
How can you destinguish a 30° 60° 90 °Triangle?
The Hypotenuse will either be (The length of the shortest side multiplied by 2) or (The length of the second longest side divided by √3 then multiplied by two).
The second longest side (opposite the 60° angle) will either be (The length of the shortest side multiplied by √3) or (The length of the hypotenuse divided by two, then multiplied by √3).
The shortest length (opposite the 30° angle) will either be (The length of the hypotenuse divided by 2) or (The length of the second longest side divided by √3).
How do you find the area of a Triangle?
Multiply the base of the Triangle by the height, then divide by 2.



