Free and Forced Vibrations 16-17 Flashcards
What is a free vibration?
A spring vibrating in air.
What formula gives the total energy of a freely oscillating mass on a spring?
Etotal= 1/2mv2 + 1/2Kx2
(in other words, K.E + P.E)
A system can be forced to vibrate by a periodic external force.
The fequency of this force is called what?
Driving frequency.
When does a system resonate?
When the driving frequency approaches the natural frequency, the system gains more and more energy from the driving force and so vibrates with a rapidly increasing amplitude. When this happens the system is resonating.
Give examples of resonance.
1) The column of air resonates in an organ pipe, driven by the motion of air at the base.
2) A swing resonates if it’s driven by someone pushing it at its natural frequency.
3) A glass resonates when driven by a sound wave at the right frequency.
4) A radio is tuned so the electric circuit resonates at the same frequency as the radio station you want to listen to.
Why are some systems designed to experience damping forces?
Systems are often deliberately damped to stop them oscillating or to minimise the effect of resonance.
Given an example of a system in cars that uses damping.
Shock absorbers in a car suspension provide a damping force by squashing oil through a hole when compressed.
Draw a graph of light damping in an oscillating system.

Draw a graph of heavy damping in an oscillating system.

Draw a graph of critical damping.
- Critical damping reduces the amplitude ( stopts the system oscillating) in the shortest possible time.
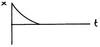
Draw a graph of an overdamped oscillating system.
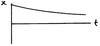
Why are car suspension systems and moving coil meters critically damped?
They are critically damped so that they don’t oscillate but return to equilibrium as quickly as possible.
Why do lightly damped systems have a sharp resonance peak?
Their amplitude only increases dramatically when the driving frequency is very close to the natural frequency.
Why do heavily damped systems have a flatter response?
Their amplitude doesn’t increase very much near the natural frequency and they aren’t as sensitive to the driving frequency.
Draw the amplitude vs frequency of lightly damped oscillating systems and heavily damped oscillating systems.



