ERM Ch.3

Question 1

IRM Components

Answer 1

• Startup: Staffing & Scope
• Parameter Development
• Implementation
• Integration & Maintenance

Question 2

Startup: Staffing & Score Components

Answer 2

Question 3

Parameter Development Components

Answer 3

• Modeling software – Assess the capabilities of the modeling software available, and make sure it matches capabilities of the IRM team
• Parameter Development – include expertise from Underwriting, Planning, Claims and Actuarial. Develop a systematic way to capture expert opinion
• Correlation – have the IRM team recommend correlations. This needs to be owned at a high level (CEO,CRO,CUO), since it crosses lines of business, and has a significant impact on the allocated capital.
• Validation‐ Validate and test over an extended period. Provide training, so that interested parties all have a basic understanding of the statistics

Question 4

Implementation Components

Answer 4

• Priority Setting – have top management set the priority for implementation
• Communications – Regular communication and to a broad audience
• Pilot Testing – allows effective preparation of the company for the magnitude of the change
• Education – training so leadership has a similar base level of understanding

Question 5

Integration & Maintenance Components

Answer 5

• Cycle – Integrate into planning calendar
• Updating – Major input review should be no more than twice a year; minor updates can be handled by modifying the scale of the impacted portfolio segments
• Controls – Maintain centralized control of inputs, outputs and even application templates

Question 6

Coefficient of Variation of the total losses

Answer 6

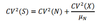
Question 7

Two ways to estimate Projection Risk

Answer 7

• Simple Trend Model
• Trend as a Time Series

Question 8

Estimation Risk

Answer 8

• Parameters are often estimated using the MLE
  
  • Lowest estimation error of unbiased estimators
• Work with the negative of the second derivative of the log likelihook (information matrix - inverse of the covariance matrix)
  
  • Slope is steep near the MLE - high confidence

Question 9

Why Joint LogNormal? (Small dataset problems)

Answer 9

• Standard deviations may be large ->Significant probability of having parameters w/ negative values
• For heavy tail distributions,, the parameters themselves are heavy tailed

Question 10

Model Risk - Selecting the best distribution

Answer 10

• Use the Hannan-Quinn Information Criterion (HQIC)
• It is a compromise of other information criteria which add larger or smaller penalties

Question 11

Select paramters for model risk

Answer 11

• Randomly select a mean for alpha and beta, and a covariance matrix from a pool of disributions you have selected
• Now that you’ve selected a distribution for alpha and beta, randomly draw an alpha0 and beta0
• For each claim that is simulated, draw from the distribution with parameters (alpha0,beta0)

Question 12

Kendall’s t

Concordant

Discordant

Answer 12

• t = (C-D)/# of pairs
• Concordant:
  
  • x1>x2 and y1>y2 or vice versa
• Discordant:
  
  • Mixed
• Focuses on rank of each data point not on its value

Question 13

Frank’s Copula

Answer 13

• Small tail dependencies

Question 14

Gumbel’s Compula

Answer 14

• More probability in the tails
• More density in the right tail
• t(a) = 1- (1/a)

Question 15

Heavy Right Tail (HRT) Copula

Answer 15

• Less correlation in the left tail, but high correlation in the right tail
• t(a) = 1/(2a+1)

Question 16

Normal Copula

Answer 16

• Joins two distributions using the correlations from the bivariate normal
• More dependencies in the tail
• Symmetrical
• t(a) = 2arcsin(a)/pie

Question 17

Tail Concentration Function - L & R

Answer 17

• L(z) = c(z,z)/z
• R(z) = (1 - 2z + C(z,z))/(1-z)