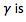chapter 6 Flashcards
A flow is hydrodynamically unstable if
a small perturbation in the flow grows spontaneously, drawing energy from the mean flow.
It is useful to divide fluid instabilities into two types:
parcel instability and wave instability
Examples of parcel instability are
buoyant instability and inertial instability.
Buoyant Instability
If the atmospheric lapse rate (Γ) is more than the dry adiabatic lapse rate (Γ), an air parcel displaced upward will become buoyant and tend to move away from to its original level.
Inertial Instability
If an air parcel that is moving with the zonally directed geostrophic basic flow, is displaced across the stream, will accelerate further from that position
In buoyant and inerital instability an air parcel moved from its original position will
continue to accelerate away from where it started, instead of oscillating around its original position.
Most of the instabilities of importance in meteorology, are associated with
wave propagation
The wave instabilities important for synoptic-scale meteorology generally occur in the form of
perturbations to a zonally symmetric basic flow field
A
B
C
D
In general the basic flow is
a jetstream that has both horizontal and vertical mean-flow shears.
Examples of wave instability are:
barotropic and baroclinic instability.
Barotropic Instability is
a wave instability associated with the horizontal shear in a jet-like current.
Barotropic instabilities grow by
extracting kinetic energy from the mean-flow
Baroclinic instability, is associated with
vertical shear of the mean flow.
Baroclinic instabilities grow by
converting potential energy associated with the mean horizontal temperature gradient that must exist to provide thermal wind balance for the vertical shear in the basic state flow.
Wave Instability Assessment
Step 1:
Wave Instability Assessment
Step 2:
Wave Instability Assessment
Step 3:
Wave Instability Assessment
Step 4:
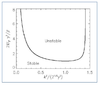
If N is real then the fluid is
stable, and a parcel disturbed vertically from rest would oscillate about its original position.
If N is real then the fluid is stable, and a parcel disturbed vertically from rest would oscillate about its original position. However, if N is imaginary then
we know a parcel will be unstable
If N is real then the fluid is stable, and a parcel disturbed vertically from rest would oscillate about its original position. However, if N is imaginary then we know a parcel will be unstable, and if perturbed from rest it will
accelerate away from its original position.
If N is real then the fluid is stable, and a parcel disturbed vertically from rest would oscillate about its original position. However, if N is imaginary then we know a parcel will be unstable, and if perturbed from rest it will accelerate away from its original position.
This can also be seen from
the dispersion relation, since N will be imaginary, and hence w will have an imaginary component.
One form of ………………………………… that can occur in the atmosphere is barotropic instability, associated with ……………………………………
hydrodynamic instability
the horizontal shear of the mean wind
This means that for barotropic instability to occur that the second derivative of the mean zonal wind must be equal
ß somewhere in the flow
We can interpret this to mean that the absolute vorticity must have a
minimum or maximum value somewhere in the flow in order for barotropic instability to occur.
……………………………………………………………….. minimum or maximum value somewhere in the flow in order for barotropic instability to occur.
We can interpret this to mean that the absolute vorticity must have a
Barotropic instability is dependent upon
horizontal shear of the mean flow
……………………………………….. is dependent upon horizontal shear of the mean flow
Barotropic instability
to examine if barotropic instability is possible, the …………………………………………… must be examined
horizontal profile of the absolute vorticity
The figure below shows the
zonal velocity, absolute vorticity and the second derivative of the velocity for an idealized westerly jet stream on the beta plane.
The dashed line on the third diagram is
the value of beta
There are ………………………………………………………. on both flanks of the jet, near the locations of ………………………………………………………………….
absolute vorticity minima and maxima
the inflection points in the velocity profile
There are absolute vorticity minima and maxima on both flanks of the jet, near the locations of the inflection points in the velocity profile.
Thus, the condition for ……………………………… is ……………………………………..
barotropic instability is met in these two regions
There are absolute vorticity minima and maxima on both flanks of the jet, near the locations of the inflection points in the velocity profile.
Thus, the condition for barotropic instability is met in these two regions.
However, the presence of an inflection point
does not automatically mean that there is a minimum or maximum in the absolute vorticity.
If beta is large compared to the second derivative of the velocity, such as for a
broad, weak jet at low latitudes
if ………………………………………………………. such as for a broad, weak jet at low latitudes
beta is large compared to the second derivative of the velocity,
If beta is large compared to the second derivative of the velocity, such as for a broad, weak jet at low latitudes, as shown in figure, then there will
not be any maxima in vorticity, even though there are inflection points in velocity profile.
If beta is large compared to the second derivative of the velocity, such as for a broad, weak jet at low latitudes, as shown in figure, then there will not be any maxima in vorticity, even though there are inflection points in velocity profile.
Thus, ……………. acts as
beta
stabilizing influencing against barotropic instability.
Barotropic disturbances derive their energy from
the mean flow
Barotropic disturbances derive their energy from the mean flow. Energy considerations show that
for a barotropic disturbance to grow it must tilt opposite to du/dy
Since midlatitude disturbances tend to ……………………………………… they actually
tilt in the same direction as du/dy they actually lose energy back to the mean flow due to barotropic instability.
Since midlatitude disturbances tend to tilt in the same direction as ⁄ they actually lose energy back to the mean flow due to barotropic instability.
Thus, barotropic instability is not a viable way for
midlatitude disturbances to form and grow.
Thus, barotropic instability is not a viable way for midlatitude disturbances to form and grow. However,
since midlatitude disturbance decay due to barotropic instability, they give up energy to the mean flow and help maintain the mean flow against friction.
hus, barotropic instability is not a viable way for midlatitude disturbances to form and grow. However, since midlatitude disturbance decay due to barotropic instability, they give up energy to the mean flow and help maintain the mean flow against friction.
Thus, barotropic instability is somewhat
important for the maintenance of the mean flow in the midlatitudes.
Since barotropic instability is not a
feasible option for the formation of midlatitude cyclones, then another mechanism that must be invoked, is the Baroclinic Instability.
For baroclinic instability it is the …………………………. rather than ………………………….. that is important
vertical shear
horizontal shear
For baroclinic instability it is the vertical shear, rather than the horizontal shear, that is important.
In an atmosphere with baroclinic instability, small random
perturbations in the turbulent flow of the atmosphere give rise to vertical displacements (warm air raising and cold air sinking).
In an atmosphere with baroclinic instability, small random perturbations in the turbulent flow of the atmosphere give rise to vertical displacements (warm air raising and cold air sinking).
Under suitable vertical wind shear, these ………………………………………… due to ………………………………………………..
vertical displacements will grow spontaneously due to conversion of potential energy to kinetic energy
Under suitable vertical wind shear, these vertical displacements will grow spontaneously due to conversion of potential energy to kinetic energy. The baroclinic instability is also ………………….. dependent
wavelength
Baroclinic instability is often studied for the simple case of
a two-layer fluid, for which waves are unstable if the following condition is true
Baroclinic instability is often studied for the simple case of a two-layer fluid, for which waves are unstable if the following condition is true:
In the above expression (Eq.3):
UT is the
vertical wind shear parameter (equal to half the difference in U between the two layers and
Baroclinic instability is often studied for the simple case of a two-layer fluid, for which waves are unstable if the following condition is true:
In the above expression (Eq.3):
inversely proportional to static stability (large stability means small ).
is the vertical wind shear parameter (equal to half the difference in U between the two layers and
is inversely proportional to static stability (large stability means small ).
The above expression points out the
importance of vertical wind shear on baroclinic instability.
There is also a ………………………. dependence for baroclinic instability
wavelength
vertical shear
wavenumber
The influence of vertical shear and wavelength on the baroclinic instability can be understood by
plotting a curve between the two
the influence of ………………………………………. on the baroclinic instability can be understood by plotting a curve between the two
vertical shear and wavelength
The above curve demonstrates that
The above curve demonstrates that for small values of shear the flow is stable, but as shear increases, instability will set in when is greater than unity.
The plot also shows that there will be
Analysis of baroclinic instability in the real (………………………………) atmosphere is much ………………………………………………
continuously stratified
more complicated than for the two-layer fluid.
Analysis of baroclinic instability in the real (continuously stratified) atmosphere is much more complicated than for the two-layer fluid.
Qualitatively the results are
similar, with instability depending on the vertical shear.
Analysis of baroclinic instability in the real (continuously stratified) atmosphere is much more complicated than for the two-layer fluid.
Qualitatively the results are similar, with instability depending on the vertical shear. However, in the real atmosphere there is always ………………………, so ………………………………
an unstable wave number, so barotropic instability is pervasive in the middle latitudes.
The amount of instability, and growth rates, increase with
the amount of wind shear and other factors.
……………………………………………………… increase with the amount of wind shear and other factors.
The amount of instability, and growth rates
Baroclinic instability in the regions of ………………………………………………… is the mechanism by which ……………………………….
strong horizontal thermal gradients
midlatitude cyclones form
Baroclinic instability in the regions of strong horizontal thermal gradients is the mechanism by which midlatitude cyclones form.
Baroclinic instability (combined with ……………………………………) is also important for the …………………………………….
barotropic instability
formation of African Easterly waves.
