chapter 5 Flashcards
we derived the QG Height Tendency Eq., the QG Omega Eq. is also derived from:
- QG Thermodynamic Energy Eq.
- QG Vorticity Eq.
In deriving the QG Height Tendency Eq., we have eliminated ……………. from the above equations
omege (w)
Now, to derive the QG Omega Eq., instead, we eliminate …………………………………. from the above two equations
the geopotential tendency (x)
Like the geopotential tendency equation, we can interpret the omega equation in a qualitative fashion by
assuming that atmospheric disturbances are sinusoidal. The LHS of the equation is then proportional to the negative of omega
………………………………………………………. assuming that atmospheric disturbances are sinusoidal. The LHS of the equation is then proportional to the negative of omega
ike the geopotential tendency equation, we can interpret the omega equation in a qualitative fashion by
describe the terms in the equation
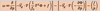
the euqaiton can be writen qualitatively as
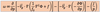
As with the ………………………., the terms on the RHS of the omega equation can be explained physically.
tendency equation
PVA increasing with height (……………………………………) results in
…………………………….
(decreasing with pressure)
upward vertical motion.
NVA increasing with height results in
downward vertical motion
…………………………… results in upward vertical motion.
PVA increasing with height (decreasing with pressure)
……………………………………… results in downward vertical motion
NVA increasing with height
Warm advection will increase …………………………………. and result in
the thickness of a layer and result in higher heights aloft compared to below
Warm advection will increase the thickness of a layer and result in higher heights aloft compared to below
This results in
divergence aloft, and convergence below
Warm advection will increase the thickness of a layer and result in higher heights aloft compared to below
This results in divergence aloft, and convergence below
This convergence/divergence pattern leads to
upward motion
Le chatelier’s principle is at work because the upward motion will lead to
adiabatic cooling
Le chatelier’s principle is at work because the upward motion will lead to adiabatic cooling, which
opposes the temperature change forced by the advection
the result of this is
The diabatic heating term has essentially the same physical explanation as the
advection term
……………………………………. has essentially the same physical explanation as the advection term
the diabatic heating term
Warming leads to …………….. motion
upward
Warming leads to upward motion, ………………… of the cause of the ………………………………..
regardless
warming (warm advection or diabatic heating.)
…………………………………………………… in the omega equation represent different physical processes
The differential vorticity advection term and the thermal advection term
The differential vorticity advection term and the thermal advection term in the omega equation represent different physical processes
They may
add or cancel each other, and so analysis of the net result is difficult.
Another useful way for diagnosing vertical motion (w) is to
derive an alternate form of the omega equation, called the Q-vector form of the equation
the Laplacian of w is equal to
twice the divergence of the Q-vector field. Because the Laplacian of w is proportional to −w
Divergence of Q vectors result in
descent
Convergence of Q vectors will result in
Ascent
forcing for descent (………………… w) is found where
positive
Q vectors diverge
forcing for ascent (…………………… w) is found where …………………………..
negative
Q vectors converge
Therefore, forcing for descent (positive w) is found where Q vectors diverge and forcing for ascent (negative w) is found where Q vectors converge.
In this form the vertical motion is only a function of
the divergence of the vector Q
n this form the vertical motion is only a function of the divergence of the vector Q. This can be analyzed
on weather maps (by computers) to diagnose the omega field
In this form the vertical motion is only a function of the divergence of the vector Q. This can be analyzed on weather maps (by computers) to diagnose the omega field. The rule to remember is:
Divergence of Q means downward motion and convergence of Q means upward motion.
The advantage in using Q vector form of the QG Omega Equation is that
one can infer forcing for QG vertical motions without having to consider the “differential” aspect, as was required with the traditional form of the equation.
The advantage in using Q vector form of the QG Omega Equation is that one can infer forcing for QG vertical motions without having to consider the “differential” aspect, as was required with the traditional form of the equation.
We can simply
plot Q vectors and overlay computations of the Q-vector divergence to get an idea of where there is forcing for vertical motion.
concider a case used for evaluating Q
- Consider a hypothetical case of northerly and southerly low-level jets in the presence of a meridional temperature gradient as depicted
- Let the x axis be parallel to isentropes, with cold values to the north. Assume vg varies sinusoidally
- We will now evaluate Q at each of the points A–E indicated. Here, Q1 is the east–west component of the vector and Q2 is the north–south component.
- In this example, the only nonzero term is the second part of the Q1 vector
The resultant Q-vectors (represented by red arrows) indicate:
- Divergence of Q-vectors in the areas of cold advection, giving rise to descent
- • Convergence of Q-vectors in the areas of warm advection, giving rise to ascent
The red dots in figure indicate
zero-magnitude Q-vector.
Thus, regions of forcing for vertical motion in this example are exactly consistent with
what one would expect from the traditional form of the QG omega equation—local maxima of warm (cold) advection are associated with forcing for ascent (descent).
Quasi geostrophic theory can be used to form a conceptual model of how
an extratropical cyclone develops
Quasi geostrophic theory can be used to form a conceptual model of how an extratropical cyclone develops, through what is known as
Pettersons’s self development process
Quasi geostrophic theory can be used to form a conceptual model of how an extratropical cyclone develops, through what is known as Pettersons’s self development process
This occurs when
an upper-level trough approaches an old frontal boundary or baroclinic zone
This occurs when an upper-level trough approaches an old frontal boundary or baroclinic zone, due to
feedback between lower tropospheric thermal advection and upper wave
A
B
C
D
G
E
H
J
F
I
According to the figure
there will warm-air advection (WAA) in
and cold air advection (CAA) in
the southerly flow to the east of the surface cyclone
the northerly flow to the west of the surface cyclone.
As shown (Fig. a), there will warm-air advection (WAA) in the southerly flow to the east of the surface cyclone, and cold-air advection (CAA) in the northerly flow to the west of the surface cyclone.
This will
amplify the trough-ridge structure aloft (as shown by the dashed line in the figuer)
The amplified trough-ridge structure leads to
enhanced PVA over the surface low leads to an upward motion, more surface convergence, and a subsequent enhancement of the surface low.
The amplified trough-ridge structure leads to enhanced PVA over the surface low leads to an upward motion, more surface convergence, and a subsequent enhancement of the surface low.
The process continues to
repeat itself in a positive feedback loop
The amplified trough-ridge structure leads to enhanced PVA over the surface low leads to an upward motion, more surface convergence, and a subsequent enhancement of the surface low.
The process continues to repeat itself in a positive feedback loop.
The development process will proceed as long as
the upper-level trough is upstream of the surface cyclone, so that there is PVA over the surface cyclone.
