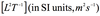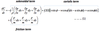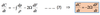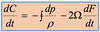Chapter 1 Flashcards
Circulation and vorticity are
the two primary measures of rotation in a fluid
Circulation is a
- scalar integral quantity
- macroscopic measure of rotation for a finite area of the fluid
Vorticity is a
- vector field
- microscopic measure of the rotation at any point in the fluid
draw an example of circulation and vorticity
What is the difference between macroscopic and microscopic
- Macroscopic:
- Large scale
- rotation of entire fluid –> circulation
- Microscopic:
- Very Small
- How individual particles rotate “any point within the fluid”
barotropic fluid
characterised by the absence of horizontal temperature gradients completely.
No horizontal gradient –> temperature is constant “Isotherm”
A barotropic fluid is one in which
the surfaces of constant pressure (p1, p2 …) and constant density (or specific volume) are parallel.
Specific volume (a):
volume of a unit mass of air
density (p):
mass/volume = 1/volume
specific volume = 1/p (when p constant volume is constant)
In a barotropic fluid, …………………..is a function of ………………and……………………………………………………
density
pressure only
density is constant along a constant pressure surface.
P1 stands for
Isotere (specific volume)
a1 stands for
Pressure uniform
ideal gas law:
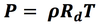
From ideal gas law:
If P is constant p is constant –> constant ratio = constant
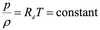
The law implies that
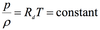
for a barotropic atmosphere, temperature is constant on a constant pressure surface.
for a barotropic atmosphere, temperature is constant on a constant pressure surface.
Therefore, in a barotropic fluid,
surfaces of constant pressure, constant density and constant temperature all are parallel.
Summary of barotropic fluid
No change in temperature and pressure –> no circulation due to these factors but circulation may develop due to other factors
baroclinic fluid
characterized by the presence of horizontal temperature variations.
A baroclinic fluid is characterized by the presence of horizontal temperature variations.
In such a fluid,
density is not a function of pressure alone and density variations occur due to horizontal temperature variations. Ex: Land and sea breeze.
Explain the figure
the isobars slope upwards towards the warm, while the isosteres slope upward over the cold.
Therefore, in a baroclinic fluid, the surfaces of constant pressure and constant specific volume intersect each other, forming quadrilaterals known as ‘solenoids’.
Fig. also shows that the solenoids give
rise to direct circulation (warm air rises and cold air sinks).
circulation is a
scalar quantity
Circulation
expresses the macroscopic rotational tendency of a finite area of a fluid.
The circulation, C, around a given closed curve in a fluid is
the integral around the curve of the components of the velocities along the curve
Circulation equation:
Draw a figure that better represent the circulation equation
Circulation has dimensions
If dx, dy, dz are components of ……, then
dl
- Circulation around a closed loop is, simply the integral of the tangential velocities around the loop.
- Hence, the mean tangential velocity <v> around</v>
the loop can be obtained from circulation (C) as follows:
where r is the radius of the circular loop
what are the terms in the following circulation theorem
What is the simplified version of the solenoidal term
Coriolis term
What is the simplified version of the circulation theorem
In a barotropic fluid, since density is a function of pressure only, we can write the solenoidal term as:
Therefore, for a barotropic fluid, the circulation theorem becomes:
Since in a baroclinic fluid, density is not a function of pressure alone, ____________Therefore, for a baroclinic fluid, the circulation theorem can be written as:
/o (a)(dp)not equal to 0
The observed circulation pattern is then solely due to the solenoidal effect and the circulation theorem can be written as:
A resembles
Circulation
B resembles
Vorticity
