Chapter 2 - Functions Flashcards
Where y = f(x), how is the inverse function written?
What is the reverse function?
x = f- -1(y)
In general, the inverse function of a function f is a function that reverses the operations carried out by f.
What graphical property does the functions f and f -1 have?
They are symmetrical about the line y = x.

What is a composite function?
A function of the form y = f(g(x)) is called a function of a function or a composite of the functions f(x) and g(x). In modern mathematical texts it is common to denote the composite function by f ° g.

What is an even function?
An even function is a function that satisfies the functional equation
f(-x) = f(x)
The graph of even functons is symmetrical about the y-axis.
Polynomial functions that only involve even powers of x are even functions. E.g. y = x4 + x2 - 2
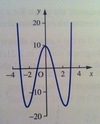
What is an odd function?
An odd function is a function that satisfies the functional equation
f(-x) = - f(x)
An odd function is antisymmetrical about the origin.
Polynomial functions that only involve odd powers of x are odd functions. E.g. y = x - x5
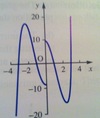
What is a periodic function?
A periodic function is such that its image values are repeated at regular intervalsin its domain. Thus the graph of a periodic function can be divided into “vertical strips” that are replicas of each other (picture).

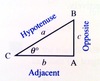
Given the triangle in the picture, how is the sine, cosine and tangent of the angle Ø given?

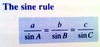
Why do we need the sine rule, and how is it defined?

We need the sine and cosine rules to work with triangles that are not right-angled.
Why do we need the cosine rule, and how is it defined?
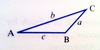
We need the sine and cosine rules when working with triangles that are not right-angled.

Given the picture, define the sine and cosine
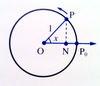
Sine is NP, and cosine is ON
Given the picture, how do you define the length of the arc?


Given the picture, how do you define the area of the sector?


Define sin x in terms of cosine, and cos x in terms of sine
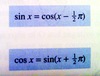
How are the secant, cosecant and cotangent functions defined?

cos2x + sin2x = ?
1 + tan2x = ?
1 + cot2x = ?

sin 2x can also be defined as___
cos 2x can also be defined as___
tan 2x can also be defined as___
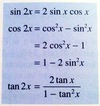
if y = ex, then x =
x = ln y
If ln ex = x, then eln y =
eln y = y


