Chapter 10 - Intro to Ordinary Differential Equations

Question 1

What is a differential equation?

Answer 1

A differential equation is an equation that involves not only algebraic combinatons of the variables occurring in the equation, but also derivatives of those variables with respect to other variables.

Question 2

In a differential equation, what are the dependent and the independent variables?

Answer 2

The dependent variables are the variables that are differentiated, while the independent variables are those which with respect to differentiation occurs.

In the picture, f is the dependent variable, while x and y are the independent variables.

Question 3

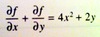
What is meant by “the order of a differential equation”?

Answer 3

The order of a differential equation is the degree of the highest derivative that occurs in the equation.

Question 4

How do you tell linear and nonlinear differential equations apart from one another?

Answer 4

Linear equations are equations in which the dependent variable or variables and their derivatives do not occur as products, raised to powers or in nonlinear functions,

Nonlinear equations are those that are not linear.

Question 5

What is the difference between homogeneous equations and nonhomogeneous equations?

Answer 5

In homogeneous equations, each term involves the dependent variable or one of its derivatives. In nonhomogeneous equations there is at least one term contains only the indepenent variable or a constant.

Question 6

What is meant by the general solution of a differential equation?

Answer 6

The general solution is the most general function that will satisfy the differential equation, and will normaly contain a number of arbitrary constants equal to the order of the differential equation.

Question 7

What is meant by the particular solution of a differential equation?

Answer 7

If you are supposed to find a particular solution of a differential equation, you are given values for the variables that you use to find the particular solution.
After finding the general solution, you implement the given values to find the value of the constants.

Question 8

What is the difference between analytical and numerical solutions to differential equations?

Answer 8

Differential equations have analytical solutions if they are solvable by the use of mathematical techniques. If a differential equation is unsolvable by the use of such mathematical techniques, the only way of solving the equation is by the use numerical techniques, leading to a numerical solution.

Question 9

Solve the differential equation:

18x dx + dy = 0

Answer 9

1. Separate x and y variables to different sides of the equation.

dy = - 18x dx

2. Integrate both sides.

y = - 9x² + C

Question 10

Solve the differential equation:

x²+(x³+12) y ‘ = 0

Answer 10

x²+(x³+12) dy/dx = 0

(x³+12)dy/dx = - x²

dy/dx = - x²/(x³+12)

dy = - 1 / (x³+12) * x²dx

Vi setter: u = x³+12

Det gir: du = 3x²dx

1/3 du = x²dx

Setter inn i ligningen:

dy = -1/3 * 1/u * du

Vi integerer begge sider, og får:

y = -1/3 * ln(x³+12) + C

Question 11

Solve the differential equation:

y ‘ + y = 3

Answer 11

dy/dx + y = 3

dy/dx + y - 3 = 0

dy + (y - 3)dx = 0

dy/(y - 3) = - dx

Integrating both sides, we get:

ln(y - 3) = - x + C

e^{ln(y - 3)} = e^{- x + C}

y - 3 = Ce^{- x}

y = Ce^{- x} + 3

Question 12

Find the particular solution of the given differential equation for the indicated values:

dy/dx + 5yx² = 0; x = 0 when y = 1

Answer 12

dy/dx + 5yx² = 0; y(0) = 1

dy/dx = - 5yx²

dy/y = - 5x²dx

Integrating both sides, we get:

ln y = - 5/3 x³ + C

We substitute the indicated values to find the constant C:

ln 1 = - 5/3 * 0 + C

C = 0

We now solve for y:

e^{ln y} = e^{- 5/3 x³}

y = e^{- 5/3 x³}

Question 13

Find the solution to the initial value problem:

dx/dt = 4sin(t)/x² , x(0) = 8

Answer 13

dx/dt = 4sin(t)/x² , x(0) = 8

x²dx = 4sin(t) dt

Integrating both sides, we get:

x³/3 = - 4cos(t) + C

Substituiting in the initial values, we have:

8³/3 = - 4cos(0) + C

C = 524/3

We now solve for x:

x³/3 = - 4cos(t) + 524/3

x³ = - 12 cos(t) + 524

x = (- 12 cos(t) + 524) ^1/3

Question 14

Find the solution of the initial value problem:

7t² dx/dt = 7/x , x(10) = 9

Answer 14

7t² dx/dt = 7/x , x(10) = 9

x dx = 7/7t² dt

= 1/t² dt = t^-2 dt

Integrating both sides, we get:

x²/2 = - 1/t + C

Substituting in initial values, we get:

9²/2 = - 1/10 + C

C = 203/5

Solving for x gives:

x²/2 = - 1/t + 203/5

x² = - 2/t + 406/5

x = (- 2/t + 406/5)^1/2

Question 15

Solve the differential equation:

4 (xy)^1/2 dy/dx = 1 , x, y > 0

Answer 15

4 (xy)^1/2 dy/dx = 1

4 x^1/2 y^1/2 dy/dx = 1

4 y^1/2 dy = x^{- 1/2} dx

Integrating both sides, we get:

8/3 y^3/2 = 2x^1/2

y^3/2 = 3/8 * 2x^1/2

y = (3/4 x^1/2) ^2/3

Question 16

Solve the differential equation:

dy/dx = 9e^{x - y}

Answer 16

dy/dx = 9 e^{x - y}

dy/dx = 9 e^x e^-y

1/e^{- y} dy = 9e^x dx

e^y dy = 9e^x dx

Integrating both sides, we get:

e^y = 9e^x + C

ln (e^y) = ln (9e^x) + C

ln (e^y) = ln 9 + ln (e^x) + C

Since ln 9 is a constant, we can let C₁ = ln 9 + C:

ln (e^y) = ln (e^x) + C

y = x + C

Question 17

Find the function y(x) satisfying

d²y/dx² = 14 - 30x,

y ‘ (0) = 7 and y(0) = 4

Answer 17

d²y/dx² = 14 - 30x

y ‘ (0) = 7 and y(0) = 4

d²y = (14 - 30x) dx²

Integrating both sides, we get:

dy = y’ = 14x - 15x² + C₁

y ‘ (0) = 7 = C₁

C₁ = 7

We now have:

dy = 14x - 15x² + 7

Integrating both sides again, we get:

y = 7x² - 5x³ + 7x + C₂

y(0) = 4 = C₂

C₂ = 4

Finally, we have:

y = 7x² - 5x³ + 7x + 4

Question 18

Okei, vi sier det er greit å bytte mellom norsk og engelsk…!

Hva er den karakteristiske ligningen til differensiallikningen

y ‘ ‘ + y ‘ - 2y = 0

?

Answer 18

Den karakteristiske ligningen “gjør om” på differensialligningen, slik at deriverte blir til potenser:

Differensialligningen

y ‘ ‘ + y ‘ - 2y = 0

har den karakteristiske ligningen

r² + r - 2 = 0

Question 19

En karakateristisk ligning med nullpunktene 3 og - 2 har den generelle differensialløsningen y(x) = _____

Answer 19

y(x) = Ce^3x + De^-2x

Question 20

Hvis den karakteristiske ligningen har to forskjellige reelle røtter, r₁ og r₂, hva er den generelle løsningen av differensialligningen?

Answer 20

y(x) = Ce^r₁x + De^r₂x

Question 21

Hvis den karakteristiske ligningen har reell dobbelrot r, hva er den generelle løsningen av differensialligningen?

Answer 21

y(x) = Ce^rx + Dxe^rx

Question 22

Hvis den karakteristiske ligningen har to forskjellige komplekse røtter r₁ og r₂ som er slik at r₁ = a + ib og r₂ = a - ib

hva er den generelle løsningen av differensialligningen?

Answer 22

y(x) = e^ax(C cos(bx) + D sin(bx))

Question 23

Gitt den inhomogene differensialligningen, finn én løsning.

y ‘ ‘ + 5y ‘ - 9y = x²

Answer 23

y ‘ ‘ + 5y ‘ - 9y = x²

Vi prøver med y = Ax² + Bx + C

y ‘ = 2Ax + B

y ‘ ‘ = 2A

Setter vi inn i ligningen får vi:

2A + 5(2Ax + B) - 9(Ax² + Bx + C) = x²

2A + 10Ax + 5B - 9Ax² - 9Bx - 9C = x²

Hvis vi tenker at det på høyre side står:

= x² + 0x + 0

og sammenligner ledd av samme orden hver for seg, får vi:

-9A = 1 (-9Ax² = 1x²)

A = - 1/9

10A - 9B = 0

9B = 10A –> B = 10/9 * A –> B = - 10/81

2A + 5B - 9C = 0

9C = - 2/9 - 50/81 = - 68/81

C = - 68/729

Vi bytter nå inn verdiene for A, B og C:

y = - 1/9 * x² - 10/81 * x - 68/729

Question 24

La y₁ og y₂ være løsninger av en inhomogen differensialligning y. Hva er y₁ - y₂ da?

Answer 24

y₁ - y₂ er da den generelle løsningen for den tilsvarende homogene differensialligningen til y

Question 25

Hvordan finner vi den generelle løsningen til en inhomogen differensialligning?

Answer 25

1. Finn den generelle løsningen av den tilsvarende homogene differensialligningen.
2. Finn en partikulærløsning av den inhomogene differensialligningen.
3. Den generelle av den inhomogene differensialligningen er summen av disse to løsningene.

y = y_p + y_h

Question 26

Gitt den homogene tredjeordens differensialligningen

9y ‘ ‘ ‘ - 9y ‘ ‘ - 4y ‘ + 4y = 0

Hvordan finner man den generelle løsningen?

Answer 26

1. Skriv først den karakteristiske ligningen:

9r³ - 9r² - 4r + 4 = 0

2. Finn nullpunktene til den karakteristiske ligningen. Siden ligningen inneholder et konstantledd, må man her ofte gjette/finne det første nullpunktet på egen hånd, før deretter å finne de resterende 2 ved polynomdivisjon.

r₁ = 1

r₂ = 2/3

r₃ = - 2/3

3. Siden den karakteristiske ligningen har 3 forskjellige reelle røtter (i motsetning til trippelrot og komplekse røtter), har den generelle løsningen formen:

y(x) = Ae^x + Be^{2/3 * x} + Ce^{- 2/3 * x}

Question 27

Finn den generelle løsningen til den inhomogene differensialligningen:

y ‘ ‘ - 3y ‘ + 4y = cos(4t) - 2sin(4t)

Answer 27

Vi vet at y = y_h + y_p

1. Finner den generelle løsningen til den tilsvarende homogene ligningen.

y ‘ ‘ - 3y ‘ + 4y = 0

1.a. Finner nullpunktene til den karakteristiske ligningen.

r² - 3r + 4 = 0

r = 3/2 +- i(7^1/2/2)

1.b. Den generelle løsningen til den homogene ligningen er da:

y_h = e^{3/2 t} [C cos(7^1/2/2 t) + D sin(7^1/2/2 t)]

2. Finner en partikulær løsning for den inhomogene ligningen. Vi leser høyresiden av ligningen, og prøver oss med:

y_p = E cos(4t) + F sin(4t)

y_p ‘ = - 4E sin(4t) + 4F cos(4t)

y_p ‘ ‘ = - 16E cos(4t) - 16F sin(4t)

2. a. Vi setter disse verdiene inn i den originale ligningen.
   - 16E cos(4t) - 16F sin(4t) + 12E sin(4t) - 12F cos(4t) + 4E cos(4t) + 4F cos(4t) = cos(4t) - 2 sin(4t)
3. b. Vi trekker sammen koeffisientene som står forran cosinus på venstre side av ligningen, og setter dette lik koeffisienten forran cosinus på høyre side.
   - 12E - 12F = 1
4. c. Vi gjør det samme for sinus.

12E - 12F = - 2

2. d. Vi summerer disse ligningene, og får:
   - 12E + 12E - 12F - 12F = 1 - 2
   - 24F = -1
3. e. Vi løser for F og E

F = 1/24

E = - 1/8

2.f. Den partikulære løsningen til den inhomogene ligningen er da

y_p = - 1/8 cos(4t) + 1/24 sin(4t)

3. Vi trekker nå sammen y_h og y_p for å finne løsningen.

y = y_h + y_p =

e^{3/2 t} [C cos(7^1/2/2 t) + D sin(7^1/2/2 t)] - 1/8 cos(4t) + 1/24 sin(4t)

THE END