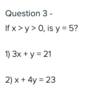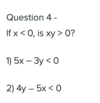6 - Inequalities and Absolute Values

Question 1

What do you do when multiplying or dividing a compound inequality by a negative number?

Answer 1

Flip the sign

Question 2

What do you do when multiplying or dividing an inequality by a negative number?

Answer 2

Flip the sign

Question 3

What is the rule for adding inequalities?

Answer 3

The sign must be facing the same direction.

Question 4

What is true about x + y?

x < 26

8 > y

Answer 4

What is true about x + y?

x < 26

8 > y

Flip the inequality to make the signs face the same direction.

x < 26

y < 8

Add.

x + y < 34

Question 5

When can you multiply or divide a compound inequality by a variable?

Answer 5

Only when the sign is known.

Question 6

What must be done when manipulating a compound inequality?

Answer 6

Every part of the inequality must be changed the same way:

-4 < x < 5

If multiplying -4 by 3, all parts must be multiplied by 3.

3(-4 < x < 5)

=> -12 < 3x < 15

Question 7

Substitution example: equation and inequality

Answer 7

Question 8

When comparing multiple inequalities, you should use what tool?

Answer 8

The number line.

Question 9

x² < 81

What is x?

Answer 9

x < 9

x > -9

-9 < x < 9

Question 10

If -80 < a < 10 and -20 < b < 15, what is the maximum possible value of ab minus the minimum possible value of ab?

Answer 10

• 80 * -20 = 1600 = maximum value of ab
• 80 * 15 = -1200 = minimum value of ab
  (1600) - (-1200)= 2,800

Question 11

Inequalities with absolute value signs be solved…

Answer 11

twice. Once with the value inside the absolute value bars as positive and once as negative.

Question 12

If |x| + 6 = 10, what is the value of x?

Answer 12

If |x| + 6 = 10, what is the value of x?

Solve once as if what’s in the absolute value bars is positive. NOTE the absolute value sign must be isolated to one sign of the equation by itself first.

|x| + 6 = 10

|x| = 4

x = 4

Solve once as if what’s in the absolute value bars is negative.

x| + 6 = 10

|x| = 4

-x = 4

x = -4

Both 4 and -4 are possible values for x. NOTE THAT IT WILL NOT ALWAYS EQUAL THE OPPOSITE SIGN.

-

Question 13

Create a compound inequality from |x| < b

Answer 13

-b < x < b

Question 14

What must be done before solving an absolute value equation?

Answer 14

Isolate the absolute value to one side by itself.

Question 15

300 |x² + x - 9| = 900, then what is the sum of all possible values of x?

Answer 15

Question 16

If two absolute values are equal, what must be true about the expressions in the absolute value bars?

Answer 16

They must be either equal or opposite.

|5| = |5|

OR

|5| = |-5|

Question 17

What is the correct inequality sign to replace the symbol?

|a - b| @ |a| - |b|

Answer 17

|a - b| > |a| - |b|

Question 18

What is the correct inequality sign to replace the symbol?

|a + b| @ |a| + |b|

Answer 18

|a +b| < |a| + |b|

Question 19

Solve for x

|x| > 20

Answer 19

Question 20

|x +1| = -2

Answer 20

No solution because the absolute value cannot be equal to a negative value.

Question 21

Answer 21

Question 22

Answer 22

Question 23

Answer 23

Question 24

Answer 24

Question 25

Answer 25

Question 26

Answer 26

Question 27

Answer 27

Question 28

Answer 28

Question 30

Answer 30

Question 31

Answer 31

Question 32

Answer 32

Question 33

Answer 33

Question 34

Answer 34