Brainscape's Knowledge GenomeTM

Browse over 1 million classes created by top students, professors, publishers, and experts.


See full index

GMAT > 11 - Ratios > Flashcards

11 - Ratios Flashcards

1
Q

Find the ratio of a:c given A=2B and B=3C

A

Find the ratio of a:c given a=2b and b=3c

a/2=b => a/2=3c => a = 6c => a/c= 6

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
2
Q

Ratio

A

Comparison between two or more quantities or magnitudes, how parts of a whole relate to each other and how those parts relate to the whole.

If there are 5 men in a room and 10 women, ratio is 5:10, reduced to 1:2 using the gcf of 5 to divide both.

Expressions:

5:10

5 to 10

5/10

These numbers can be flipped by changing the language (e.g., “the number of women to men” would make it 10:5.)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
3
Q

Ratio multiplier

A

The ratio of men to women is 1:2. If you know the multiplier, you can get the total number.

Men:Woman 1:2

multiplier = 5

1(5):2(5)

You can also use it to set up an equation.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
4
Q

X is inversely propotional to the cube of y and directly proportional to the square root of z

A

x = k * radical(z)/y3

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
5
Q

x is inversely jointly proportional to the square of B and the 4th root of c.

A

k

(b2 * ∜c)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
6
Q

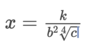
The volume of a cylinder is jointly proportional to the height, h, and square of the base’s radius, r.

A

V= k * hr2

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
7
Q

Ratio of apples to pears = 5:3. If there are 45 apples, how many need to be removed to make the ratio 2:3?

A

Ratio of apples to pears = 5:3. If there are 45 apples, how many need to be removed to make the ratio 2:3?

There ratio multiple is 9(5:3) = 45:27.

Subtract variable from what’s being reduced and then cross-multiply to remove denominators:

(45-y)/(27)=2/3

18/27=2/3

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
8
Q

Adjusting ratios with multiplication and division: sugar, vanilla, eggs in a 12:6:3 ratio. Halve the sugar to vanilla and triple the sugar to eggs. Final contas 4 oz of sugar, what is the total oz of the dessert?

A

Adjusting ratios with multiplication and division: sugar, vanilla, eggs in a 12:6:3 ratio. Halve the sugar to vanilla and triple the sugar to eggs. Final contas 4 oz of sugar, what is the total oz of the dessert?

original sugar:vanilla is 12:6, halve the sugar: 6:6

original sugar:eggs is 12:3, triple the sugar: 36:3->12:1

12:12:1

12x = 4oz => x=1/3 => 4:4:1/3 = 8+1/3oz

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
9
Q

Proportions

The density of an object is the ratio of its mass to its volume. A certain piece of metal with a mass of 1,200 grams has a density of 100 units. What would be the density of a similar piece of metal with the same volume and a mass of 3,600 grams?

A

Proportions

The density of an object is the ratio of its mass to its volume. A certain piece of metal with a mass of 1,200 grams has a density of 100 units. What would be the density of a similar piece of metal with the same volume and a mass of 3,600 grams?

1,200 grams/100units = 3,600 grams/x units

Cross multiply to get:

x = 300

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
10
Q

Proportion: Direct Variation Equation

A

When the ratio between two variables is a constant, they are related by the equation y = kx, where k is the positive constant. When x increases, y increases, when x decreases, y decreases.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
11
Q

A car with mileage of 60mpg uses one-half gallon every 15 miles, how many gallons @ 40mph for 40 miles?

A

A car going 60mph uses one-half gallon every 15 miles, how many gallons @ 40mph for 40 miles?

=> one-half gallon every 15 miles = 30mpg => 60=30k => k=2

=> 40=kx => 40 = 20 * 2 => 20mpg going 40 miles = 2 gallons.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
12
Q

Inverse variation (x, y)

A

x increases, y decreases

x decreases, y increases

y=k/x or xy=k

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
13
Q

Multipart ratio and LCM

Ratio 1

x:y = 3:4

Ratio 2

x:2 = 7:11

A

Multipart ratio and LCM

Ratio 1

x:y = 3:4

Ratio 2

x:2 = 7:11

  1. Find LCM of common variable x (7,3) = 21
  2. Multiply ratio one by 7 7(3:4)= 21:28
  3. Multiply ration two by 3 3(7:11) = 21:33
  4. x:y:z = 21:28:33
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
14
Q

Practice language variations on inverse and direct relationships

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
15
Q

Language Variations on inverse and direct relationships

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
16
Q
A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
17
Q

A collegiate athletic coach ordered an equal number of medium and large T-shirts for her team. However, 8 extra medium T-shirts were delivered, making the ratio of miedium to large T-shirts 5:3. What is the ratio of the total number of T-shirts that teh coach originally ordered to the number of medium T-shirts that were actually sent to her?

A

A collegiate athletic coach ordered an equal number of medium and large T-shirts for her team. However, 8 extra medium T-shirts were delivered, making the ratio of miedium to large T-shirts 5:3. What is the ratio of the total number of T-shirts that teh coach originally ordered to the number of medium T-shirts that were actually sent to her?

Write an equation equal to the new ratio.

medium/large = x+8/x=5/3.

Cross-multiply.

3(x + 8) = 5x

=> 3x + 24 = 5x

=> 24 = 2x

=> x = 12

Original order was 12 medium shirts + 12 large shirts. 12 + 8 = 20 medium shirts were sent.

24/20 = 6/5 = 6 : 5 = original t-shirts ordered : number of mediums sent.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
18
Q

A baking reciper calls for sugar, flower and milk, and no other ingredients, to be mixed together in a ratio of 2:3:7. if 5 cups of flower are available, how many cups of the recipe can be made?

Find the ratio multiplier from the ratio 2x:3x:7x

3x = 5

=> x = 5/3

Add total total from ratio.

2x + 3x + 5x = 12x.

Multiply by the ratio multiplier.

=> 12x(5/3) = 60/3 = 20 cups

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
19
Q

In town A, the population is comprised entirely of Republicans and Democrats. The ratio of Republicans to Democrats is 13:2. Had 50 new Republicans and 120 new Democrats moved to town A, the ratio of Republicans to Democrats would then be 3 to 2. What is the current number of Republicans in Town A?

A

In town A, the population is comprised entirely of Republicans and Democrats. The ratio of Republicans to Democrats is 13:2. Had 50 new Republicans and 120 new Democrats moved to town A, the ratio of Republicans to Democrats would then be 3 to 2. What is the current number of Republicans in Town A?

Use the old ratio to set up an equation equal to the new ratio to find the ratio multiplier.

13x+50 / 2x + 120 = 3/2.

Cross-multiply.

2(13x + 50) = 3(2x + 120)

26x + 100 = 6x + 360

20x = 260

x = 13

Use the ratio multiplier (x = 13)to find the current number of Republicans.

13(13) = 169 current Republicans

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
20
Q

A survey of high school students found that 1/2 of the female students searched the Internet and 2/3 of the male students searched the Internet. Furthermore, the survey found that 1/4 of the female students searched the Internet from coffee shops and 1/6 of the male students also searched the Internet from coffee shops. If equal numberss of male and female students were surveyed, then what fraction of the students who search the internet do so from coffee shops?

A

A survey of high school students found that 1/2 of the female students searched the Internet and 2/3 of the male students searched the Internet. Furthermore, the survey found that 1/4 of the female students searched the Internet from coffee shops and 1/6 of the male students also searched the Internet from coffee shops. If equal numbers of male and female students were surveyed, then what fraction of the students who search the internet do so from coffee shops?

Add ratios together for the numerator (number of students who search internet from a coffee shop) and the denominator (the total number of students who search internet). Use x to represent the number of students (male and female = equal number so only x is needed). Multiply by lcd 12 to get rid of the complex fractions fractions.

12(1/4x + 1/6x) / 12(1/2x + 2/3x)

=> 3x + 2x / 6x + 8x

=> 5x / 14x

=> 5/14

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
21
Q

Ratio Multiplier Baking Question

A

Must find the common numerator of the common variable, Flour.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
22
Q
A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
23
Q

When setting equations equal to variables

A

Cross-multiply to make the equation faster to solve

24
Q

Johnny collects baseball cards and football cards. In his current collection, the ratio of baseball cards to football cards is 5 to 3. If the total number of baseball cards in his collection is 300, how many baseball cards would Johnny have to get rid of to make the ratio of baseball cards to football cards 1:2?

A

Johnny collects baseball cards and football cards. In his current collection, the ratio of baseball cards to football cards is 5 to 3. If the total number of baseball cards in his collection is 300, how many baseball cards would Johnny have to get rid of to make the ratio of baseball cards to football cards 1:2?

Get the ratio multiplier to find the second value.

5x = 300

x= 60

3x = 18

Set equation of 300 cards - x / 180 equal to new ratio.

300 - x / 180 = 1/2

Cross-multiply.

2(300 - x) = 1(180)

600 - 2x = 180

2x = 420

x = 210 cards need to be removed

25
Q

Using fractions to solve ratio question

A
26
Q

In a certain business school, there are 10 times as many students over 25 years old as there are students under 25 years old. If no students are exactly. 25 years old, what is the ratio of the number of students under 25 to the total number of students at the business school?

A

In a certain business school, there are 10 times as many students over 25 years old as there are students under 25 years old. If no students are exxactly. 25 years old, what is the ratio of the number of students under 25 to the total number of students at the business school?

1 to 11

Remember the denominator is the total number of business school students.

27
Q

Ratios with 3 unknown variables

A
28
Q
A
29
Q

PLACEHOLDER

A
30
Q

PLACEHOLDER

A
31
Q

PLACEHOLDER

A
32
Q
A
33
Q
A
34
Q
A
35
Q
A
36
Q
A
37
Q
A
38
Q
A
39
Q
A
40
Q
A
41
Q
A
42
Q
A
43
Q
A
44
Q
A
45
Q
A
46
Q
A
47
Q
A
48
Q
A
49
Q
A
50
Q
A
51
Q
A
52
Q
A
53
Q
A
54
Q
A
55
Q
A
56
Q
A

GMAT (19 decks)

Brainscape helps you reach your goals faster, through stronger study habits.
© 2024 Bold Learning Solutions. Terms and Conditions