4 - Number Properties Flashcards
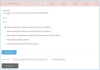
odd + odd =
even
even + even =
even
even + odd =
odd
odd - odd =
even
even - even =
even
even * even =
even
even * odd =
even
odd * odd =
odd
even/odd
even
odd/odd =
odd
even/even =
even or odd
Prime Numbers 0-9
2, 3, 5, 7
Prime Numbers 10-19
11, 13, 17, 19
Prime number 20-29
23, 29
Prime Numbers 30-39
31, 37
Prime Numbers 40-49
41, 43, 47
Prime Numbers 50-59
53, 59
Prime Numbers 60-69
61, 67
Prime Numbers 70-79
71, 73, 79
Prime Numbers 80-89
83, 89
Prime Numbers 90-99
97
Factors
If y divides evenly into x, we say y is a factor of x. 25 divides evenly into 100 so it is a factor of 100.
Multiple
Product of that number and any integer
Formula for division
x/y = quotient + remainder
Divisibility by 2
ones digit is 0, 2, 4, 6, 8
Divisibility by 3
sum of all the digits = a number that is divisible by 3
Divisibility by 4
last two digits are divisible by 4
Divisibility by 5
last digit is 5 or 0
Divisibility by 6
divisible by 2 and 3
Divisibility by 8
last three digits = a number divisible by 8, also 000
Divisibility by 9
sum of all the digits = a number divisible by 9
Divisibility by 11
(sum of the odd-numbered place digits) - (the sum of the even-numbered place digits)
is divisible by 11
Range of possible remainders
Remainder must be a non-negative integer that is less than the divisor
Finding the number of factors in a particular number
- Find the prime factorization
- Add 1 to each exponent
- Multiply the exponents
Finding LCM
- Prime factorize each integer and put them in exponent form
- For any repeated #’s, take only the one with the largest exponent
- Multiply
Finding GCF
- Prime factorize each number and write in exponent form
- Take only the numbers common to all, and the lowest exponent
- Multiply
LCM * GCF
If the LCM of x and y is p and the GCF of x and y is q, then xy=pq
So if you multiply the LCM and GCF of a pair, it will be equal to multiplying the pair together.
Units digit for factorials greater than or equal to n! will always have zero as the units digit
Units digit for factorials greater than or equal to 5! will always have zero as the units digit
Number of trailing zeroes in a number =
number of (5x2) pairs
Leading Zeroes
If X is an integer with k digits, then 1/x will have k-1 leading zeroes unless x is a perfect power of 10, in which case there will be k-2 trailing zeroes
Terminating Decimals
The decimal equivalent of a fraction will terminate if and only if the denominator of the reduced fraction has a prime factorization that contains only 2s or 5s or both.
Units Digits for 0
0
Units Digits for 2
2-4-8-6
Units Digits for 3
3-9-7-1
Units Digits for 4
4-6: odd powers end in 4, even powers end in 6
Units Digits for 5
5
Units Digits for 6
6
Units Digits for 7
7-9-3-1
Units Digits for 8
8-4-2-6
Units Digits for 9
9-1. Odd, positive powers end in 9 and even, positive powers end in 1.
Perfect squares
All of its prime factors have even exponents
Perfect Cubes
Prime factors have exponents divisible by 3
GCF of two consecutive integers
1 because they will never share any prime factors.
Remainder Theory
19/7= 2+5/7
19=dividend
7= divisor
2= quotient
5= remainder
x/y= q+4/y
x=qy+r
q=(x-r)/y
r=x-qy
Determine number of trailing zeroes in a factorial
200!
200!/5 = 40
200!/(52)=8
200!/53=1
200!/54=0
=49 5’s in the number so there are 49 0’s. Always divide by 5.
Even and Odd numbers
- all even numbers have an even units digit
- all odd numbers have an odd units digit
- even integers can be represented by 2n
- odd numbers can be represented either by 2n+1 or 2n-1
Factorial Facts and Division Properties
4! = 4*3*2*1
1! = 1
0! = 1
integers are consecutive
divisible by any of the integers in the factorial and by any combo of those factors
Using trailing zeroes to find total number of digits
- Prime factorize
- Count the number of (5*2) pairs, each contributes one trailing zero
- Multiply the remaining numbers and count the digits of the product
- Total = sum of #2 and #3
What is the greatest value of positive integer x such that 2x is a factor of 10080?
What is the greatest value of positive integer x such that 2x is a factor of 10080?
(22*52)80
=> 2160, so 160 is the greatest possible value of x
Determining number of primes in a factorial when the divsor is not prime: What is the largest integer value of n such that 40!/6n is an integer?
- Break divisor into primes
- Use shortcut with the largest prime
40!/6n
40!/(2*3)n
3 is the largest prime.
40/3 = 13
40/32 = 4
40/33 = 1
40/34 = 0
Largest value for n is 13+4+1=18.
Remainders after division by 10
Remainder = units digit for 1/10, last two digits for 1/100, last three digits for 1/1000
93/10 = 9+3/10
993/100 = 9+93/100
9993/1000=9+993/1000
First non-negative multiple of any integer
0
Absolute Value
Distance from 0 on the number line.
| 7 | = 7
-7 | = 7
Remainder patterns
Remainder patterns repeat infinitely and can be found using small numbers.
If n is a positive integer and the product of all integers from 1 to n, inclusive, is a multiple of 990, what is the least possible value of n?
A. 10
B. 11
C. 12
D. 13
E. 14
If n is a positive integer and the product of all integers from 1 to n, inclusive, is a multiple of 990, what is the least possible value of n?
Factor 990: 213251111
It must have an 11 so the answer is b.
Rules of 0
- 0 multiplied by any number is 0.
- 0 divided by any number (except 0) is 0.
- A number divided by 0 is undefined.
- radical(0) = 0
- 0 raised to any positive power is 0.
- 0 is the only number this is neither positive nor negative.
- 0 is the only number that is equal to its opposite (-0).
- 0 is a multiple of all numbers.
- 0 is the only number that is equal to all its multiples.
- 0 is not a factor of any number except 0.
- Any non-zero number raised to 0=1.
- 0 is an even number.
- 0 can be added or subtracted to any number without changing the value of that number.
- 0!=1
If (30!*30!)/30n is an integer, what is the largest possible value of integer n?
A. 12
B. 13
C. 14
D. 15
E. 16
If (30!*30!)/30n is an integer, what is the largest possible value of integer n?
A. 12
B. 13
C. 14
D. 15
E. 16
=> 30 = (3*5*2). Take the largest prime, 5 and divide from the first 30.
30/5 = 6, 30/52=1, 30/53=0
7 * 2 (for the second 30!) = 14
When a certain number x is divided by 63, the remainder is 27. What is the remainder when x is divided by 7?
When a certain number x is divided by 63, the remainder is 27. What is the remainder when x is divided by 7?
x/63=q+27/63
x=63q + 27
x=(9 * 7)q +27
The first term is divisible by 7 so we only need to know 27/7 = 3 + R6.
Factoring out a factorial
(11!*10!* + 10!9!)/111
What is the greatest prime factor?
Factoring out a factorial
(11!*10!* + 10!9!)/111
What is the greatest prime factor?
10!(11! + 9!)/111
9!10!(11*10 + 1)/111
9!10!(111)/111
111 cancels from the numerator and denominator so the greatest prime factor is 7?
Shortcut for determining the number of a primes in a facotrial when the base is not prime (and breaks into only 2’s): What is the largest integer value of n such that 30!/4n is an integer?
Shortcut for determining the number of a primes in a facotrial when the base is not prime (and breaks into only 2’s): What is the largest integer value of n such that 30!/4n is an integer?
30!/(2)2n
30/2 = 15, 30/22 = 7, 30/23 = 3, 30/24 = 1, 30/25 = 0
15+7+3+1=2n
26/2=n
n less than or equal to 13
Original price=w, new price= 16%w
Which could be the original price?
A. 27
B. 28
C. 29
D. 31
E. 32
Original price=w, new price= 16%w
Which could be the original price?
A. 27
B. 28
C. 29
D. 31
E. 32
W*16/100=n
W*4/25=n
Must be a multiple of 4 so the answer is 28.
Evenly spaced sets
numbers increase by the same amount (common difference - arithmethic sequence)
Convert decimal to a remainder if you have?
The divisor. 9/5=1.8 (.8*5=4). Remainder is 4.
What can LCM tell us about a set of positive integers?
- All unique prime factors by factoring the LCM
- note: multiplying the numbers in a given set does not produce any additional unique prime factors
Factors of factors
if x/y is an integer then x/any factor of y is an integer.
24/6=4
24/(3*2)=4
thus
24/3=8
24/2 =12
are integers.
If x and y are positive integers such that x>y>1 and 2=x/y, which of the following must be true?
I. z > x-1/y-1
II. z< x-1/y-1
III. z>x+1/y+1
If x and y are positive integers such that x>y>1 and 2=x/y, which of the following must be true?
I. z > x-1/y-1
II. z< x-1/y-1
Subtracting a positive constant from a fraction greater than one will make it larger.
III. z>x+1/y+1
Adding a positive constant to a fraction greater than one will make it smaller.
Estimation and manipulating exponents and scientific notation
2007/20*2003
Express in form 20x * 10y
Estimation and manipulating exponents and scientific notation
2007/20*2003
cancel out 2007/2003 = 2004
2004/20 = (204 * 104)/201 = (203 * 104)/1 = 203 * 104
cancel out the 20 in the denominator
Product of N consecutive integers is divisible by?
N!
3x4x5=60
60/3!=10
Where 3 is the number of terms in the set of consecutive integers
Properties of One
- One is a factor of all numbers, and all numbers are multiples of one
- One raised to any power is one
- Multiplying or diving any number by one will not change the number
- One is an odd number
- One is the only number with exactly one factor
- One is not a prime number (the first prime number is 2)
xpositive integer does what to the unique prime factors?
nothing
Two unique or distinct prime factors
Not equal to each other (cannot be 52, for example)
LCM can solve repeating pattern questions
If blinking light L flashes every 12 seconds and blinking light M flashes every 32 seconds, and they both flash together at 8am, when will they flash at the same time again?
LCM(12,30) = 96 seconds later
If x and y are positive integers, is xy/6 an integer?
I. 48xy/6 is an integer
II. 49xy/6 is an integer
If x and y are positive integers, is xy/6 an integer?
I. 48xy/6 is an integer
II. 49xy/6 is an integer
=> II. Alone is sufficient becuase 49 is not divisible by 6 so xy must be divisible by 6.
Algebraic expressions of consecutive integers
- n(n+1)
- n(n-1)
- (n+3)(n+4)
Product of consecutive odd integers and consecutive even integers
- (n+1)(n-1)
- If n is an odd integer, (n+1) and (n-1) must be even. (n+1)(n-1) will be the product of the two consecutive even integers.
- If n is an even integer, (n+1) and (n-1) must be odd. (n+1)(n-1) will be the product of the two consecutive odd integers.
Multiplication of Remainders
(12 * 13 * 17)/5
- Use the divisor to find the remainder of each number
- Multiply the remainders
- If the product is larger than the divisor, subtract the divisor from it enough until it’s less than the divisor
- The result is the true remainder
12/5 = 2 + 2/5 = 2
13/5 = 2 + 3/5 = 3
17/5 = 3 + 2/5 = 2
2*3*2 = 12
12-5-5 = 2
Remainder of (12 * 13 * 17)/5 is 2.
Adding and Subtracting Remainders of Large Numbers
If n is an integer and (9! + 8! + 7!)/3n is an integer, what is the highest possible value of n?
If n is an integer and (9! + 8! + 7!)/3n is an integer, what is the highest possible value of n?
=> 7! (9x8 + 8 + 1)
=> 7!(81) => (7*(3*2)*5*4*3*2*1)(34)
Multiply the 3’s = 36
6 is the highest value of n.
If n is a positive integer and r is the remainder when n3 - n is divided by 9, what is the value of r?
I. n has a remainder of 1 when it is divided by 9
II. n2 has a remainder of 1 when it is divided by 9
If n is a positive integer and r is the remainder when n3 - n is divided by 9, what is the value of r?
I. n has a remainder of 1 when it is divided by 9
=> n3-n = n(n+1)(n-1) => n/9 = k + 1 => n = 9k + 1
=> n3-n = 9k+1(9k+1+1)(9k-1)
n has a multiple of 9 and therefore r=0.
Statement I is sufficient.
II. n2 has a remainder of 1 when it is divided by 9
n2 = 9k + 1
n3-n = n(n2 - 1)
n3-n = n(9k)
n has a multiple of 9 and therefore r=0.
Statement II is sufficient.
What is the greatest prime factor of 212 - 1?
What is the greatest prime factor of 212 - 1?
It is a difference of squares.
=> (26 + 1)(26 - 1) => (65)(63) = (13 * 5)(32 * 7)
The greatest prime factor is 13.
The variables m and n are positive integers. When n is divided by 18, there is a remainder of 12. When n is divided by 24, there is a remainder of 14. Which of the following are possible values of (m+n)?
I. 50
II. 70
III. 92
The variables m and n are positive integers. When m is divided by 18, there is a remainder of 12. When n is divided by 24, there is a remainder of 14. Which of the following are possible values of (m+n)?
I. 50
II. 70
III. 92
=> m/18 = q + 12/18 => m = 18q + 12
=> n/24 = a + 14/24 => n = 24a + 14
=> m + n = 18q + 12 + 24a + 14 => m + n = 18q + 24a + 26
Use fundamental rule of remainders by choosing a number that divides evenly into 18 and 24 and leaves a remainder for 26. In this case, 6 works.
=> 18q/6 + 24a/6 + 26/6
=> remainder = 2
Divide answer choices by 6 to see where you get a remainder of 2 and those are your answers.
=> 50/6 = r2, 70/6 = r4, 92/6 = r2
=> Answer: I and III
If n is a two-digit integer, how many different values of n allow n3 - n to be a multiple of 12?
If n is a two-digit integer, how many different values of n allow n3 - n to be a multiple of 12?
9 < n < 99
Multiples of 12 are divisible by 3 and 4
n3 - n = n(n+1)(n-1)
These are three consecutive integers so n3 - n is divisible by 3! so focus on 4 only.
If n is odd, n3 - n produces two even numbers (each a multiple of 2, 2*2=4).
(99 - 10) + 1= 90/2 = 45 instances.
If n is even, n3 - n produces only one even number that will be a multiple of 4. # of 2-digit multiples of 4 is (highest multiple - lowest multiple)/multiple + 1.
(96 - 12)/4 + 1 = 22 instances.
Answer = 67
If q = 40! +1 , which of the following cannot be a prime factor of q?
I. 11
II. 19
III. 37
If q = 40! +1 , which of the following cannot be a prime factor of q?
I. 11
II. 19
III. 37
All three because consecutive numbers cannot share the same prime factors.
If k is a positive integer 0 < x < 1,000, is (128/radical(x2)) an integer?
I. x = k6
II. k = 2y, where y is a positive integer
If k is a positive integer and 0 < x < 1,000, is (128/radical(x2)) an integer?
I. x = k6
k = 16 = 1 OR k = 26 = 64 OR k = 36 =729. Not sufficient.
II. k = 2y, where y is a positive integer
This means k is an even number. Not sufficient.
Both I & II.
k is even so x must be 64, so the question can be answered. Sufficient.
If integers ending in 0 are excluded, what is the units digit of the product of the even integers from 202-298?
If integers ending in 0 are excluded, what is the units digit of the product of the even integers from 202-298?
Multiply units digits in the first set of ten to get the pattern and then raise it to the power of ten.
2*4*6*8 = 38410
Units digits for 4 are 4-6 where 6 is the units digit for even powers.
The units digit is 6.
Edge Question


Properties of n3 - n
n3 - n
n(n+1)(n-1)
- Difference of squares.
- Represents three consecutive integers so it is divisible by 3!
- If n is odd then (n-1) and (n+1) will be even and the expression will be divisible by 2, 3, 4, 6 and 8. It’s divisible by 8 because one even number is a multiple of 2 and one is a multiple of 4, the expression is divisible by 8.
- If n is even, then (n-1) and (n+1) will be odd and the expression will be divisible by 2, 3, 4 and 6.
If p is a positive integer, what is the units digit of p?
I. p is divisible by 14, 15, 16, and n
II. (p/(17*25!)) = k, where k is an integer
If p is a positive integer, what is the units digit of p?
I. p is divisible by 14, 15, 16, and n
II. (p/(17*25!)) = k, where k is an integer
Both alone are sufficient because they show that there is at least one (5x2) pair that makes the units digit 0.
If p and q are positive integers, and n=5p + xq+4, is n a multilple of 2?
I. p = 14
II. x = 3
If p and q are positive integers, and n=5p + xq+4, is n a multilple of 2?
I. p = 14
5p is odd for any value of p as we are told in the question stem that p is a positive integer and 5 raised to any power ends in 5. We need to know the value of x to know whether the result is even or odd.
II. x = 3
Since 5P + 3q+4 is odd + odd = even, this is sufficient.
If xy > 0, is xyz < 0?
I. xz > 0
II. yz > 0
If xy > 0, is xyz < 0?
I. xz > 0
xz have the same sign, but we do not know if it is positive or negative. Not sufficient.
II. yz > 0
yz have the same sign, but we do not know if it is positive or negative. Not sufficient.
Both I & 2.
Without knowing the signs, we can’t know if the answer is positive or negative.
Scott and Jeff both purchased tickets to a certain play. If they both paid the same price per ticket andd each purchased more than one ticket, how many tickets did Scott purchase? (Assume each ticket costs a whole number of dollars more than $1.)
I. Jeff purchased $143 worth of tickets.
II. Scott purchased $187 worth of tickets.
Scott and Jeff both purchased tickets to a certain play. If they both paid the same price per ticket andd each purchased more than one ticket, how many tickets did Scott purchase? (Assume each ticket costs a whole number of dollars more than $1.)
I. Jeff purchased $143 worth of tickets.
Not sufficient because we don’t know how many tickets or how much Scott spent.
II. Scott purchased $187 worth of tickets.
Not sufficient because we don’t know how many tickets or how much Scott spent.
Both I & 2.
143 factors to 1, 11, 13 and 143. 187 factors to 1, 11, 17, and 187. Because the only common factor is 11, that must be the ticket price, this answer is sufficient.
When 999500 is divided by 5, what is the remainder?
When 999500 is divided by 5, what is the remainder?
999even power has a units digit of 1 so the remainder is 1.
even - odd =
odd
If x is an integer greater than 1. but less than 110 such that x = t4 where t is an integer, is 1/3x an integer?
I. x = m2 where m is a positive integer
II. x/2 = n where n is a positive integer
If x is an integer greater than 1. but less than 110 such that x = t4 where t is an integer, is 1/3x an integer?
The only perfect 4th powers greater than 1 but less than 110 are 16 = 24 = 42 and 81 = 34 = 92.
I. x = m2 where m is a positive integer
We already know x is a perfect square so this is not sufficient.
II. x/2 = n where n is a positive integer
x is divisible by 2 so it must be 16. Sufficient.
If a, b, and c and z are positive integers, what is the units digit of 3az * 3bz * 3cz?
I. a + b + c = 3
II. z = 4
If a, b, and c and z are positive integers, what is the units digit of 3az * 3bz * 3cz?
I. a + b + c = 3
It follows that 3(a + b + c)z = 33z. Exponent is in multiples are 3 and 33 = 27 and 36 = 729. Not sufficient.
II. z = 4
It follows that 3(a + b + c)z = 34z. Since it is a multiple of 4 and the units digit pattern of 3 is based on multiples of 4 (3-9-7-1), it will always be 1. Sufficient.
If A and D are positive integers, what is the remainder when 740A + d is divided by 5?
I. A = 5
II. D = 4
If A and D are positive integers, what is the remainder when 740A + d is divided by 5?
The units digit pattern for 7 is 7-9-3-1. Since 40 is a multiple of 40, any value of a will produce a units digit of 1. Also division by 5 always has a remainder based on the units digits distance from 5. thus we only need the value of d.
I. A = 5
Not sufficient.
II. D = 4
Sufficient.
Is the positive integer x a perfect square?
I. x = tn, where t is a positive integer and n is odd.
II. x0.5 = k, where k is a positive integer.
Is the positive integer x a perfect square?
I. x = tn, where t is a positive integer and n is odd.
n is odd so there is no way to know if the number is also a perfect square. Not sufficient.
II. x0.5 = k, where k is a positive integer.
x0.5 is the square root of x. Since it results in an integer, x must be a perfect square.
If n is an integer, is n2 - 1 divisible by 3?
I. n is not divisible by 3
II. n is divisible by 5
If n is an integer, is n2 - 1 divisible by 3?
(n+1)(n-1)
I. n is not divisible by 3
If n is not divisible by 3, then (n+1) or (n-1) must be divisible by 3 because in any group of 3 integers (4*5*6), (21*22*23), etc there is a multiple of 3. Sufficient.
II. n is divisible by 5
Using the same logic from statement 1, a multiple of 5 and 3 (15) means that neither (n+1) nor (n-1) is divisible by 3. Alternatively, 5 is not divisible by 3. Not sufficient.
If x and y are positive integers greater than one, is the smallest prime factor in x smaller than the smallest prime factor in y?
I. x = 3n
II. The least common multiple of x and y is 105
If x and y are positive integers greater than one, is the smallest prime factor in x smaller than the smallest prime factor in y?
I. x = 3n
This tells us the only prime factor is 3, but there is no information about y. Not sufficient.
II. The least common multiple of x and y is 105
The prime factors are 3*5*7, but no information is provided on which is x and which is y. Not sufficient.
Both I & II.
Y must contain 5*7, but it could also contain a 3 since LCM multiplies by the highest number, each can have a 31 that is only used one. . Not sufficient.
There is a certain number of students in Mr. Stewart’s class. Could Mr. Stewart evenly divide the class into 3 study groups?
I. If Mr. Steward reduced the number of students in his class by 16%, he could evenly divde the class into groups of 9.
II. If Mr. Steward reduced the number of students in his class by 6% he could evenly divide the class into groups of 3.
There is a certain number of students in Mr. Stewart’s class. Could Mr. Stewart evenly divide the class into 3 study groups?
I. If Mr. Steward reduced the number of students in his class by 16%, he could evenly divde the class into groups of 9.
84/100x = 21/25x => (21/25)x/9 = 7x/(25*3). Because 3 does not divide into 7, he must be able to split the original class (x) into 3 groups. Sufficient,
II. If Mr. Steward reduced the number of students in his class by 6% he could evenly divide the class into groups of 3.
94/100x = 47/50x => (47/50)x/9 = 47x/(50*3). Because 3 does not divide into 47, he must be able to split the original class (x) into 3 groups. Sufficient.
If x and y are positive integers and y < 5x, the remainder is z when 5x is divided by y. What is the value of z?
I. When y + 1 is divided by 5, the remainder is 1.
II. When y + 1 is divided by 4, the remainder is 2.
If x and y are positive integers and y < 5x, the remainder is z when 5x is divided by y. What is the value of z?
5x/y = q + z/y
I. When y + 1 is divided by 5, the remainder is 1.
Y is a multiple of 5. Test numbers.
5(1)/5=1 and 15x/10= 1 + 5/10. Not sufficient.
II. When y + 1 is divided by 4, the remainder is 2.
5(2)/5 = 1 + 2/5. 5(2)/9= 1 + 1/9. Not Sufficient.
Both I & 2.
Y could be 5 or 25. 30/25 = 1 + 1/5 and 35/25 = 1 + 2/5. Not sufficient.
Terminating Decimals Question
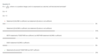
Terminating Decimals Question
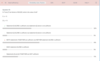
Divisibility Rules and Factors Question

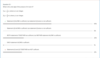
Units digits of factorials
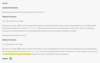
Prime Factorization of a perfect square will contain only even exponents
Number of unique factors in a number does not change when that number is raised to a positive integer exponent.


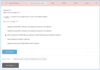
Summary of Multiplication and Division
Divisibility

Terminating Decimals
Trailing Zeroes
Patterns in units digits

The beginning of the solution is cut off. See Number Properties -> Hard Test # 7

Remainder Patterns in Powers


Prime Factorization of Perfect Squares and Cubes


Patterns in Units Digits


Division Properties of Factorials

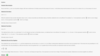
A second approach to finding LCM


Prime Factorization


A Formula for Division


Finding the GCF


Comparing Size: Roots
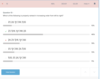

Data Sufficiency: Negative Square Roots
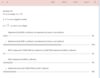

Data Sufficiency Practice


What is the greatest integer value that 4n is a factor of 31!-30!?

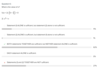

What is the greatest possible integer value of n such that 9n is a factor of 43! + 44!?


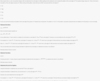
1/6
.167 or 16.7%
1/7
.142 or 14.2%
1/8
.125 or 12.5%
3/8
.375 or 37.5%
7/8
.875 or 87.5%
5/6
.833 or 83.3%
1/9
.11%
Base 9 fractions, what happens after 4/9?
It follows multples of 11 after the decimal point, and then it’s +1
1/9 = .11
2/9 = .22
3/9 = .33
4/9 = .44
5/9 = .56
6/9 = .67
7/9 = .78
8/9 = .89
1/12
0.083 or 8.3%
5/12
0.42
7/12
.58
11/12
.92
1/7
.143
2/7
.29
3/7
.43
4/7
.57
5/7
.71
6/7
.86
Pattern in Base 11 fractions
Multiples of 9 until after 5/11, then it’s +1
1/11 = 0.09
2/11 = 0.18
3/11 = .27
4/11 = .36
5/11 = .45
6/11 = .55
7/11 = .64
8/11 = .73
9/11 = .82
10/11 = 0.91
1/13
0.08
Base 13 fraction patterns
1/13 (0.08) -> 4/13 => multiples of 8
5/13 (.38) -> 8/13 => multiples of 8 - 2
9/13 (.69) -> 11/13 => multiples of 8 - 3
12/13 (.92) => multiple of 8 - 4
1/15
.07
2/15
.13
4/15
.27
7/15
.47
8/15
.53
11/15
.73
13/15
.87
14/15
.93
1/25 and 2/25
0.04 and 0.08
Base 20 fraction patterns
All base 1/6 - 1/9 fractions
1/6 = .167
1/7 = .142
1/8 = .125
1/9 = .11
1/8 and 3/8 and 7/8
1/8 = .125
3/8 = .375
7/8 = .875
How does the factorial division shortcut work when you have factored and get a non-factorial, (e.g., 30!(30))
Use the standard factorial divsion shortcut for the factorial, but then prime factor. the non-factorial to get the number of primes in that & add
Greatest value of 4n such that 31! - 30! = k where k is integer.
- Factor 31! - 30!
- 30! (31-30) = 30!(30)
- For the factorial, use the factorial divsion shortcut of the highest prime number of 4
- Factorial: 30!/2=15, 30!/22=7, 30/23=3, 30/24=1
15 + 7 + 3 + 1 = 26
- Prime factorize 30 into 2 * 3 * 5
- 27 twos, but because it is 4, must divide by 2 = 13.5 so 13 is the highest possible value for n
Determining if a number is a perfect square
It will end in 0, 1, 4, 5, 6 or 9.
The Digital summation will be 1, 4, 7, 9
Digital summation example: 961 =6+1+9=16=1+6=7
N2/m = integer, what must be true about the number of unique prime factors of m?
N2/m = integer, what must be true about the number of unique prime factors of m?
It must have the same or less than the number of unique prime factors as N, otherwise it would not equal an integer
Is the product of p and q a multiple of 7?
I. the LCM of p and q is 80
II. the GCF of p and q is 4
Statement I. LCM tells us that 7 is not a prime factor and therefore is not a multiple of 7.
It’s not GCF because 4 and 28 have a gcf of 4 and is a multiple of 7 but 8 and 4 have a GCF of 4 but is not a multiple of 7.
|a-b| > |a+b| means the signs are _______ and as a data sufficiency question this can be rewritten as
|a-b| > |a+b| means the signs are opposite and as a data sufficiency question this can be rewritten as quadratic equations by square both sides
a2-2ab+b2>a2+2ab+b2
is ab>0?


