5 - Roots and Exponents Flashcards
(115 cards)
1
Q
02
A
0

2
Q
Perfect Cubes 1-10
A

3
Q
Non-perfect Square Roots to Memorize
A
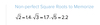
4
Q
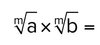
A
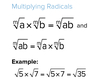
5
Q
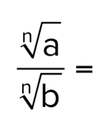
A

6
Q
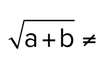
A
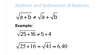
7
Q
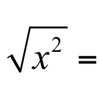
A
NOTE: On the GMAT, it’s not the absolute value when it’s not a variable
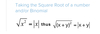
8
Q
Bases of 2
A

9
Q
Bases of 3
A

10
Q
Bases of 4
A

11
Q
Bases of 5
A

12
Q
Multiplication of Like Bases

A

13
Q

A

14
Q
(XA)B
A

15
Q
12
A
1
16
Q
22
A
4
17
Q
32
A
9
18
Q
42
A
16
19
Q
52
A
25
20
Q
62
A
36
21
Q
72
A
49
22
Q
82
A
64
23
Q
92
A
81
24
Q
102
A
100
25
112
121
26
122
144
27
132
169
28
142
196
29
152
225
30
22
4
31
23
8
32
24
16
33
25
32
34
26
64
35
27
128
36
28
256
37
29
512
38
210
1024
39
53
125
40
54
625
41
33
27
42
34
81
43
35
243
44
43
64
45
44
256
46
(xa)(ya) =
(xy)a
47
xa/ya =
(x/y)a
48
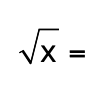
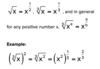
49
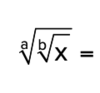

50
Nonzero Based Raised to the Zero Power
When a non-zero base is raised to the zero power, the expression equals 1. (e.g., 20 = 1)
51
Any base raised to the first power
Any base raised to the first power, the value equals that base. (e.g., 21=2)
52
x-1 =
1/x and in general, x-y= 1/xy
Examples:
2-2 = 1/22=1/4
1/33=3-3
(3/7)-3=(7/3)3
53
Adding or subtracting expressions with exponents
210 + 211 + 212
When adding or subtracting expressions with exponents, consider factoring out the common factors.
210 + 211 + 212
=\> 210(1 + 21 + 22) = 210(7)
54
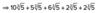

55
2n + 2n =
2n + 2n = 2n+1
3n + 3n + 3n = 3n+1
4n + 4n + 4n + 4n = 4n+1
The rule continues on forever with different bases (number of terms must equal base).
56
**Exponent Number Properties Case #1**
_Base:_ \> 1
_Exponent:_ even positive integer
52
**Exponent Number Properties Case #1**
_Base:_ \> 1
_Exponent:_ even
*=\> Result is larger*
52 \> 5
57
**Exponent Number Properties Case #2**
_Base:_ \> 1
_Exponent:_ odd positive integer \> 1
53
**Exponent Number Properties Case #2**
_Base:_ \> 1
_Exponent:_ odd positive integer \> 1
*=\>Result is larger*
53 \> 5
58
**Exponent Number Properties Case #3**
_Base:_ \< -1
_Exponent:_ even positive integer
(-4)2
**Exponent Number Properties Case #3**
_Base:_ \< -1
_Exponent:_ even positive integer
*=\>Result is larger*
(-4)2 \> 4
59
**Exponent Number Properties Case #4**
_Base:_ \< -1
_Exponent:_ odd positive integer
(-5)3
**Exponent Number Properties Case #4**
_Base:_ \< -1
_Exponent:_ odd positive integer
* =\> Result is smaller*
- (5)3 \< -5
60
**Exponent Number Properties Case #5**
_Base:_ positive proper fraction
_Exponent:_ even positive integer
(1/5)2
**Exponent Number Properties Case #5**
_Base:_ positive proper fraction
_Exponent:_ even positive integer
*=\> Result is smaller*
(1/5)2 \< (1/5)
61
**Exponent Number Properties Case #6**
_Base:_ negative proper fraction
_Exponent:_ even positive integer
(-1/5)2
**Exponent Number Properties Case #6**
_Base:_ positive proper fraction
_Exponent:_ even positive integer
*=\> Result is larger*
(-1/5)2 \> (-1/5)
(Remember a fraction multiplied by another fraction gets closer to 0 on the number line)
62
**Exponent Number Properties Case #7**
_Base:_ positive proper fraction
_Exponent:_ odd positive integer \> 1
(1/5)3
**Exponent Number Properties Case #7**
_Base:_ positive proper fraction
_Exponent:_ odd positive integer \> 1
*=\> Result is smaller*
(1/5)3
63
**Exponent Number Properties Case #8**
_Base:_ negative proper fraction
_Exponent:_ odd positive integer \> 1
(-1/5)3
**Exponent Number Properties Case #8**
_Base:_ negative proper fraction
_Exponent:_ odd positive integer \> 1
*=\> Result is greater*
(-1/5)3 \> -1/5
(Remember that multiply a fraction by a fraction moves it closer to 0 on the number line.)
64
**Exponent Number Properties Case #9**
_Base:_ \>1
_Exponent:_ positive proper fraction
51/2
**Exponent Number Properties Case #9**
_Base:_ \>1
_Exponent:_ positive proper fraction
*=\> Result is smaller*
51/2 \< 5
65
**Exponent Number Properties Case #10**
_Base:_ positive proper fraction
_Exponent:_ positive proper fraction
1/51/2
**Exponent Number Properties Case #10**
_Base:_ positive proper fraction
_Exponent:_ positive proper fraction
*=\> Result is larger*
1/51/2 \> 1/5
(1/5 = 0.2, 1/51/2 = 0.45)
66
Square Roots of Large Perfect Squares (Trailing Zeroes)

67
Square Roots of Small Perfect Squares (Leading Zeroes)

68
Cube Roots of Large Perfect Cubes (Trailing Zeroes)

69
Cube Roots of Small Perfect Cubes (Leading Zeroes)

70
5x+1 =
5x \* 5
71
Cube Root of 4 over Cube Root of 4 over Cube Root of 4
41/3 \* 41/(3)^2 \* 41/(3)^3
=\> 49/27 \* 43/27 \* 41/27 = 413/27
72
3 Square Roots of .00000256
1. Take the square root of perfect cube and halve the decimals
2. Repeat for each additional square root symbol
Square root of .00000256 = .0016
=\>Square root of .0016 = .04
=\>Square root of .04 = .2
(It is similar to a function where perform the first operation and then use the result to enter into the next operation).
73
Factor Exponential Equation
5x - 5x-1 = 500
What is (x-1)2?
5x - 5x-1 = 500 and solve for
1. On the left side, factor to simplest form. =\> 5x - (5x)(5-1) =\> 5x(1 - 5-1)
=\> 5x(1 - 1/5) =\>5x(4/5)
2. Raise entire equation to eliminate fractions =\> 5(5x(4/5) = 500)
=\> 5x(4) = 500
3. Factor to get equal bases =\> 5x22 = 5422 =\> 5x=54 =\> x=4
4. Plug in 4 into the equation (x-1)2 =\> (x-1)(x-1) =\> x2 - 2x + 1 =\> 42 - 2(8) + 1 = 9
(4-1)2 also works because you have a derived value of x, however you would need to factor and solve for the quadratic if you did not have the x value.
74
What is 7/radical(7)?
radical(7), it's the reverse of radical(7)\*radical(7)=7
75
Radical(7)/7
1/radical(7)
76
What is a tactic for matching the answer choices of exponents?
Be aware of what the answer choices are and merge/split as needed
77
Simplify:
numerator: _(1/x4 -x2)_
denominator: 1-x6
1. Get a common base of x4 in numerator. Note that x6/x4 = x2. numerator: _(1/x4 - x6/x4)_
denominator: 1 - x6
=\> numerator: _(1 -x6/x4)_
denominator: (1-x6)
2. Divide numerator and denominator.
numerator _1-x6 \* 1_
denominator: x4 \* 1-x6
3. 1-x6 cancels out. Simplify to get rid of the fraction.
=\> 1/x4 = x-4
78
numerator: _(1197 \* 742 \* 572 \* 331 \* 450)_
denominator: k
Which of the following could be the value of k if the result is an integer?
A. 11100 - 1198
B. 745 - 743
C. 574 - 573
D. 334 - 332
E. 299 - 296
E. 299 - 296
Because it is less than 450 = (22)50 = 2100. All other values exceed their respective primes.
79
Simplify:
(23p + 23p + 23p + 23p )(33p + 33p + 33p + 33p + 33p + 33p + 33p + 33p + 33p)
(23p + 23p + 23p + 23p )(33p + 33p + 33p + 33p + 33p + 33p + 33p + 33p + 33p)
=\> 23p(1 + 1 + 1 +1) 33p(1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1)
=\> 23p(4) 33p(9)
=\> 23p(22) 33p(32)
=\> 23p+233p+2
=\> **63p+2**
80
Radical in the denominator.
A radical in the denominator is not considered simplified. You need to "rationalize" the radical.
numerator: _3 + radical(5)_
denominator: radical(5)
1. Multiply by radical(5)/radical(5)
=\> numerator: _3 + radical(5) (radical(5))_
denominator: radical(5)(radical(5))
=\> numerator: _3radical(5) + 5_
denominator: 5
Done!
81
How do you remove a radical in a binomial?
Multiply by the conjugate (change the sign of the binomial).
numerator: _4_
denominator: a - radical(b)
1. Multiply by conjugate = a+radical(b)
=\> numerator: _4(a+radical(b)_
denominator: (a - radical(b))(a+radical(b))
=\> numerator: _4a + 4(radical(b))_
denominator: a2 - b
82
Exponents in some cases may not be equal even when they appear to be. How can you mitigate this?
Test with 0, 1, -1 on data sufficiency questions.
83
Exponents are distributed over which operations?
Multiplication and division.
(4abc)2=42a2b2c2
(12/15)2 = 122/152
84
What is the square root and cube root of x in fraction form?
Square root of x= x1/2
cube root of x=x1/3
numerator = power of the radicand
denominator = index
Cube root of x5 = x5/3
85
Square root of 5 is approximately?
2.2
86
Square root of 6 is approximately?
2.4
87
Square root of 7 is approximately?
2.6
88
Square root of 8 is approximately?
2.8
89
Square root of 2 is approximately?
1.4
90
Square root of 3 is approximately?
1.7
91
60th root of x = 10th root of 2
Solve for x.
1. Rewrite as fractions.
x1/60 =21/10
2. Multiply by LCD
60(x1/60 =21/10) =\> x60/60 = 260/10 =\> x1 = 26
**=\> x=64**
92
Which is larger 550 or 725?
Multiply exponent (only) by 1/gcf.
550(1/25) and 725(1/25) =\> 52 and 71
550 is larger.
93
Exponential notation can be factored
41000 = 4 \* 4 \* 4 \* 499
94
Change (1/2)-2 to a positive exponent and solve.
Flip the fraction and change the sign of the exponent.
(2/1)2=4
95
Pemdas for exponents - what is first, distributing the negative sign or the exponent?
-26 - 33
Exponent.
-26 - 33
-64 - 27= -91
96
Solving equations with square roots
1. Isolate the radical to one side
2. square the equation
3. solve
4. **must** check the answer back in the equation
97
Roots in inequalities
Roots should generally not be in inequalities unless it is an odd root
98
210 + 210 =
211
99
Scientific notation - multiplying co-efficients
(3.5 \* 105)(40 \* 106)
Co-efficients can be multiple or divided separately to make the calculation easier
(3.5 \* 105)(40 \* 106)
(.35 \* 106)(4.0 \* 107)
.35\*4=1.4
1.4 \* 1013
100
Scientific Notation
6 \* 106
and
6.4 \* 10-6
6 \* 106= 6,000,000 (add 6 zeroes)
and
6.4 \* 10-6=.0000064 (move decimal 6 places to the left
101
Powers can only be used in what two types of inequalities?
1. All terms are positive
2. When the power is odd (because it won't change the sign of the term)
102
Factor exponential equation
162x \* 324 = 1
Factor exponential equation
162x \* 324 = 1
Move to common base of 2 (20 = 1)
(24)2x \* (25)4 = 20
28x \* 220 = 20
8x+20=0
8x=-20
x=-20/8 = -5/2
103
Requirement to multiply radicals
must have the same index. If not, convert to a fraction and find the lcd (I think).
104
(1610 - 234)/21n
What is the largest possible value for n?
(1610 - 234)/21n
## Footnote
=\> (240 - 234)/21n =\> 234(26-1)/21n=\> 234(63)/21n =\> 234(21x3)/21n
Only one value of 21 so the largest value of n possible is 1.
105
radical(81/1/x)=x
what is x?
radical(81/1/x)=x
radical(81\*x/1) = x =\> radical(81x)=x
With the radical on one side and the fraction removed, you can square the equation.
81x=x2
It's a quadratic (raised above the power of one) so set the equation equal to zero and solve. .
81x - x2 = 0
x(81-x)
x=0, x=81
106
Factor
2x+1
and
2x-1
2x+1 = 2x \* 21
and
2x-1 = 2x \* 2-1
107
Data Sufficiency: Trailing Zeroes


108
Complex Roots


109
Quadratic Exponents as Expressions
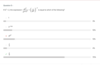

110
Trailing Zeroes in Exponenets #2


111
Data Sufficiency: if bases are equal, exponents may be equal

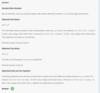
112
Complex exponent changes


113
Complex Roots / "no larger than" integer divisibility
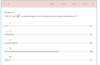

114
Data sufficiency 0/1 bullshit

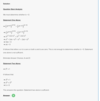
115
(7\*10^9)(7\*10^3)
(7\*109)(7\*103)
49\*1013
=\>4.9\*1014


