Week 2 Economic growth

Question 1

What are some basic facts about Economic growth?

Answer 1

Richer countries do not tend to grow faster than poorer countries

Before the industrutiral revolution, there were little differences between countries overtime.

After the Industrial revolution, per capita income growth has veen growing sustainially in the richest countries.

• There is a negative correlation between the population growth rate and output per worker across countries.

Question 2

What thoery tries to explain economic growth?

Answer 2

The solow growth model

Question 3

What is a key prediction of the solow growth model?

Answer 3

You can have sustained economic growth from technological improvements over time.

Question 4

What assumption will we use for the solow growth model in terms of people, firms and government?

Answer 4

We will have an identical firm, consumer and there will be no government in this model

Question 5

What assumption of the solow growth model will we have in terms of the goods produced and exchanged?

Answer 5

One homogenous good ie a cookie, can be transformed into investment goods (1:1) one cookie will transform to a engineering plant. Consumers dont care about lesiure.

Question 6

What assumption of the solow growth model will we make about the peoples preferences of goods?

Answer 6

People don’t care about lesiure, people consume a constant fraction (1-s) of their income and sace the rest.

C = (1-S)Y s<1

S = sY

Question 7

What assumption of the solow growth model will be assume in terms of the technology avaliable to firms?

Answer 7

Firms produce their output using a production function

Y = zF(K,N)

where Z = TFP, how effective is the production process, the higher the z the more efficient you are at combining capital and labour.

K = capital input

N = labour input ( each worker works 247

F = function

Question 8

What assumptions of the solow growth model will we assume in terms of the resources avaliable in the economy. As consumers dont value lesiure whats their labour supply too.

Answer 8

We start with inital capital and labour inputs

K0 and No ( each worker has one unit of labour to offer to firms)

Overtime the number of people in the economy will change

(next period)N’ = (1+n)N

N represents both the number of workers and the population at beginning of the year

n = the poplutation growth rate ( for the next year

Consumers do not value lesiure so labour supply = 1.

K’ = (1-d)K+l

(1-d) is the number of capital depreciated to be left with what is left at the end of the year X K which is the the capital at the beginning of the year)

I = investment made for the next year will affect how much capital will grow next year

Question 9

What are the end rules of the game?

Answer 9

Firms want to maximise profits

Consumers consume and save

Competitive equilbrium

Question 10

Now looking at the production function, what are we going to assume about the production function, first of all lets make a zombie cafe example to prove the point?

Answer 10

Y = zF( K,N)

To produce cofee we need labour and capital inputs ( workers and cofee machine)

Lets say 1 worker and 1 coffee machine can produce output of 12

Lets say a second worker and 1 cofee machine produce an output of 20 cofees ( so 8 more coffees)

Lets say a 3rd worker and 1 cofee machine produces an output of 24 cofees in total ( 4 more coffess)

Same thing when I have 2 coffee machines and 1 worker i produce 18 coffees, when i increase the number of workers, output will increase but at a diminishing rate?

Question 11

What does the cofee example tell us about the production function?

Answer 11

The increase that we have in the production from an additional unit of labour is called the Marginal product of labour, we assume it is positive everytime i hire another person, but at a diminishing rate.

Vice verse for the Marginal product of capital, it increases at a diminishing rate.

Question 12

What is another property of the production function?

Answer 12

If i double the inputs i.e workers and cofee machines, my output will double e.g. from 12 to 24. This is called constant returns to scale.

Question 13

What is the partial deratives of with respect to labour and capital of the production functions?

Answer 13

Question 14

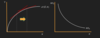
How do we illustrate the production function on a diagrams keeping capital fixed, to isolate, the labour input?

Answer 14

The slope of this is the production function is the marginal product of labour, we see the same thing on the diagram on the right, as the amount of labour increases, the MPn decreases.

Question 15

How do we illustrate the production function on a diagrams keeping labour fixed, to isolate, the capital input?

Answer 15

Question 16

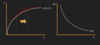
What other assumption can we make about the Marginal product of captial and labour?

Answer 16

The marginal product of labour will be higher if we increase capital

The marginal product of capital will be higher if we incrrase labour.

This is the same vice versa

Question 17

Showcase constant returns to scale assumption?

Answer 17

2Y = zF(2k, 2N)

If i double the amount of capital and workers i hire, i get double the output, if i half the capital and workers i hire, i get half the output.

Question 18

Now would i demonstrate Output per worker using the production function and define some variables?

Answer 18

Y = Y/N = ( output per worker)

K = K/N ( capital per worker)

F(k) = F(K/N,1) capital per worker with labour inputs 1.

Question 19

Thus, what can the production function be written as?

Answer 19

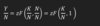
Y = zf(k)

this tells that the output per worker depends on the total factor productivity x the capital per worker.

Question 20

How does Y = zf(k) look like?

Answer 20

Question 21

So now we want to have all of the variables in per worker quanitities? but first now list all the equations we are going to need?

Answer 21

K’ = (1-d)K + I

Y=zF(K,N)

Y = C + I +G+ Nx ( WE ASOME THERE IS NO GOVERMENT AND NO INTERNATIONAL TRADE SO

Y= C+I instead of add G+Nx

4) Consumers either consume or save Y = C+S
5) 𝑆 = 𝑠𝑌, 𝐶 = (1 − 𝑠)Y

Question 22

So we want an equation that tells us how capital per worker next year is going to beb affected by capital per worker this year. Using this equation solve this K’ = (1-d)K + I .

1) K’ = (1-d)K + I
2) Y=zF(K,N)

Y = C + I +G+ Nx ( WE ASSUME THERE IS NO GOVERMENT AND NO INTERNATIONAL TRADE SO

3) Y= C+I instead of add G+Nx
4) Consumers either consume or save Y = C+S
5) 𝑆 = 𝑠𝑌, 𝐶 = (1 − 𝑠)Y

Answer 22

1)Y = C + I

Y = C+S

this implies I=S ( output saved by consumer will be transformed to investment goods, which adds to capital stock of the economy)

2) I can use equation 5,6 and 2 to get

I = szF( K,N)

3) Now you can plug what investment is into equation 1

K’ = szF(K,N) + (1-d)k

4) Now i will divide by N

Question 23

What is the next step, that tells me how capital per worker next year is affected by capital per worker this year?

Answer 23

K’/N is not capital per worker next year, it would have to be K’/N’ so we times this by population next year (N’/N’) to get (1+n)k’=

szF(K.N) = szF(K/N, N/N) = szf( K/N , 1) + (1-d)K/N

then follow the steps and get the answer.

Question 24

How does capital per worker next year in terms this year look on a diagram?

Answer 24

It looks very similar to the production function.

Question 25

How can we use this diagram to show how captial per worker evolves in this theory?

Answer 25

This function with the 45* line tells us what capital per worker will be next year, you start with an inital level of capital , then to find out capital per worker in year 2, you draw a line horizontal up to the 45 degree line, then you keep plugging in the functions to find it the next coming years.

Question 26

What can we say about captial per worker over time?

Answer 26

Capital per worker is growing over time, meaning output per worker is growing over time, thus living standards is growing over time. Notice they are growing at a diminishing rate though ( e.g. Ko to K1 > K1 to K2.

Question 27

Do we grow forever by making capital per worker increase and increase?

Answer 27

No, at some poiny the growth rate becomes smaller and smaller and growth stopes, this is where we reach K*, the next year the growth rate is 0, this is called the steady state.

Question 28

How will the steady state equation look like?

Answer 28

Question 29

At the steady state was is happening

Answer 29

Investment per worker = Depreciation per worker ( thus the capital stock per worker is neither rising or falling.

Question 30

When i do some rearrangments on this equation what would i get? and what does this mean

Answer 30

The value of capital per worker at the steady state will be determined by this equation

This equation tells me : on the left hand side i have investment per worker ( so the new amount of capital the economy is making for each worker) the right hand side tells me that i have capital per worker K* and every year i have to cover for 2 things, when deciding how much investment to do, each year you will have more workers and some machines will break down

Question 31

How can i plot the steady state equation on a diagram?

Answer 31

We plot both sides of the equation

If we are on the left of the steady state it means investment is greater than depreciation meaning capital stock is growing, If we are on the right of the steady state it means investment is lower depreciation, meaning capital stock is strinking

Question 32

What does thee steady state equation tell you?

Answer 32

Tells you the capita per worker in the steady state is determined by the savings rate S, the z total factor productivity, the growth rate of the population n and the depreciation rate d.

If i want to find the value of the capital per worker in the steady state i need to know these numbers.

Question 33

What happens if S goes up ( savings/ investment ) and what about TFP?

Answer 33

The slope of szf(k*) depends on s and marginal product of capital, if i increase s, the slope at every level of capital per worker will be a bit higher.

If there is higher savings, we will stop growing a later on meaning a higher capital per worker and living standards

The same shift will happen for Z.

Question 34

What happens when n goes down?

Answer 34

The slope will be lower still through the orgin, but with higher level of capital per worker at the steady state.

Question 35

Lets summarise what happens to the steady state capital per worker, when there is an increase in S,Z, n and d

Answer 35

Increase in Savings - K* will increase

Increase in Z - K* will increase

Increase in n - K* will decrease

Increase in depreciation K* will decrease.

Question 36

So far we have looked at capital per worker, which will determiine output per worker, which determines living standards, and consumption per worker is a fraction of output per worker, and in the steady state they stop growing. What about Aggregrate variables, which are?

Answer 36

Capital, GDP and Consumption

Question 37

Summarisr what we know about the steady state and what it implies?

Answer 37

In steady state captial per worker is constant ( k*), thus output per worker is constant y = zf(k*), this also implies consumption per worker is constant C* = (1-s)y*

Question 38

We have said that capital per worker at steady state is the ratio of K* = (K/N)* (CAPITAL I HAVE, DIVIDED BY POPULATION), in the steady state we are saying this number is constant, is it constant?

Answer 38

N is not constant it grows every year N’ = (1+n)N, so this implies that aggregrate capital is growing at the same rate as aggregrate population, when we are in the steady state,

We can do the same reasoning for K, Y AND C variables, all these variables are growing in the steady state at a rate N, the population growth rate

Question 39

Capital per worker What happens when we are not in the steady state ?

A. If capital per worker is lower than 𝑘 ∗ , then living standards growth rate is positive

B. If capital per worker is lower than 𝑘 ∗ , then aggregate capital growth rate is negative

C. If capital per worker is higher than 𝑘 ∗ , then living standards growth rate is positive

D. If capital per worker is lower than 𝑘 ∗ , then living standards growth rate increases over time

E. If capital per worker is lower than 𝑘 ∗ , then aggregate capital growth rate decreases over time until it reaches zero

F. If capital per worker is lower than 𝑘 ∗ , then aggregate capital growth rate decreases over time until it reaches n

Answer 39

A and F and maybe D

Lets look at A - C

The diagram on the left shows that we start from an inital level of capital k0, then draw horizontal lines to find k1 k2 and k3 to get the curve, getting closer and closer to the steady state ( as you can see capital per worker will grow faster at the beginning the increasing slowly ( MPk is diminishing) So A is right,

we can also see this in the capital per worker growth rate diagram where we do for the each year, percentage increase e.g. for yr 1 k1 - k0/k1 and second year k22-k1/k1.

Question 40

Aggregrate variables What happens when we are not in the steady state ? E-F

A. If capital per worker is lower than 𝑘 ∗ , then living standards growth rate is positive

B. If capital per worker is lower than 𝑘 ∗ , then aggregate capital growth rate is negative

C. If capital per worker is higher than 𝑘 ∗ , then living standards growth rate is positive

D. If capital per worker is lower than 𝑘 ∗ , then living standards growth rate increases over time

E. If capital per worker is lower than 𝑘 ∗ , then aggregate capital growth rate decreases over time until it reaches zero

F. If capital per worker is lower than 𝑘 ∗ , then aggregate capital growth rate decreases over time until it reaches n

Answer 40

We start with a growth rate of aggregrate capital higher than n at the inital period then will slowly go down untill it reaches n or the steady. ( aggregrate capital grows faster than population then slowly aggregrate capital goes down then the ratio balances ( so growth rate is n) )

Growth rate of Aggregrate variables below the steady state decreases untill it reaches n.

Question 41

With aggregrate variables such as GDP, consumption etc, when they a far from steady state what happens?

Answer 41

When far from the steady state, they start growing at a rate higher than n, then thisi growth rate gors down untill we reach the steady state ahd then the aggregrate variables growth rate = n.

Question 42

What happens to capital per worker, growth rate of captial per worker, GDP per worker, consumption per worker, Aggregrate capital natural log, GDP natural log, when we start from an initial level of capitial at the steady state.

Answer 42

When we are in the steady state, we stay there

Question 43

What happen scapital per worker, growth rate of captial per worker, GDP per worker, consumption per worker, Aggregrate capital natural log, GDP natural log, if we are the steady state for 20 years and savings go up?

Answer 43

The steady states jumps up after 20 years, so MPk is higher after new steady state then grows slowly to the new steady state.

With consumption ( if you save more, this means c = (1-s)Y goes down.

Question 44

What happen scapital per worker, growth rate of captial per worker, GDP per worker, consumption per worker, Aggregrate capital natural log, GDP natural log, if we are the steady state for 20 years and TFP increases?

Answer 44

For 20 years, nothing happens, then, At every level of capital each worker is more productive, the steady state is higher with higher capital per worker but growth rate decreases slowly after time. GDP per worker increases as i am able to produce more, meaning i can consume more ( remember consumers owns firms)

Question 45

What happens capital per worker, growth rate of captial per worker, GDP per worker, consumption per worker, Aggregrate capital natural log, GDP natural log, if we are the steady state for 20 years and there is an increase in population growth rate?

Answer 45

The capital per worker in the steady state will be lower, os llibing sttandards, will go down and consumption wiill go down

Growth rate is negative.

Notice with aggregrate variables, they will go to a new steady state path, having a new growth rate, we are growing at a higher growth rate as the population growth rate is higher. (slope changes)

Question 46

What are 2 ways for temporary increase in living standards again?

Answer 46

1) Increase saving rate = higher capital per worker, higher level of GDP ( problem you cant increase saving rate forever, you need consumption)
2) Reduce population growth rate ( e.g demographic policies, we reduce amount of people)

Changing s and n have temporary effects on libing standards.

Question 47

How do we get sustained long run economic growth?

Answer 47

Technological advances, improvement of TFP and better processes ( TFP needs to grow forever)

Question 48

So far in our model what have we done to TFP?

Answer 48

We have kept it constant

Question 49

Lets say TFP grows constantly each year what is the equation of tfp for next year?

Answer 49

Question 50

What happens capital per worker, growth rate of captial per worker, GDP per worker, consumption per worker, Aggregrate capital natural log, GDP natural log, if we are the steady state for 20 years and there is an increase in TFP at a constant rate?

Answer 50

Every year the capital per worker steady state is going to be higher and higher, growth rate stays positive forever. Consumption per worker grows expotentially, GDP per worker grows expotentially

Question 51

How do we get TFP to grow over time?

Answer 51

We can think of TFP growth coming from innovations, which is a public good, but as a inventor whats the incentive to promote new technological advances.

Question 52

What are policies to promote technological advances?

Answer 52

Patent laws

Question 53

What are 2 extra determinants ofTFP?

Answer 53

Human capital ( investing human capital, increases productivity)

Health and nutiriton ( countires with good healthcare have higher productivity)

Question 54

Winterfell and King’s Landing are both agricultural economies that use workers and capital (in the form of agricultural equipment, livestock and farms) to produce food. They have recently been ravaged by the White Walkers, which are zombie creatures coming from the North. The effects of their passage however has been different in the two kingdoms.
In Winterfell, the White Walkers have killed (and trasnsformed into zombies) scores of peasants, leaving the farms and the livestock intact. In King’s Landing, instead, the damage has been to farms and agricultural equipment, but people were safe inside the wall of the city. Mark the correct answers:

Select one or more:

a. The living standards of Winterfell will go down in the long run. The living standards of King’s Landing will go up in the long run.
b. The living standards of Winterfell and King’s Landing will not be affected in the long run.
c. In the few years after the descent of the White Walkers, economic growth will slow down in Winterfell, while King’s Landing will experience a higher growth rate.
d. In the few years after the descent of the White Walkers, economic growth will slow down in Winterfell and in King’s Landing.
e. In the few years after the descent of the White Walkers, the economic growth rate will be higher both in Winterfell and in King’s Landing.