Variable Changes and the Jacobian.

Question 1

When is a scalar field f(x) : U ➝ ℝ, U open in ℝⁿ differentiable at a ∈ U?

Answer 1

Question 2

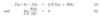
What term is linear in h in the following?

Answer 2

Question 3

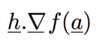
When is a vector field F(x) : U ➝ ℝⁿ, U open in ℝⁿ differentiable at a ∈ U?

Answer 3

If there is a linear function L : ℝⁿ ➝ ℝⁿ such that

Question 4

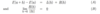
If we write the j^th component of the following?

Answer 4

Question 5

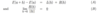
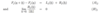
How else can we write L_j(h)?

Answer 5

Question 6

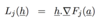
Using the following equation how do we write L in matrix form

Answer 6

Question 7

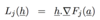
What is the following matrix called?

Answer 7

The Jacobian

Question 8

What is the Jacobian matrix?

Answer 8

Question 9

What is another name for the Jacobian matrix?

Answer 9

Differential of F(x)

Question 10

What symbol do we use to represent the Jacobian matrix?

Answer 10

DF(a)

Question 11

Define Jacobian.

Answer 11

Question 12

What can you think of a vector fled v(x) as?

Answer 12

Coordinate transformation on ℝⁿ

Question 13

What can you think of v(a + h) - v(a) as?

Answer 13

Transformed coorindates relative to the transformed origin v(a)

Question 14

What is v(a + h) - v(a) roughly equal to?

Answer 14

Question 15

What is the inverse function theorem?

Answer 15

Question 16

Define diffeomorphism and diffeomorphic.

Answer 16

Question 17

Define local diffeomorphism.

Answer 17

Question 18

Suppose the following. What does this suggest w(v(x)) is?

Answer 18

Question 19

What is Dw(v(x)) equal to?

Answer 19

Question 20

What does D(w(v(x)) equal when v is a local diffeomorphism and w is its inverse map?

Answer 20

Question 21

What does D(v)^-1 equal when v is a local diffeomorphism and w is its inverse map?

Answer 21

D(w)

Question 22

Define orientiation preserving and orientation reversing .

Answer 22

Question 23

How do the determinants relate in the following equation.

Answer 23