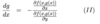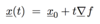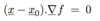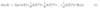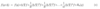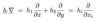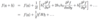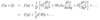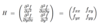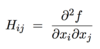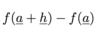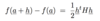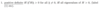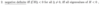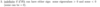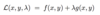Differentiability of Scalar Fields Flashcards
Define
Define continuous.
Finish this theorem: If f and g are continuous at a then so are … ?
- f + g
- fg
- f/g provided that g(a) ≠ 0
Define an open ball.
Define an open set.
A subset S of ℝn is open (S is an open set) if for each point a ∈ S there is an open ball Bδ(a) which is also in S.
Define a neighbourhood.
A neighbourhood N os a point a ∈ ℝn is a subset of ℝn which includes an open set containing a.
Define a closed set.
Prove every open ball Bδ(a) in ℝn is open .
Need to do
Define continuous on U (U is an open subset).
If U is an open subset of ℝn and f:U ➝ ℝ is a function then f is said to be continuous on U if it is continuous at each point in U
Finish this definition.
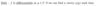
What is v(a) a generalisation of?
df/dx in 1-dimension
If v exists prove it is equal to _∇_f.
What is the theorem that links partial derivatives and differentiabilty?
Let f:U ➝ ℝ be a function on an open set U⊂ℝn, and suppose a ∈ U. If all partial derivativs of f exist and are continuous in a neighbourhood of a, then f is differentiable at a.
Define continuously differentiable.
A function is continuously differentiable at a if it and all of its partial derivatives exist and are continuous at a
Define continuously differentiable on an open set U.
A function is continuosuly differentiable on an open set U if it and all of its partial derivatives exist and are continuous on U.
What does the following theorem imply if a function is continuosuly differentiable on an open set? And why is this important?
Let f:U ➝ ℝ be a function on an open set U⊂ℝn, and suppose a ∈ U. If all partial derivativs of f exist and are continuous in a neighbourhood of a, then f is differentiable at a.
It is also differentiable there - important because continuous differentiability is easier to check than differentiability.
What is a smooth fucntion?
A function in which all partial derivatives of all orders exist.
Finish the following theorem.
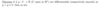
What formula can you use to show something is differentiable?
Where v(a) equals _∇_f
If f(x): U ➝ ℝ is differentiable with U an open set in ℝn, what is the chain rule ?
Define a level set.
A level set S of f:U ➝ ℝ, where U is an open subset of ℝn, is the set of points {x ∈ U : f(x) = c} for some constant c.
What is the level set usually called when n=2?
Level curve
How to do you find a level set when f(x,y) =c?
Set the function equal to c and then rearrange to make y the subject.
Define an explicit function.
y = g(x) gives y an an explicit function of x
Define an implicit funciton.
f(x,y) = 0 gives y as an implicit function of x.
How do you go from an explicit to implicit funciton where g(x) = y?
Set f(x,y) = g(x) - y
What is the implicit function theorem?
What is a critical value?
The point Q on a level curve f = c at which ∇ f = 0, the value of c is called a critical value.
How can’t the level curve be written at a critical value Q?
The level curve cannot be written either as y = g(x) or as x = h(y) in the neighbourhood of Q
Prove
Finish the following.
Prove the following.
What is parametric form for a normal line?
What is the equation for the tangent plane?
Define interior.
A point a ∈ X is in the interior of X, a ∈ int(X) is there is an open ball Bδ(a), for some δ > 0, which is also in X.
Define global maximum.
Define global minimum.
Define strict global maximum.
Define local maximum point.
Define a strict local maximum point.
What is another name for maximum and minimum points?
Extremal points
What are the values taken at maximum and minimum points called?
Extremal values
Local extreme of differentiable fucntions occur at what sort of points?
Critical
Are all critical points local maxima/minima?
Nope
What is a critical point called that is neither a max or min?
Saddle point
Suppose f(x, y) and all partial derivatives up to order n + 1 are continuous in some neighbourhood a. Then for h = (h1, h2) small we have, with a = (x0, y0) what Taylor series expansion do we have for f(a + h)?
What does h.∇ equal in the following?
If a is a critical point what does the following become?
What is H called in the following equation?
The Hessian Matrix
What is the Hessian Matrix?
How do you write the Hessian matrix in index form?
Why is the Hessian symmetric?
Because fxy = fyx
Neglecting higher terms of the taylor expansion what does the following equal?
Why is the sign of hTHh important?
It tells you if the point a is a local maximum or minimum.
What critical point at a do we have if hTHh > 0?
For all small h, a will be a strict local minimum
What critical point do we have if hTH_h_ < 0?
For all small h, a will be strict local maximum
Define positive definite.
Define negative definite.
Define indefinite.
Define positive semi-definite.
Define negative semi-definite.
If H (the hessian matrix) is positive definite what does this say about the point a?
It is a strict local minimum
If H (the hessian matrix) is negative definite what does this say about the point a?
It is a strict lcoal maximum
If H (the hessian matrix) is indefinite what does this say about the point a?
It is a saddle point
What are three tests for positive definiteness?
- Find the eigenvalues of H and refer to the poitns about their values
- H is positive definite if the determinatn of all n of its upper-left sqaure submatrices is positive
- Second derivative test for functions of 2 variables
Which test is the one you should use to test for positive definiteness?
The second derivative test for functions of 2 variables.
Describe the second derivative test for functions of 2 varibales.
What is the theorem about that links global extemum and local extremum.
Define bounded.
What is the extreme value theorem?
What are the four steps to find global extrema of f in a closed and bounded (compact) region X?
What method do you require in the following problem?
Largrange multipliers
Suppose f and g are scalar functions on ℝ2 with continuous partial derivatives and that the contours of f are f(x,y) = d. There is also no critical points of f on the level set g(x,y) = 0 so it is a smooth curve. As we move along g(x,y) = 0 through some point (x0, y0) when is the value of f constant?
- If we are following a contour line of f, i.e. contours of f and g are parallel at (x0,y0)
- f id anyway constant at that point, i.e. _∇_f(x0, y0) = 0
How do you check if you are following a contour line?
What are the solutions at a = (x0, y0) if you are following a contout line of f?
What is λ known as?
The Lagrange multiplier
How can you rewrite the following by introducing the Lagrangian?
What is the equation for the Lagrangian?
How could you find the max and min values of a function on a curve?
Define the Lagrangian, then use simultaneous equations to find an a such that _∇_fL(a) = 0
