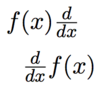Review of Partial Differentation

Question 1

Define the derivative as a limit.

Answer 1

If f(x) is a real-valued function of a single real variable x, then its derivative wrt x is defined as

Question 2

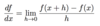
Define the partial derivative w.r.t x as a limit.

Answer 2

If f(x,y) is a real-valued function of two real variables x & y then we define the partial derivatives as

Question 3

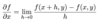
What notation can you use to show what is being held constant during partial differentiation?

Answer 3

Question 4

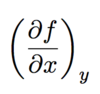
Why does

Answer 4

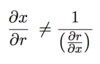
Because different variables are kept constant

Question 5

What is another way to write

Answer 5

Question 6

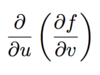
What is the chain rule for

F(t) = f(x(t), y(t))

Answer 6

Question 7

What is the chain rule for

F(t) = f(x(t))

Answer 7

Question 8

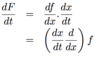
What is the chain rule for the partial derivative of

F(u,v) = f(x(u,v), y(u,v))

Answer 8

Question 9

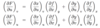
If u and v can be written as functions of x & y, then what are the partial derivatives of

f(x, y) = F(u(x, y), v(x, y))

Answer 9

Question 10

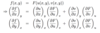
What is the difference between the following:

Answer 10