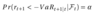VaR Flashcards
What does the Risk-Metrics formula look like?
State a general parametric Conditional VaR model
Which distributions can be used for parametric conditional VaR?
Distributions from the ‘location-scale’ family, such as Student’s T and Normal
What are the steps to implement Filtered Historical Simulation?
1) Demean and devolatilze returns (e.g. compute standardized residuals) 2) Sort and chose alpha*Nth smallest observation 3) Rescale with volatility forecast and add conditional mean
Discuss Pros and Cons of Filtered Historical Simulation
Pros: Few distributional assumptions GARCH advantages Quantile converges to true quantile Cons: Only location scale families to incorporate conditional information Slow convergence
Describe Weighted Historical Simulation
What is a key benefit of Weighted Historical Simulation
No distributional assumptions while incorporating recent conditioning information
What are ways of calculating Unconditional VaR?
Parametric Estimation - Fully parametric mean model with constant variance. Estimate model with MLE Non-parametric (historical simulation) - Empirical distribution of raw returns - Can be smoothed Parametric Monte Carlo - Estimate model for conditional mean and variance - Simulate model for many periods (enough so you don’t need smoothing) - Use simulated distribution - Can give you fat tails because of time-varying volatility - Depends on parameter estimation (bad)
What are 3 ways of evaluating forecasts?
1) Standard Generalized Mincer-Zarnowitz (regress hit on past hits and VaR; HITS should be unforecastable and have mean 0 or alpha according to specification) 2) Likelihood based testing (exploiting Bernoulli characteristics) 3) Probit/Logit (alternative structure to 1) )
What complicates density forecasting?
2+ step ahead forecasts are complicated since variance is stochastic. Even if returns are conditionally normal, we get a variance-mixture of normals, which is not normal. We must ‘integrate out’ the uncertainty in the future variance to determine the future distribution
What is a fan plot?
A plot illustrating density forecasts X-axis number of steps a ahead Y-axis are variable values Darkness indicates density
What is a QQ plot?
Plots of observed values against distribution, matched on quantiles Uses demeaned and devolatilzed observations
Show the steps to perform an LR test on a VaR model
Estimate alpha as HITS/total observations Compute likelihood under estimated alpha and true alpha Test stat: 2*(diff in loglikelihood with estimated and true alpha) is distributed chi^2 with 1 df. Remember that in the test, the log likelihood uses all the observations (sums of individual log density)
What is the Berkowitz test?
It transforms data to uniform (using the assumed CDF) and then transform into std. normal (using inverse std normal) Tests for standard normality by running an AR(1) or higher regression, hypothesizing slope and intercept is zero and variance is one. Tests with maximum likelihood (chi^2 w 3 dfs)
Define Expected Shortfall
Et [r_(t+1) | r_(t+1) < -VaR_(t+1)]
What are the conditions for a coherent risk-measure?
1) Drift invariance 2) Homogeneity 3) Monotonicity 4) Subadditivity
Are VaR and ES coherent risk measures?
VaR is not, ES is. Sometimes violates subadditivity. Can construct to portfolios, the sum of which have larger risk than the sum of the parts
Define Drift Invariance
If adding a constant to the return, the risk measure must decline by this sum
Define monotonicity
If p1 first-order stochastically dominates P2, the risk of p1 must be lower than that of p2
Define first-order stochastic dominance
If p1 is higher than p2 in all possible states of the world, p1 FOSD p2
Define value at risk?
Value at risk satisfies: Pr ( R_t < - VaR_t ) = alpha
What is the difference between risk-metrics and any general GARCH-based parametric VaR model?
In RiskMetrics, the vol. intercept is zero, alpha and beta sum to 1 and returns are assumed to be conditionally normally distributed. Also mean is assumed to be zero
What are some ways of evaluating density forecasts?
Informally: Fan Plots QQ plots Formally: Kolmogrov-Smirnov test Berkowitz test
What does the GMZ for VaR look like?
What is the likelihood for a Bernoulli?
Show a LR test for a VaR model
What is a Kolmogrov-Smirnov test?
How do you perform a probit/logit test on a VaR model
Regressed modified HITs (VAR excedences) on a set of variables transformed through a ‘squash’ function.
The ‘squash’ funciton can be logstic function or Normal CDF. The variables are intercept, VaR and past HITS. Only intercept should be non-zero if model is correcrly specified. Intercept should be inverse squash function of alpha.
What is variance of a Bernoulli?
p(1-p)
What is the general formula for a t-test?
(Estimate - null_value) / standard error
What is the formula for SE?
sqrt(1/(T-1)) * sqrtr(var(parameter))
How do CaViaR models differ from GARCH based VaR models?
They model the quantile directly
CaViaR is hard to optimize since the objective function (tick-loss) is not differentiable, GARCH models are typically done with ML or QML
CaViaR sometimes, thought not always, uses HITs as regressor
When does Weighted Historical Simulation Converge to Historical Simulation?
When the lambda parameter is set to 1, making the weights equal
What is 5% quantile of the std. normal distribution?
-1.645
How to Calculate absolute (not return) variance at risk, knowing portfolio value and distribution?
Value * (-mean + 1.645 * std. dev.)
How to go from monthly to annualized volatility
sqrt(12) * monthly volatility
What are the conditions for an ARCH to be covariance stationary?
Omega (intercept) must be positive
Alphas cannot be negative (for variance to always to be positive)
Also, the sum of alphas must be less than 1, for long-run variance to not be either undefined or negative
What are the conditions for a GARCH to be covariance stationary?
Omega must be positive
Alphas and betas must non-negative
Sum of alphas and betas cannot exceed 1
Show that an ARCH(1) is a AR(1)
Show that a GARCH(1,1) is an ARMA(1,1)
What is the log likelihood of a Bernoulli?
HIT*log(p) + (1-HIT) log(1-p)
Define conditional VaR
What is the null in Granger causality test?
That there is no Granger Causality
What is weak exogeneity?
When there is no Granger causality and errors are uncorrelated
