Topics 52-57

Question 1

VaR conversion to a different time period of time and to a different confidence level

Answer 1

VaR, as calculated previously, measured the risk of a loss in asset value over a short time period. Risk managers may, however, be interested in measuring risk over longer time periods, such as a month, quarter, or year. VaR can be converted from a 1-day basis to a longer basis by multiplying the daily VaR by the square root of the number of days (J) in the longer time period (called the square root rule).

For example, to convert to a weekly VaR, multiply the daily VaR by the square root of 5 (i.e., five business days in a week).

VaR can also be converted to different confidence levels. For example, a risk manager may want to convert VaR with a 95% confidence level to VaR with a 99% confidence level. This conversion is done by adjusting the current VaR measure by the ratio of the updated confidence level to the current confidence level.

We can generalize the conversion method as follows:

Question 2

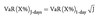
The VaR Methods

Answer 2

The three main VaR methods can be divided into two groups: linear methods and full valuation methods.

1. Linear methods replace portfolio positions with linear exposures on the appropriate risk factor. For example, the linear exposure used for option positions would be delta while the linear exposure for bond positions would be duration. This method is used when calculating VaR with the delta-normal method.
   The delta-normal method is appropriate for large portfolios without significant option-like exposures. This method is fast and efficient.
2. Full valuation methods fully reprice the portfolio for each scenario encountered over a historical period, or over a great number of hypothetical scenarios developed through historical simulation or Monte Carlo simulation. Computing VaR using full revaluation is more complex than linear methods. However, this approach will generally lead to more accurate estimates of risk in the long run.
   Full-valuation methods, either based on historical data or on Monte Carlo simulations, are more time consuming and costly. However, they may be the only appropriate methods for large portfolios with substantial option-like exposures, a wider range of risk factors, or a longer-term horizon.

Question 3

Linear Valuation: The Delta-Normal Valuation Method

Answer 3

The delta-normal approach begins by valuing the portfolio at an initial point as a
relationship to a specific risk factor, S (consider only one risk factor exists):

V₀ = V(S₀)

Here, Δ₀ is the sensitivity of the portfolio to changes in the risk factor, S. As with any linear relationship, the biggest change in the value of the portfolio will accompany the biggest change in the risk factor. The VaR at a given level of significance, z, can be written as:

VaR = |Δ₀| x (zσS₀)

where:

• zσS₀ = VaR_s

_​Generally speaking, VaR developed by a delta-normal method is more accurate over shorter horizons than longer horizons.

Since the delta-normal method is only accurate for linear exposures, non-linear exposures, such as convexity, are not adequately captured with this VaR method. By using a Taylor series expansion, convexity can be accounted for in a fixed income portfolio by using what is known as the delta-gamma method.

The delta-normal method (a.k.a. the variance-covariance method or the analytical method) for estimating VaR requires the assumption of a normal distribution.

The assumption of normality is troublesome because many assets exhibit skewed return distributions (e.g., options), and equity returns frequently exhibit leptokurtosis (fat tails). When a distribution has “fat tails,” VaR will tend to underestimate the loss and its associated probability. Also know that delta-normal VaR is calculated using the historical standard deviation, which may not be appropriate if the composition of the portfolio changes, if the estimation period contained unusual events, or if economic conditions have changed.

Advantages of the delta-normal VaR method include the following:

• Easy to implement.
• Calculations can be performed quickly.
• Conducive to analysis because risk factors, correlations, and volatilities are identified.

Disadvantages of the delta-normal method include the following:

• The need to assume a normal distribution.
• The method is unable to properly account for distributions with fat tails, either because of unidentified time variation in risk or unidentified risk factors and/or correlations.
• Nonlinear relationships of option-like positions are not adequately described by the delta-normal method. VaR is misstated because the instability of the option deltas is not captured.

Question 4

Converting annual standard deviation into daily and monthly standard deviation

Answer 4

Question 5

Historical Simulation Method: advantages and disadvantages

Answer 5

Advantages of the historical simulation method include the following:

• The model is easy to implement when historical data is readily available.
• Calculations are simple and can be performed quickly.
• Horizon is a positive choice based on the intervals of historical data used.
• Full valuation of portfolio is based on actual prices.
• It is not exposed to model risk.
• It includes all correlations as embedded in market price changes.

Disadvantages of the historical simulation method include the following:

• It may not be enough historical data for all assets.
• Only one path of events is used (the actual history), which includes changes in correlations and volatilities that may have occurred only in that historical period.
• Time variation of risk in the past may not represent variation in the future.
• The model may not recognize changes in volatility and correlations from structural changes.
• It is slow to adapt to new volatilities and correlations as old data carries the same weight as more recent data. However, exponentially weighted average (EWMA) models can be used to weigh recent observations more heavily.
• A small number of actual observations may lead to insufficiently defined distribution tails.

Question 6

Monte Carlo Simulation Method: advantages and disadvantages

Answer 6

Advantages of the Monte Carlo method include the following:

• It is the most powerful model.
• It can account for both linear and nonlinear risks.
• It can include time variation in risk and correlations by aging positions over chosen horizons.
• It is extremely flexible and can incorporate additional risk factors easily.
• Nearly unlimited numbers of scenarios can produce well-described distributions.

Disadvantages of the Monte Carlo method include the following:

• There is a lengthy computation time as the number of valuations escalates quickly.
• It is expensive because of the intellectual and technological skills required.
• It is subject to model risk of the stochastic processes chosen.
• It is subject to sampling variation at lower numbers of simulations.

Question 7

Explain how asset return distributions tend to deviate from the normal distribution

Answer 7

Three common deviations from normality that are problematic in modeling risk result from asset returns that are: fat-tailed, skewed, or unstable.

Fat-tailed refers to a distribution with a higher probability of observations occurring in the tails relative to the normal distribution.

In modeling risk, a number of assumptions are necessary. If the parameters of the model are unstable, they are not constant but vary over time. For example, if interest rates, inflation, and market premiums are changing over time, this will affect the volatility of the returns going forward.

Question 8

Explain reasons for fat tails in a return distribution and describe their imphcations. Distinguish between conditional and unconditional distributions.

Answer 8

The phenomenon of “fat tails” is most likely the result of the volatility and/or the mean of the distribution changing over time. If the mean and standard deviation are the same for asset returns for any given day, the distribution of returns is referred to as an unconditional distribution of asset returns. However, different market or economic conditions may cause the mean and variance of the return distribution to change over time. In such cases, the return distribution is referred to as a conditional distribution.

Assume we separate the full data sample into two normally distributed subsets based on market environment with conditional means and variances. Pulling a data sample at different points of time from the full sample could generate fat tails in the unconditional distribution even if the conditional distributions are normally distributed with similar means but different volatilities. If markets are efficient and all available information is reflected in stock prices, it is not likely that the first moments or conditional means of the distribution vary enough to make a difference over time.

The second possible explanation for “fat tails” is that the second moment or volatility is time-varying. This explanation is much more likely given observed changes in interest rate volatility (e.g., prior to a much-anticipated Federal Reserve announcement). Increased market uncertainty following significant political or economic events results in increased volatility of return distributions.

Question 9

Describe the implications of regime switching on quantifying volatility

Answer 9

A regime-switching volatility model assumes different market regimes exist with high or low volatility. The conditional distributions of returns are always normal with a constant mean but either have a high or low volatility.

The probability of large deviations from normality occurring are much less likely under the regime-switching model. The regime-switching model captures the conditional normality and may resolve the fat-tail problem and other deviations from normality.

If we assume that volatility varies with time and that asset returns are conditionally normally distributed, then we may be able to tolerate the fat-tail issue.

However, some tools exist that serve to complement VaR by examining the data in the tail of the distribution. For example, stress testing and scenario analysis can examine extreme events by testing how hypothetical and/or past financial shocks will impact VaR. Also, extreme value theory (EVT) can be applied to examine just the tail of the distribution and some classes of EVT apply a separate distribution to the tail. Despite not being able to accurately capture events in the tail, VaR is still useful for approximating the risk level inherent in financial assets.

Question 10

Explain the various approaches for estimating VaR

Answer 10

A value at risk (VaR) method for estimating risk is typically either a historical-based approach or an implied-volatility-based approach. Under the historical-based approach, the shape of the conditional distribution is estimated based on historical time series data.

Historical-based approaches typically fall into three sub-categories: parametric,
nonparametric, and hybrid.

1. The parametric approach requires specific assumptions regarding the asset returns distribution. A parametric model typically assumes asset returns are normally or lognormally distributed with time-varying volatility. The most common example of the parametric method in estimating future volatility is based on calculating historical variance or standard deviation using “mean squared deviation.” For example, the following equation is used to estimate future variance based on a window of the K most recent returns data (in order to adjust for one degree of freedom related to the conditional mean, the denominator in the formula is K — 1. In practice, adjusting for the degrees of freedom makes little difference when large sample sizes are used).
2. The nonparametric approach is less restrictive in that there are no underlying assumptions of the asset returns distribution. The most common nonparametric approach models volatility using the historical simulation method.
3. As the name suggests, the hybrid approach combines techniques of both parametric and nonparametric methods to estimate volatility using historical data.

The implied-volatility-based approach uses derivative pricing models such as the Black-Scholes-Merton option pricing model to estimate an implied volatility based on current market data rather than historical data.

The delta-normal method is an example of a parametric approach.

Question 11

Parametric Approaches for VaR

Answer 11

The RiskMetrics® [i.e., exponentially weighted moving average (EWMA) model] and GARCH approaches are both exponential smoothing weighting methods. RiskMetrics® is actually a special case of the GARCH approach. Both exponential smoothing methods are similar to the historical standard deviation approach because all three methods:

• Are parametric.
• Attempt to estimate conditional volatility.
• Use recent historical data.
• Apply a set of weights to past squared returns.

The RiskMetrics® approach is just an EWMA model that uses a pre-specified decay factor for daily data (0.94) and monthly data (0.97).

The only major difference between the historical standard deviation approach and the two exponential smoothing approaches is with respect to the weights placed on historical returns that are used to estimate future volatility. The historical standard deviation approach assumes all K returns in the window are equally weighted. Conversely, the exponential smoothing methods place a higher weight on more recent data, and the weights decline exponentially to zero as returns become older. The rate at which the weights change, or smoothness, is determined by a parameter λ (known as the decay factor) raised to a power. The parameter λ must fall between 0 and 1 (i.e., 0 < λ < 1); however, most models use
parameter estimates between 0.9 and 1 (i.e., 0.9 < λ < 1).

Figure 4 illustrates the weights of the historical volatility for the historical standard
deviation approach and RiskMetrics® approach. Using the RiskMetrics® approach,
conditional variance is estimated using the following formula:

Question 12

Using the RiskMetrics® approach, calculate the weight for the most current historical return, t = 0, when X = 0.97.

Calculate the weight for the most recent return using historical standard deviation approach with K = 75.

Answer 12

The weight for the most current historical return, t = 0, when λ = 0.97 is calculated as follows:
(1 - λ) λ^t = (1 - 0.97)0.97⁰ = 0.03

All historical returns are equally weighted. Therefore, the weights will all be equal to
0.0133 (i.e., 1 / K = 1 / 75 = 0.0133).

Question 13

GARCH

Answer 13

Question 14

Nonparametric vs. Parametric VaR Methods

Answer 14

Three common types of nonparametric methods used to estimate VaR are:

1. historical simulation,
2. multivariate density estimation, and
3. hybrid.

These nonparametric methods exhibit the following advantages and disadvantages over parametric approaches.

Advantages of nonparametric methods compared to parametric methods:

• Nonparametric models do not require assumptions regarding the entire distribution of returns to estimate VaR.
• Fat tails, skewness, and other deviations from some assumed distribution are no longer a concern in the estimation process for nonparametric methods.
• Multivariate density estimation (MDE) allows for weights to vary based on how relevant the data is to the current market environment, regardless of the timing of the most relevant data.
• MDE is very flexible in introducing dependence on economic variables (called state variables or conditioning variables).
• Hybrid approach does not require distribution assumptions because it uses a historical simulation approach with an exponential weighting scheme.

Disadvantages of nonparametric methods compared to parametric methods:

• Data is used more efficiently with parametric methods than nonparametric methods. Therefore, large sample sizes are required to precisely estimate volatility using historical simulation.
• Separating the full sample of data into different market regimes reduces the amount of usable data for historical simulations.
• MDE may lead to data snooping or over-fitting in identifying required assumptions regarding the weighting scheme identification of relevant conditioning variables and the number of observations used to estimate volatility.
• MDE requires a large amount of data that is directly related to the number of conditioning variables used in the model

Question 15

Hybrid Approach

Answer 15

Question 16

Multivariate Density Estimation (MDE)

Answer 16

Question 17

Explain the process of return aggregation in the context of volatility forecasting methods

Answer 17

When a portfolio is comprised of more than one position using the RiskMetrics® or historical standard deviation approaches, a single VaR measurement can be estimated by assuming asset returns are all normally distributed. The covariance matrix of asset returns is used to calculate portfolio volatility and VaR. The delta-normal method requires the calculation of N variances and [N x (N — 1)]/2 covariances for a portfolio of Appositions. The model is subject to estimation error due to the large number of calculations. In addition, some markets are more highly correlated in a downward market, and in such cases, VaR is underestimated.

The historical simulation approach requires an additional step that aggregates each period’s historical returns weighted according to the relative size of each position. The weights are based on the market value of the portfolio positions today, regardless of the atual allocation of positions K days ago in the estimation window. A major advantage of this approach compared to the delta-normal approach is that no parameter estimates are required.Therefore, the model is not subject to estimation error related to correlations and the problem of higher correlations in downward markets.

A third approach to calculating VaR estimates the volatility of the vector of aggregated returns and assumes normality based on the strong law of large numbers. The strong law of large numbers states that an average of a very large number of random variables will end up converging to a normal random variable. However, this approach can only be used in a well-diversified portfolio.

Question 18

Evaluate implied volatility as a predictor of future volatility and its shortcomings

Answer 18

Estimating future volatility using historical data requires time to adjust to current changes in the market. An alternative method for estimating future volatility is implied volatility. The Black-Scholes-Merton model is used to infer an implied volatility from equity option prices. Using the most liquid at-the-money put and call options, an average implied volatility is extrapolated using the Black-Scholes-Merton model.

A big advantage of implied volatility is the forward-looking predictive nature of the model. Forecast models based on historical data require time to adjust to market events. The implied volatility model reacts immediately to changing market conditions.

The implied volatility model does, however, exhibit some disadvantages. The biggest disadvantage is that implied volatility is model dependent. A major assumption of the model is that asset returns follow a continuous time lognormal diffusion process. The volatility parameter is assumed to be constant from the present time to the contract maturity date. However, implied volatility varies through time; therefore, the Black-Scholes-Merton model is misspecified. Options are traded on the volatility of the underlying asset with what is known as “vol” terms. In addition, at a given point in time, options with the same underlying assets may be trading at different vols. Empirical results suggest implied volatility is on average greater than realized volatility. In addition to this upward bias in implied volatility, there is the problem that available data is limited to only a few assets and market factors.

Question 19

Explain long horizon volatility/VaR and the process of mean reversion according to an AR(1) model. Calculate conditional volatility with and without mean reversion.

Answer 19

To demonstrate mean reversion, consider a time series model with one lagged variable:

X_i = a + b x X_i-1

This type of regression, with a lag of its own variable, is known as an autoregressive (AR) model. In this case, since there is only one lag, it is referred to as an AR(1) model. The longrun mean of this model is evaluated as [a / (1 — b)]. The key parameter in this long-run mean equation is b. Notice that if b = 1, the long-run mean is infinite (i.e., the process is a random walk). If b, however, is less than 1, then the process is mean reverting (i.e., the time series will trend toward its long-run mean).

Question 20

Backtesting VaR model

Answer 20

Backtesting is the process of comparing losses predicted by the value at risk (VaR) model to those actually experienced over the sample testing period. If a model were completely accurate, we would expect VaR to be exceeded (this is called an exception) with the same frequency predicted by the confidence level used in the VaR model. In other words, the probability of observing a loss amount greater than VaR is equal to the significance level (x%). This value is also obtained by calculating one minus the confidence level.

For example, if a VaR of $10 million is calculated at a 95% confidence level, we expect to have exceptions (losses exceeding $10 million) 5% of the time. If exceptions are occurring with greater frequency, we may be underestimating the actual risk. If exceptions are occurring less frequently, we may be overestimating risk.

There are three desirable attributes of VaR estimates that can be evaluated when using a backtesting approach. The first desirable attribute is that the VaR estimate should be unbiased. To test this property, we use an indicator variable to record the number of times an exception occurs during a sample period. For each sample return, this indicator variable is recorded as 1 for an exception or 0 for a non-exception. The average of all indicator variables over the sample period should equal x% (i.e., the significance level) for the VaR estimate to be unbiased.

A second desirable attribute is that the VaR estimate is adaptable. For example, if a large return increases the size of the tail of the return distribution, the VaR amount should also be increased. Given a large loss amount, VaR must be adjusted so that the probability of the next large loss amount again equals x%. This suggests that the indicator variables, discussed previously, should be independent of each other. It is necessary that the VaR estimate account for new information in the face of increasing volatility.

A third desirable attribute, which is closely related to the first two attributes, is for the VaR estimate to be robust. A strong VaR estimate produces only a small deviation between the number of expected exceptions during the sample period and the actual number of exceptions. This attribute is measured by examining the statistical significance of the autocorrelation of extreme events over the backtesting period. A statistically significant autocorrelation would indicate a less reliable VaR measure.

By examining historical return data, we can gain some clarity regarding which VaR method actually produces a more reliable estimate in practice. In general, VaR approaches that are nonparametric (e.g., historical simulation and the hybrid approach) do a better job at producing VaR amounts that mimic actual observations when compared to parametric methods such as an exponential smoothing approach (e.g., GARCH). The likely reason for this performance difference is that nonparametric approaches can more easily account for the presence of fat tails in a return distribution. Note that higher levels of λ (the exponential weighing parameter) in the hybrid approach will perform better than lower levels of λ. Finally, when testing the autocorrelation of tail events, we find that the hybrid approach performs better than exponential smoothing approaches. In other words, the hybrid approach tends to reject the null hypothesis that autocorrelation is equal to zero fewer times than exponential smoothing approaches.

Question 21

Describe and calculate VaR for linear derivatives

Answer 21

In general, the VaR of a long position in a linear derivative is VaR_p = ΔVaR_f, where
VaR_f is the VaR of the underlying factor and the derivative’s delta, Δ, is the sensitivity of the derivative’s price to changes in the underlying factor.

Question 22

Taylor Series approximation of the function f(x)

Answer 22

Question 23

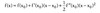
Explain the full revaluation method for computing VaR. Compare delta-normal and full revaluation approaches for computing VaR

Answer 23

Question 24

Explain structured Monte Carlo method for computing VaR and identify strengths and weaknesses of this approach

Answer 24

The structured Monte Carlo (SMC) approach simulates thousands of valuation outcomes for the underlying assets based on the assumption of normality.

An advantage of the SMC approach is that it is able to address multiple risk factors by assuming an underlying distribution and modeling the correlations among the risk factors.

A disadvantage of the SMC approach is that in some cases it may not produce an accurate forecast of future volatility and increasing the number of simulations will not improve the forecast.

Question 25

Describe the implications of correlation breakdown for scenario analysis

Answer 25

The key point here is that in times of crisis, correlations increase (some substantially) and strategies that rely on low correlations fall apart in those times. Certain economic or crisis events can cause diversification benefits to deteriorate in times when the benefits are most needed.

A simulation using the SMC approach is not capable of predicting scenarios during times of crisis if the covariance matrix was estimated during normal times.

Question 26

Stress testing

Answer 26

Stressing the correlation is a method used to model the contagion effect that could occur in a crisis event.

One approach for stress testing is to examine historical crisis events, such as the Asian crisis, October 1987 market crash, etc. After the crisis is identified, the impact on the current portfolio is determined. The advantage of this approach is that no assumptions of underlying asset returns or normality are needed. The biggest disadvantage of using historical events for stress testing is that it is limited to only evaluating events that have actually occurred.

The historical simulation approach does not limit the analysis to specific events. Under this approach, the entire data sample is used to identify “extreme stress” situations for different asset classes. For example, certain historical events may impact the stock market more than the bond market. The objective is to identify the five to ten worst weeks for specific asset classes and then evaluate the impact on today’s portfolio. The advantage of this approach is that it may identify a crisis event that was previously overlooked for a specific asset class. The focus is on identifying extreme changes in valuation instead of extreme movements in
underlying risk factors. The disadvantage of the historical simulation approach is that it is still limited to actual historical data.

An alternative approach is to analyze different predetermined stress scenarios.

An advantage to scenario analysis is that it is not limited to the evaluation of risks that have occurred historically. It can be used to address any possible scenarios. A disadvantage of the stress scenario approach is that the risk measure is deceptive for various reasons. For example, a shift in the domestic yield curve could cause estimation errors by overstating the risk for a long and short position and understating the risk for a long-only position.

Question 27

Describe worst-case scenario (WCS) analysis and compare WCS to VaR

Answer 27

The worst case scenario (WCS) assumes that an unfavorable event will occur with certainty. The focus is on the distribution of worst possible outcomes given an unfavorable event. An expected loss is then determined from this worst case distribution analysis. Thus, the WCS information extends the VaR analysis by estimating the extent of the loss given an unfavorable event occurs.

In other words, the tail of the original return distribution is more thoroughly examined with another distribution that includes only probable extreme events. For example, within the lowest 5% of returns, another distribution can be formed with just those returns and a 1 % WCS return can then be determined. Recall that VaR provides a value of the minimum loss for a given percentage, but says nothing about the severity of the losses in the tail. WCS analysis attempts to complement the VaR measure with analysis of returns in the tail.

Question 28

Describe the mean-variance framework and the efficient frontier

Answer 28

Under the mean-variance framework, it is necessary to assume that return distributions for portfolios are elliptical distributions. The most commonly known elliptical probability distribution function is the normal distribution.

Question 29

Market portfolio

Answer 29

If we now assume that there is a risk-free security, then the mean-variance framework is extended beyond the efficient frontier. Figure 2 illustrates that the optimal set of portfolios now lie on a straight line that runs from the risk-free security through the market portfolio, M. All investors will now seek investments by holding some portion of the risk-free security and the market portfolio. To achieve points on the line to the right of the market portfolio, an investor who is very aggressive will borrow money (at the risk-free rate) and invest in more of the market portfolio. More risk-averse investors will hold some combination of the risk-free security and the market portfolio to achieve portfolios on the line segment between the risk-free security and the market portfolio.

Question 30

Role of mean in estimating how VaR changes with changes in the holding period

Answer 30

The rate at which VaR increases is determined in part by the mean of the distribution.

• If the return distribution has a mean, μ, equal to 0, then VaR rises with the square root of the holding period (i.e., the square root of time).
• If the return distribution has a μ > 0, then VaR rises at a lower rate and will eventually decrease.

Thus, the mean of the distribution is an important determinant for estimating how VaR changes with changes in the holding period.

Question 31

Limitations of VaR

Answer 31

VaR estimates are subject to both model risk and implementation risk. Model risk is the risk of errors resulting from incorrect assumptions used in the model. Implementation risk is the risk of errors resulting from the implementation of the model.

Another major limitation of the VaR measure is that it does not tell the investor the amount or magnitude of the actual loss.

To summarize, VaR measurements work well with elliptical return distributions, such as the normal distribution. VaR is also able to calculate the risk for non-normal distributions; however, VaR estimates may be unreliable in this case. Limitations in implementing the VaR model for determining risk result from the underlying return distribution, arbitrary confidence level, arbitrary holding period, and the inability to calculate the magnitude of losses. The measure of VaR also violates the coherent risk measure property of subadditivity when the return distribution is not elliptical.

Question 32

Define the properties of a coherent risk measure. Explain why VaR is not a coherent risk measure

Answer 32

Subadditivity, the most important property for a coherent risk measure, states that a portfolio made up of sub-portfolios will have equal or less risk than the sum of the risks of each individual sub-portfolio. VaR violates the property of subadditivity.

Question 33

Explain and calculate expected shortfall (ES), and compare and contrast VaR and ES.

Answer 33

Expected shortfall (ES) is the expected loss given that the portfolio return already lies below the pre-specified worst case quantile return (i.e., below the 5th percentile return). In other words, expected shortfall is the mean percent loss among the returns falling below the q-quantile. Expected shortfall is also known as conditional VaR or expected tail loss (ETL).

ES is a more appropriate risk measure than VaR for the following reasons:

• ES satisfies all of the properties of coherent risk measurements including subadditivity. VaR only satisfies these properties for normal distributions.
• The portfolio risk surface for ES is convex because the property of subadditivity is met. Thus, ES is more appropriate for solving portfolio optimization problems than the VaR method.
• ES gives an estimate of the magnitude of a loss for unfavorable events. VaR provides no estimate of how large a loss may be.
• ES has less restrictive assumptions regarding risk/return decision rules.

Question 34

Describe spectral risk measures, and explain how VaR and ES are special cases of spectral risk measures

Answer 34

A more general risk measure than either VaR or ES is known as the risk spectrum or risk aversion function. The risk spectrum measures the weighted averages of the return quantiles from the loss distributions. ES is a special case of this risk spectrum measure. When modeling the ES case, the weighting function is set to [1 / (1 — confidence level)] for tail losses. All other quantiles will have a weight of zero.

VaR is also a special case of spectral risk measure models.

Question 35

Describe how the results of scenario analysis can be interpreted as coherent risk measures

Answer 35

The outcomes of scenario analysis are coherent risk measurements, because expected shortfall is a coherent risk measurement.

The ES for the distribution can be computed by finding the arithmetic average of the losses for various scenario loss outcomes.

Question 36

Hedge ratio for long call option (in one-period binominal tree)

Answer 36

The hedge ratio tells us how many units of the stock are to be shorted per long call option to make the hedge work. In the single-period model, the hedge ratio may be calculated as follows:

HR = (c_U - c_D) / (S_U - S_D)

Question 37

Synthetic Call Replication

Answer 37

Question 38

Risk-Neutral Valuation (probabilities of upward and downward movements)

Answer 38

Question 39

Describe how volatility is captured in the binomial model

Answer 39

Notice that a high standard deviation will result in a large difference between the stock price in an up state, S_U, and the stock price in a down state, S_D. If the standard deviation were zero, the binomial tree would collapse into a straight line and S_U would equal S_D.

Obviously, the higher the standard deviation, the greater the
dispersion between stock prices in up and down states. Therefore volatility, as measured here by standard deviation, can be captured by evaluating stock prices at each time period considered in the tree.

Question 40

Explain how the binomial model can be altered to price options on: stocks with dividends, stock indices, currencies, and futures

Answer 40

Question 41

Valuation of American options using binominal model

Answer 41

Valuing American options with a binomial model requires the consideration of the ability of the holder to exercise early. In the case of a two-step model, that means determining whether early exercise is optimal at the end of the first period. If the payoff from early exercise (the intrinsic value of the option) is greater than the option’s value (the present value of the expected payoff at the end of the second period), then it is optimal to exercise early.

When evaluating American options, you need to assess early exercise at each node in the tree. This includes the initial node (node 0). If the option price today (calculated via the binomial model) is less than the value of early exercise today, then the option should be exercised early.

Question 42

Describe how the value calculated using a binomial model converges as time periods are added

Answer 42

If we shorten the length of the intervals in a binomial model, there are more intervals over the same time period, more branches to consider, and more possible ending values. If we continue to shrink the length of intervals in the model until they are what mathematicians call “arbitrarily small,” we approach continuous time as the limiting case of the binomial model. The model for option valuation in the next topic (the Black-Scholes-Merton model) is a continuous time model. The binomial model “converges” to this continuous time model as we make the time periods arbitrarily small.

Question 43

Explain the lognormal property of stock prices

Answer 43

Question 44

Compute the realized return and historical volatility of a stock

Answer 44

Question 45

Expected stock price using BSM model

Answer 45

Question 46

Describe the assumptions underlying the Black-Scholes-Merton option pricing model

Answer 46

In addition to the no-arbitrage condition, the assumptions underlying the BSM model are the following:

• The price of the underlying asset follows a lognormal distribution. A variable that is lognormally distributed is one where the logs of the values (in this case, the continuous returns) are normally distributed. It has a minimum of zero and conforms to prices better than the normal distribution (which would produce negative prices).
• The (continuous) risk-free rate is constant and known.
• The volatility of the underlying asset is constant and known. Option values depend on the volatility of the price of the underlying asset or interest rate.
• Markets are “frictionless.” There are no taxes, no transactions costs, and no restrictions on short sales or the use of short-sale proceeds.
• The underlying asset has no cash flow, such as dividends or coupon payments.
• The options valued are European options, which can only be exercised at maturity. The model does not correctly price American options.

Question 47

Compute the value of a European option using the Black-Scholes-Merton model on a non-dividend-paying stock

Answer 47

Question 48

Compute the value of a European option using the Black-Scholes-Merton model on a dividend-paying stock

Answer 48

Just as we subtracted the present value of expected cash flows from the asset price when valuing forwards and futures, we can subtract it from the asset price in the BSM model. Since the BSM model is in continuous time, in practice S₀e^-qT is substituted for S₀ in the BSM formula, where q is equal to the continuously compounded rate of dividend payment. Over time, the asset price is discounted by a greater amount to account for the greater amount of cash flows. Cash flows will increase put values and decrease call values.

Question 49

Explain how dividends affect the decision to exercise early for American call and put options

Answer 49

Question 50

Compute the value of a warrant and identify the complications involving the valuation of warrants

Answer 50

Warrants are attachments to a bond issue that give the holder the right to purchase shares of a security at a stated price. After purchasing the bond, warrants can be exercised separately or stripped from the bond and sold to other investors. Hence, warrants can be valued as a separate call option on the firm’s shares.

One distinction is necessary, though. With call options, the shares are already outstanding, and the exercise of a call option triggers the trading of shares among investors at the strike price of the call options. When an investor exercises warrants, the investor purchases shares directly from the firm.

Question 51

Define implied volatilities and describe how to compute implied volatilities from market prices of options using the Black-Scholes-Merton model

Answer 51

Notice in call and put equations that volatility is unobservable. Historical data can serve as a basis for what volatility might be going forward, but it is not always representative of the current market. Consequently, practitioners will use the BSM option pricing model along with market prices for options and solve for volatility. The result is what is known as implied volatility.

Question 52

Naked/covered call option position

Answer 52

A naked position occurs when one party sells a call option without owning the underlying asset.

A covered position occurs when the party selling a call option owns the underlying asset.

Question 53

Explain how naked and covered option positions generate a stop loss trading strategy

Answer 53

Stop-loss strategies with call options are designed to limit the losses associated with short option positions (i.e., those taken by call writers). The strategy requires purchasing the underlying asset for a naked call position when the asset rises above the option’s strike price. The asset is then sold as soon as it goes below the strike price. The objective here is to hold a naked position when the option is out-of-the-money and a covered position when the option is in-the-money.

The main drawbacks to this simplistic approach are transaction costs and price uncertainty. The costs of buying and selling the asset can become high as the frequency of stock price fluctuations about the exercise price increases. In addition, there is great uncertainty as to whether the asset will be above (or below) the strike price at expiration.

Question 54

Delta of an option

Answer 54

Question 55

Calculation option delta using BSM

Answer 55

To completely hedge a long stock or short call position, an investor must purchase the number of shares of stock equal to delta times the number of options sold. Another term for being completely hedged is delta-neutral.

Delta can also be calculated as the N(d₁) in the Black-Scholes-Merton option pricing model. Recall from the previous topic that d₁ is equal to:

Question 56

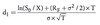
Forward Delta

Answer 56

The delta of a forward position is equal to one, implying a one-to-one relationship between the value of the forward contract and its underlying asset. A forward contract position can easily be hedged with an offsetting underlying asset position with the same number of securities.

Question 57

Futures Delta

Answer 57

Question 58

Number of options needed to delta hedge

Answer 58

Question 59

Describe the dynamic aspects of delta hedging and distinguish between dynamic hedging and hedge-and-forget strategy

Answer 59

A key consideration in delta-neutral hedging is that the delta-neutral position only holds for very small changes in the value o f the underlying stock. Hence, the delta-neutral portfolio must be frequently (continuously) rebalanced to maintain the hedge.

As the delta changes, the number of calls that need to be sold to maintain a risk-free position also changes. Hence, continuously maintaining a delta-neutral position can be very costly in terms of transaction costs associated with either closing out options or selling additional contracts.

Adjusting the hedge on a frequently basis is known as dynamic hedging. If, instead, the hedge is initially set-up but never adjusted, it is referred to as static hedging. This type of hedge is also known as a hedge-andforget strategy.

Question 60

Other Portfolio Hedging Approaches

Answer 60

Question 61

Define the delta of a portfolio

Answer 61

Question 62

Calculating Theta

Answer 62

Question 63

Specific characteristics of theta

Answer 63

Question 64

Gamma calculation

Answer 64

Question 65

Properties of Gamma

Answer 65

• Gamma is largest when an option is at-the-money (at stock price = X). When an option is deep in-the-money or out-of-the-money, changes in stock price have little effect on gamma.
• When gamma is large, delta will be changing rapidly. On the other hand, when gamma is small, delta will be changing slowly. Since gamma represents the curvature component of the call-price function not accounted for by delta, it can be used to minimize the hedging error associated with a linear relationship (delta) to represent the curvature of the call-price function.
• Delta-neutral positions can hedge the portfolio against small changes in stock price, while gamma can help hedge against relatively large changes in stock price. Therefore, it is not only desirable to create a delta-neutral position but also to create one that is gamma-neutral. In that way, neither small nor large stock price changes adversely affect the portfolio’s value.
• The specific relationship that determines the number of options that must be added to an existing portfolio to generate a gamma-neutral position is — (Γ_p / Γ_T), where Γ_p is the gamma of the existing portfolio position, and Γ_T is the gamma of a traded option that can be added.

Question 66

Relationship Among Delta, Theta, and Gamma

Answer 66

Question 67

Vega

Answer 67

Question 68

Rho

Answer 68

Question 69

Describe how hedging activities take place in practice, and describe how scenario analysis can be used to formulate expected gains and losses with option positions

Answer 69

One of the main problems facing options traders is the expense associated with trying to maintain positions that are neutral to the Greeks. Although delta-neutral positions can be created, it is not as easy to find securities at reasonable prices that can mitigate the negative effects associated with gamma and vega.

To make things somewhat more manageable, large financial institutions usually adjust to a delta-neutral position and then monitor exposure to the other Greeks. Two offsetting situations assist in this monitoring activity. First, institutions that have sold options to their clients are exposed to negative gamma and vega, which tend to become more negative as time passes. In contrast, when the options are initially sold at-the-money, the level of sensitivity to gamma and vega is highest, but as time passes, the options tend to go either in-the-money or out-of-the-money. The further in- or out-of-the-money an option becomes, the less the impact of gamma and vega on the delta-neutral position.

Scenario analysis involves calculating expected portfolio gains or losses over desired periods using different inputs for underlying asset price and volatility. In this way, traders can assess the impact of changing various factors individually, or simultaneously, on their overall position.

Question 70

Describe how portfolio insurance can be created through option instruments and stock index futures

Answer 70

Portfolio insurance is the combination of:

1. an underlying instrument and
2. either cash or a derivative that generates a floor value for the portfolio in the event that market values decline, while still allowing for upside potential in the event that market values rise.

The simplest way to create portfolio insurance is to buy put options on an underlying portfolio.

In this case, any loss on the portfolio may be offset with gains on the long put position. Simply buying puts on the underlying portfolio may not be feasible because the put options needed to generate the desired level of portfolio insurance may not be available. As an alternative to buying the puts, a synthetic put position can be created with index futures contracts. This is accomplished by selling index futures contracts in an amount equivalent to the proportion of the portfolio dictated by the delta of the required put option. The main reasons traders may prefer synthetically creating the portfolio insurance position with index futures include substantially lower trading costs and relatively higher levels of liquidity.