Topics 24-30

Question 1

Mean Squared Error and Model Selection

Answer 1

Mean squared error (MSE) is a statistical measure computed as the sum of squared residuals divided by the total number of observations in the sample.

The MSE is based on in-sample data. The regression model with the smallest MSE is also the model with the smallest sum of squared residuals.

MSE is closely related to the coefficient of determination (R²). Notice in the R² equation that the numerator is simply the sum of squared residuals (SSR), which is identical to the MSE numerator.

Model selection is one of the most important criteria in forecasting data. Unfortunately, selecting the best model based on the highest R² or smallest MSE is not effective in producing good out-of-sample forecasting models. A better methodology to select the best forecasting model is to find the model with the smallest out-of-sample, one-step-ahead MSE.

Question 2

The s² Measure, adjusted R²

Answer 2

Question 3

Akaike information criterion (AIC) and the Schwarz information criterion (SIC)

Answer 3

Question 4

Explain the necessary conditions for a model selection criterion to demonstrate consistency

Answer 4

Consistency is a key property that is used to compare different selection criteria.

Two conditions are required for a model selection criteria to be considered consistent based on whether the true model is included among the regression models being considered.

• When the true model or data generating process (DGP) is one of the defined regression models, then the probability of selecting the true model approaches one as the sample size increases.
• When the true model is not one of the defined regression models being considered, then the probability of selecting the best approximation model approaches one as the sample size increases.

The reality is that the second condition of consistency is more relevant. All of our models are most likely false so, therefore, we are seeking the best approximation.

The most consistent selection criteria with the greatest penalty factor for degrees of freedom is the SIC.

While the SIC is considered the most consistent criteria, the AIC is still a useful measure. If we consider the fact that the true model may be much more complicated than the models under consideration, then the AIC measure should be examined. Asymptotic efficiency is the property that chooses a regression model with one-step-ahead forecast error variances closest to the variance of the true model. Interestingly, the AIC is asymptotically efficient and the SIC is not asymptotically efficient.

Note that SIC is consistent only if true model or it’s best approximation is in the set of models being evaluated. This is rarely the case since the true DGP or any of it’s approximations are much more complicated than any of the models that we can fit (and handle). We include another desirable property asymptotic efficiency.

An asymptotically efficient model selection criterion chooses a sequence of models (as sample size grows) whose 1-step-ahead forecast error variance approaches that of the true model (assuming it is known) at a rate that is at least as fast as any other model selection criterion. AIC although being inconsistent, is asymptotically efficient, while SIC is not.

Question 5

Two approaches for modeling and forecasting a time series impacted by seasonality

Answer 5

There are two approaches for modeling and forecasting a time series impacted by seasonality:

1. using a seasonally adjusted time series and
2. regression analysis with seasonal dummy variables.

A seasonally adjusted time series is created by removing the seasonal variation from the data. This type of adjustment is commonly made in macroeconomic forecasting where the goal is to only measure the nonseasonal fluctuations of a variable. However, the use of seasonal adjustments in business forecasting is usually inappropriate because seasonality often accounts for large variations in a time series. Financial forecasters should be interested in capturing all variation in a time series, not just the nonseasonal portions.

Question 6

Explain how to construct an h-step-ahead point forecast

Answer 6

Question 7

Autoregression

Answer 7

Autoregression refers to the process of regressing a variable on lagged or past values of itself. As you will see in the next topic, when the dependent variable for a time series is regressed against one or more lagged values of itself, the resultant model is called as an autoregressive (AR) model. For example, the sales for a firm could be regressed against the sales for the firm in the previous month. Thus, in an autoregressive time series, past values of a variable are used to predict the current (and hence future) value of the variable.

Question 8

Covariance stationary time series

Answer 8

A time series is covariance stationary if its mean, variance, and covariances with lagged and leading values do not change over time. Covariance stationarity is a requirement for using AR models.

Question 9

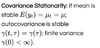
Autocovariance function

Answer 9

Autocovariance function refers to the tool used to quantify stability of the covariance structure. Its importance lies in its ability to summarize cyclical dynamics in a series that is covariance stationary.

Question 10

Autocorrelation function

Answer 10

Autocorrelation function refers to the degree of correlation and interdependency between data points in a time series. It recognizes the fact that correlations lend themselves to clearer interpretation than covariances.

Recall that the degree of correlation is measured on a continuum from — 1 to 1, whereas degrees of covariance employ a much wider range, which can be unwieldy in determining levels of association.

Question 11

The Durbin-Watson statistic - what it is and how to use

Answer 11

The Durbin-Watson statistic falls between zero and four.

• Two indicates no autocorrelation; aka, no serial correlation.
• Zero is perfect positive autocorrelation, and four is perfect negative autocorrelation.

Question 12

Partial autocorrelation function

Answer 12

Partial autocorrelation function refers to the partial correlation and interdependency between data in a time series that measures the association between data in a series after controlling for the effects of lagged observations

Question 13

Requirements for a series to be covariance stationary

Answer 13

A time series is covariance stationary if it satisfies the following three conditions:

1. Constant and finite expected value. The expected value of the time series is constant over time.
2. Constant and finite variance. The time series volatility around its mean (i.e., the distribution of the individual observations around the mean) does not change over time.
3. Constant and finite covariance between values at any given lag. The covariance of the time series with leading or lagged values of itself is constant.

Question 14

Explain the implications of working with models that are not covariance stationary

Answer 14

Requirements for covariance stationarity of a time series, though strict in appearance, make allowances for many series that are not covariance stationary. This is achieved by working with models that provide special treatment to trend and seasonality components that are stationary, which allows the remaining, or residual, cyclical component to be covariance stationary.

A nonstationary series can be transformed to appear covariance stationary by using transformed data, such as growth rates.

Question 15

White noise process

Answer 15

A time series process with a zero mean, constant variance, and no serial correlation is referred to as a white noise process (or zero-mean white noise). This is the simplest type of time series process and it is used as a fundamental building block for more complex time series processes. Even though a white noise process is serially uncorrelated, it may not be serially independent or normally distributed.

Variants of a white noise process include independent white noise and normal white noise. A time series process that exhibits both serial independence and a lack of serial correlation is referred to as independent white noise (or strong white noise) . A time series process that exhibits serial independence, is serially uncorrelated, and is normally distributed is referred to as normal white noise (or Gaussian white noise).

The dynamic structure of a white noise process includes the following characteristics:

• The unconditional mean and variance must be constant for any covariance stationary process.
• The lack of any correlation in white noise means that all autocovariances and autocorrelations are zero beyond displacement zero (displacement refers to the distance of a moving body from a central point). This same result holds for the partial autocorrelation function of white noise.
• Both conditional and unconditional means and variances are the same for an independent white noise process (i.e., they lack any forecastable dynamics).
• Events in a white noise process exhibit no correlation between the past and present.

Question 16

Why understanding white noise is tremendously important (two reasons)?

Answer 16

Understanding white noise is tremendously important for at least two reasons.

• First, processes with much richer dynamics are built up by taking simple transformations of white noise.
• Second, 1-step-ahead forecast errors from good models should be white noise. After all, if such forecast errors aren’t white noise, then they’re serially correlated, which means that they’re forecastable, and if forecast errors are forecastable then the forecast can’t be very good.

Question 17

Lag operator

Answer 17

Question 18

Wold’s representation theorem

Answer 18

Wold’s representation theorem is a model for the covariance stationary residual (i.e., a model that is constructed after making provisions for trends and seasonal components). Thus, the theorem enables the selection of the correct model to evaluate the evolution of covariance stationarity. Wold’s representation utilizes an infinite number of distributed lags, where the one-step-ahead forecasted error terms are known as innovations.

The general linear process is a component in the creation of forecasting models in a covariance stationary time series. It uses Wold’s representation to express innovations that capture an evolving information set. These evolving information sets move the conditional mean over time (recall that a requirement of stationarity is a constant unconditional mean). Thus, it can model the dynamics of a times series process that is outside of covariance stationarity (i.e., unstable).

As mentioned, applying Wold’s representation requires an infinite number of distributed lags. However, it is not practical to model an infinite number of parameters. Therefore, we need to restate this lag model as infinite polynomials in the lag operator because infinite polynomials do not necessarily contain an infinite number of parameters. Infinite polynomials that are a ratio of finite-order polynomials are known as rational polynomials. The distributed lags constructed from these rational polynomials are known as rational distributed lags. With these lags, we can approximate Wold’s representation. Autoregressive moving average (ARMA) process is a practical approximation for Wold’s representation.

Question 19

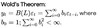
Calculate the sample mean and sample autocorrelation, and describe the Box-Pierce Q-statistic and the Ljung-Box Q-statistic

Answer 19

Question 20

Testing for white noise formulae

Answer 20

Question 21

What test can be used to check the hypothesis of no seasonality If the regression disturbances are white noise?

Answer 21

If the regression disturbances are white noise, the standard F-test can be used to test the hypothesis of no seasonality.

The hypothesis of no seasonality, in which case you could drop the seasonal dummies, corresponds to equal seasonal coefficients across seasons, which is a set of (s-1) linear restrictions. This is a standard F-test, but students need to be reminded that the tests’s legitimacy requires that the regression disturbances be white noise, which may well not hold in a regression on only trend and seasonals. Otherwise, the F statistic will not in general have the F distribution.

Question 22

The Ljung-Box Q-statistic vs. the Box-Pierce Q-statistic

Answer 22

The Ljung-Box Q-statistic is effectively similar to the Box-Pierce Q-statistic, except it is meant for small samples.

A slight modification of the Box-Pierce Q-statistic, designed to follow more closely the chi-squared distribution in small samples, is the Ljung-Box Q-statistic. Under the null hypothesis that y is white noise, the Ljung-Box Q-statistic is approximately distributed as a chisquared random variable. Note that the Ljung-Box Q-statistic is the same as the Box-Pierce Q statistic, except that the sum of squared autocorrelations is replaced by a weighted sum of squared autocorrelations, where the weights are (T+2)/(T-τ). For moderate and large T, the weights are approximately 1, so that the Ljung-Box statistic differs little from the Box-Pierce statistic.

Question 23

Describe the properties of the first-order moving average (MA(1)) process, and distinguish between autoregressive representation and moving average representation.

Answer 23

Question 24

Moving Average: 1st Order (MA(1)) - basic properties

Answer 24

Question 25

Describe the properties of a general finite-order process of order q (MA(q)) process.

Answer 25

Question 26

Moving Average: q Order (MA(q)) - basic properties

Answer 26

Question 27

Describe the properties of the first-order autoregressive (AR(1)) process, and define and explain the Yule-Walker equation.

Answer 27

When a moving average process is inverted it becomes an autoregressive representation, and is, therefore, more useful because it expresses the current observables in terms of past observables. An autoregressive process does not need to be inverted because it is already in the more favorable rearrangement, and is, therefore, capable of capturing a more robust relationship compared to the unadjusted moving average process. The first-order autoregressive [AR(1)] process must also have a mean of zero and a constant variance.

It is specified in the form of a variable regressed against itself in a lagged form. This relationship can be shown in the following formula:

y_t = φ*y_t-1 + ε_t

where:
y_t = the time series variable being estimated
y_t-1 = one-period lagged observation of the variable being estimated
ε_t = current random white noise shock
φ = coefficient for the lagged observation of the variable being estimated

In order for an AR(1) process to be covariance stationary, the absolute value of the coefficient on the lagged operator must be less than one (i.e., |φ| < 1).

In order to estimate the autoregressive parameters, such as the coefficient (φ), forecasters need to accurately estimate the autocovariance of the data series. The Yule-Walker equation is used for this purpose. When using the Yule-Walker concept to solve for the autocorrelations of an AR(1) process, we use the following relationship:

ρ_t = φ^t for t = 0,1,2,…

Moving average processes exhibit autocorrelation cutoff, which means the autocorrelations are essentially zero beyond the order of the process [an MA(1) process shows autocorrelation cutoff after time 1]. The significance of the Yule-Walker equation is that for autoregressive processes, the autocorrelation decays vary gradually. Consider an AR(1) process that is specified using the following formula:

y_t = 0.65y_t-1 + ε_t

The coefficient (φ) is equal to 0.65, and using the concept derived from the Yule-Walker equation, the first-period autocorrelation is 0.65 (i.e., 0.65¹), the second-period autocorrelation is 0.4225 (i.e., 0.65²), and so on for the remaining autocorrelations.

Question 28

AutoRegressive: 1st Order (AR(1)) - basic properties

Answer 28

Question 29

Describe the properties of a general p^th order autoregressive (AR(p)) process.

Answer 29

Question 30

AutoRegressive: p Order (AR(p)) - basic properties

Answer 30

Question 31

Define and describe the properties of the autoregressive moving average (ARMA) process

Answer 31

Stock prices might show evidence of being influenced by both unobserved shocks (the moving average component) and their own lagged behavior (the autoregressive component). This more complex relationship is called an autoregressive moving average (ARMA) process and is expressed by the following formula:

y_{t =} φy_t-1 + ε_t + θε_t-1

where:
y_t = the time series variable being estimated
φ = coefficient for the lagged observations of the variable being estimated
y_t-1 = one-period lagged observation of the variable being estimated
ε_t = current random white noise shock
θ = coefficient for the lagged random shocks
ε_t-1 = one-period lagged random white noise shock

You can see tha the ARMA formula merges the concepts of an AR process and an MA process. Just as with the AR process, the autocorrelations in an ARMA process will also decay gradually for essentially the same reasons.

Just as moving average models can be extrapolated to the q^th observation and autoregressive models can be taken out to the p^th observation, ARMA models can be used in the format of an ARMA(p,q) model. For example, an ARMA(3,1) model means 3 lagged operators in the AR portion of the formula and 1 lagged operator on the MA portion. This flexibility provides the highest possible set of combinations for time series forecasting of the three models discussed in this topic.

Question 32

AutoRegressive Moving Average: (ARMA(p,q)) - basic properties

Answer 32

Question 33

Motivations for using ARMA model

Answer 33

Autoregressive and moving average models are often combined in attempts to obtain better and more parsimonious approximations to the Wold representation, yielding the autoregressive moving average process, ARMA(p,q) for short.

As with moving average and autoregressive processes, ARMA processes also have direct motivation.

• First, if the random shock that drives an autoregressive process is itself a moving average process, then it can be shown that we obtain an ARMA process.
• Second, ARMA processes can arise from aggregation. For example, sums of AR processes, or sums of AR and MA processes, can be shown to be ARMA processes.
• Finally, AR processes observed subject to measurement error also turn out to be ARMA processes.

Question 34

Describe the application of AR and ARMA processes

Answer 34

A forecaster might begin by plotting the autocorrelations for a data series and find that the autocorrelations decay gradually rather than cut off abruptly. In this case, the forecaster should rule out using a moving average process. If the autocorrelations instead decay gradually, he should consider specifying either an autoregressive (AR) process or an autoregressive moving average (ARMA) process. The forecaster should especially consider these alternatives if he notices periodic spikes in the autocorrelations as they are gradually decaying. For example, if every 12^th autocorrelation jumps upward, this observation indicates a possible seasonality effect in the data and would heavily point toward using either an AR or ARMA model.

Question 35

Define and distinguish between volatility, variance rate, and implied volatility, square root of time rule

Answer 35

The volatility of a variable, σ, is represented as the standard deviation of that variable’s continuously compounded return. With option pricing, volatility is typically expressed as the standard deviation of return over a one-year period. This differs from risk management, where volatility is typically expressed as the standard deviation of return over a one-day period.

The traditional measure of volatility first requires a measure of change in asset value from period to period. The calculation of a continuously compounded return over successive days is as follows:

u_i = ln (S_i/S_i-1)

where:
S_i = asset price at time i

This is similar to the proportional change in an asset, which is calculated as follows:

u_i = (S_i - S_i-1)/S_i-1

From a risk management perspective, the daily volatility of an asset usually refers to the standard deviation of the daily proportional change in asset value.

By assuming daily returns are independent with the same level of variation, daily volatility can be extended over a number of days, T, by multiplying the standard deviation of the return by the square root of T. This is known as the square root of time rule. Note that when converting daily volatility to annual volatility, the usual practice is to use the square root of 252 days, which is the number of business days in a year, as opposed to the number of calendar days in a year.

Risk managers may also compute a variable’s variance rate, which is simply the square of volatility (i.e., standard deviation squared: σ²). In contrast to volatility, which increases with the square root of time, the variance of an asset’s return will increase in a linear fashion over time.

In addition to variance and standard deviation, which are computed using historical data, risk managers may also derive implied volatilities. The implied volatility of an option is computed from an option pricing model, such as the Black-Scholes-Merton (BSM) model. The volatility of an asset is not directly observed in the BSM model, so we compute implied volatility as the volatility level that will result when equating an option’s market price to its model price.

Question 36

Describe the power law

Answer 36

In practice the distribution of asset price changes is more likely to exhibit fatter tails than the normal distribution. Thus, heavy-tailed distributions can be used to better capture the possibility of extreme price movements (e.g., a five-standard-deviation move). An alternative approach to assuming a normal distribution is to apply the power law.

The power law states that when X is large, the value of a variable V has the following property:

P(V > X) = K*X^-α

where:
V = the variable
X = large value of V
K and α = constants

By taking the logarithm of both sides in the power law equation, we can perform regression analysis to determine the power law constants, K and α:

In [P(V > X)] = In (K) — αIn (X)

In this case, the dependent variable, ln[P(V > X)], can be plotted against the independent variable, ln(X). Furthermore, if we assume that X represents the number of standard deviations that a given variable will change, we can determine the probability that V will exceed a certain number of standard deviations. For example, if regression analysis indicates that K = 8 and α = 5, the probability that the variable will exceed four standard deviations will be equal to 8*4^-5 = 0.0078 or 0.78%. The power law suggests that extreme movements have a very low probability of occurring, but this probability is still higher than what is indicated by the normal distribution.

Question 37

Autoregressive conditional heteroskedasticity model, ARCH(m)

Answer 37

The most frequently used model is an autoregressive conditional heteroskedasticity model, ARCH(m), which can be represented by:

Question 38

EWMA - the idea

Answer 38

Question 39

Exponentially weighted moving average (EWMA) model

Answer 39

The exponentially weighted moving average (EWMA) model is a specific case of the general weighting model. The main difference is that the weights are assumed to decline exponentially back through time. This assumption results in a specific relationship for variance in the model:

σ_n² = λσ_n-1² + (1 - λ)u_n-1²

where:
λ = weight on previous volatility estimate (λ between zero and one)

The simplest interpretation of the EWMA model is that the day-n volatility estimate is calculated as a function of the volatility calculated as of day n — 1 and the most recent squared return. Depending on the weighting term X, which ranges between zero and one, the previous volatility and most recent squared returns will have differential impacts. High values of λ will minimize the effect of daily percentage returns, whereas low values of λ will tend to increase the effect of daily percentage returns on the current volatility estimate.

One benefit of the EWMA is that it requires few data points. Specifically, all we need to calculate the variance is the current estimate of the variance and the most recent squared return.

Question 40

GARCH(1,1) model

Answer 40

Question 41

Explain mean reversion and how it is captured in the GARCH(1,1) model

Answer 41

Question 42

Estimation and Performance of GARCH Models

Answer 42

One way to estimate volatility (e.g., variance) is to use a maximum likelihood estimator. Maximum likelihood estimators select values of model parameters that maximize the likelihood that the observed data will occur in a sample.

GARCH models are estimated using maximum likelihood techniques. The estimation process begins with a guess of the model’s parameters. Then a calculation of the likelihood function based on those parameter estimates is made. The parameters are then slightly adjusted until the likelihood function fails to increase, at which time the estimation process assumes it has maximized the function and stops. The values of the parameters at the point of maximum value in the likelihood function are then used to estimate GARCH model volatility.

Question 43

Explain how GARCH models perform in volatility forecasting

Answer 43

If GARCH models do a good job at explaining past volatility, how well do they forecast future volatility?

The simple answer to this question is that GARCH models do a fine job at forecasting volatility from a volatility term structure perspective (e.g., estimates of volatility given time to expiration for options). Even though the actual volatility term structure figures are somewhat different from those forecasted by GARCH models, GARCH-generated volatility data does an excellent job in predicting how the volatility term structure responds to changes in volatility.

This modeling tool is quite frequently used by financial institutions when estimating exposure to various option positions.

Question 44

Define correlation and covariance and differentiate between correlation and dependence

Answer 44

Correlation is mathematically determined by dividing the covariance between two random variables, cov(X,Y), by the product of their standard deviations, σ_Xσ_Y.

ρ_X,Y = cov(X, Y)/σ_Xσ_Y

Multiplying each side of this equation by σ_Xσ_Y provides the formula for calculating covariance:

cov(X,Y) = ρ_{X,Y *} σ_Xσ_Y

In practice, it is necessary to first calculate the covariance between two random variables using the following equation and then solve for the standardized correlation.

cov(X, Y) = E[(X — E(X)) x (Y - E(Y))] = E(X, Y) - E(X) x E( Y)

In this covariance equation, E(X) and E(Y) are the means or expected values of random variables X and Y, respectively. E(X,Y) is the expected value of the product of random variables X and Y.

Variables are defined as independent variables if the knowledge of one variable does not impact the probability distribution for another variable. In other words, the conditional probability of V₂ given information regarding the probability distribution of V1 is equal to the unconditional probability of V₂ as expressed in the following equation:

P(V₂ |V₁=x) = P(V₂)

A correlation of zero between two variables does not imply that there is no dependence between the two variables. It simply implies that there is no linear relationship between the two variables, but the value of one variable can still have a nonlinear relationship with the other variable.

The coefficient of correlation is a statistical measure of linear dependency.

Question 45

Calculate covariance using the EWMA model

Answer 45

Question 46

Calculate covariance using the GARCH(1,1) model

Answer 46

Question 47

Apply the consistency condition to covariance

Answer 47

Question 48

Positive Semi-definiteness

Answer 48

Question 49

Describe the procedure of generating samples from a bivariate normal distribution.

Answer 49

Question 50

Bi-variate normal distributions

Answer 50

Question 51

Describe properties of correlations between normally distributed variables when using a one-factor model.

Answer 51

Question 52

Correlated normals

Answer 52

Question 53

One Factor model

Answer 53

Question 54

Define copula and describe the key properties of copulas and copula correlation

Answer 54

Suppose we have two marginal distributions of expected values for variables X and Y.

The marginal distribution of variable X is its distribution with no knowledge of variable Y. The marginal distribution of variable Y is its distribution with no knowledge of variable X.

If both distributions are normal, then we can assume the joint distribution of the variables is bivariate normal. However, if the marginal distributions are not normal, then a copula is necessary to define the correlation between these two variables.

A copula creates a joint probability distribution between two or more variables while maintaining their individual marginal distributions. This is accomplished by mapping the marginal distributions to a new known distribution.

Suppose we have two triangular marginal distributions for two variables X and Y as illustrated in the Figure.

The key property of a copula correlation model is the preservation of the original marginal distributions while defining a correlation between them. A correlation copula is created by converting two distributions that may be unusual or have unique shapes and mapping them to known distributions with well-defined properties, such as the normal distribution. As mentioned, this is done by mapping on a percentile-to-percentile basis.

Therefore, using a copula is a way to indirectly define a correlation structure between two variables when it is not possible to directly define correlation.

Question 55

Sklar Theorem

Answer 55

Question 56

Describe the Gaussian copula, Student’s t-copula, multivariate copula, and one factor copula

Answer 56

A Gaussian copula maps the marginal distribution of each variable to the standard normal distribution. The mapping of each variable to the new distribution is done based on percentiles.

Other types of copulas are created by mapping to other well-known distributions. The Student’s t-copula is similar to the Gaussian copula. However, variables are mapped to distributions of U₁ and U₂ that have a bivariate Student’s t-distribution rather than a normal distribution.

The following procedure is used to create a Student’s t-copula assuming a bivariate Student’s t-distribution with f degrees of freedom and correlation ρ.

• Step 1: Obtain values of χ by sampling from the inverse chi-squared distribution with f degrees of freedom.
• Step 2: Obtain values by sampling from a bivariate normal distribution with correlation ρ.
• Step 3: Multiply (f/χ)^0.5 by the normally distributed samples.

A multivariate copula is used to define a correlation structure for more than two variables. Suppose the marginal distributions are known for N variables: V₁, V₂, …, V_N. Distribution V_i for each i variable is mapped to a standard normal distribution, U_i. Thus, the correlation structure for all variables is now based on a multivariate normal distribution.

Factor copula models are often used to define the correlation structure in multivariate copula models. The nature of the dependence between the variables is impacted by the choice of the U_i distribution. The following equation defines a one-factor copula model where F and Z_i are standard normal distributions:

U_i = α_iF + (1-α_i²)^0.5Z_i

The U_i distribution has a multivariate Student’s t-distribution if Z_i and F are assumed to have a normal distribution and a Student’s t-distribution, respectively. The choice of U_i determines the dependency of the U variables, which also defines the covariance copula for the V variables.

A practical example of how a one-factor copula model is used is in calculating the value at risk (VaR) for loan portfolios. A risk manager assumes a one-factor copula model maps the default probability distributions for different loans. The percentiles of the one-factor distribution are then used to determine the number of defaults for a large portfolio.

Question 57

Joint CDF using copulas

Answer 57

Question 58

Explain tail dependence

Answer 58

There is greater tail dependence in a bivariate Student’s t-distribution than a bivariate normal distribution. In other words, it is more common for two variables to have the same tail values at the same time using the bivariate Student’s t-distribution. During a financial crisis or some other extreme market condition, it is common for assets to be highly correlated and exhibit large losses at the same time. This suggests that the Student’s t-copula is better than a Gaussian copula in describing the correlation structure of assets that historically have extreme outliers in the distribution tails at the same time.

Question 59

Steps required to conduct a Monte Carlo simulation

Answer 59

There are four basic steps required to conduct a Monte Carlo simulation.

• Step 1: Specify the data generating process (DGP)
• Step 2: Estimate an unknown variable or parameter
• Step 3: Save the estimate from step 2
• Step 4: Go back to step 1 and repeat this process N times

Question 60

Describe ways to reduce Monte Carlo sampling error

Answer 60

Question 61

Explain how to use antithetic variate technique to reduce Monte Carlo sampling error.

Answer 61

The use of antithetic variates results in a negative covariance between the original random draws and their complements (i.e., antithetic variates). Thus, the use of antithetic variates causes the error terms to be independent for the two sets, which results in a negative covariance term in the variance equation. This negative relationship means that the Monte Carlo sampling error must always be smaller using this approach.

Question 62

Explain how to use control variates to reduce Monte Carlo sampling error and when it is effective

Answer 62

The control variate technique is a widely used method to reduce the sampling error in Monte Carlo simulations. A control variate involves replacing a variable x (under simulation) that has unknown properties with a similar variable y that has known properties.

Question 63

Describe the benefits of reusing sets of random number draws across Monte Carlo experiments and how to reuse them

Answer 63

Reusing sets of random number draws across Monte Carlo experiments reduces the estimate variability across experiments by using the same set of random numbers for each simulation. Normally, a user would not desire to reuse the same random draws. However, in certain situations this technique is useful. Two examples of reusing sets of random numbers are for testing the power of the Dickey-Fuller test (used to determine whether a time series is covariance stationary) or for different experiments with options using time series data.

• Dickey-Fuller (DF) test*. Suppose an analyst wants to examine the DF test for sample sizes of 1,000 to test whether or not a particular market follows a random walk or contains a drift element. The analyst could reuse the same set of standard normal random variables for each simulation run while testing with different DF parameters. Using the same set of random numbers for each Monte Carlo experiment reduces the sampling variation across experiments. In this case, the sampling variability is reduced, but the accuracy of the actual estimates is not increased.
• Different experiments*. Another example where reusing sample data is useful is in testing differences among options. For example, suppose an analyst is examining option prices that are similar in all aspects except for time to maturity. The analyst could simulate a long time series of random draws and then split this longer time series into shorter time frames. A six-month time series of data could be subdivided into three sets of two-month maturity options or six sets of one-month maturity options. Using the same random number data set reduces the variability of simulated option prices across maturities.

Question 64

Describe the bootstrapping method and its advantage over Monte Carlo simulation

Answer 64

Another way to generate random numbers is the bootstrapping method. The bootstrapping approach draws random return data from a sample of historical data. Under traditional Monte Carlo simulation, data sets are created by selecting random variables drawn from a pre-determined probability distribution. The bootstrapping method uses actual historical data instead of random data from a probability distribution. In addition, bootstrapping repeatedly draws data from a historical data set and replaces the data so it can be drawn again.

An obvious advantage of the bootstrapping approach is that no assumptions are made regarding the true distribution of the parameter estimate that is being examined. This implies that it can include extreme events that have occurred in the past (e.g., during a financial crisis). Inclusion of outliers will produce a distribution that has fatter tails than the normal distribution, which allows for a more realistic view of actual return data. Thus, the bootstrapping methodology generates a collection of data sets with approximately the same distribution properties as the original data. However, any dependency of variables or autocorrelations in the original data set will no longer be present, because variables are not drawn in the same sequence as the original data set.

Question 65

Describe situations where the bootstrapping method is ineffective

Answer 65

Two situations that cause the bootstrapping method to be ineffective are outliers in the data and non-independent data.

• If outliers exist in the data, the inferences drawn from parameter estimates may not be accurate depending on how many times the outliers are included in the bootstrapped sample. Because replacement is used in the bootstrap method, outliers could be drawn more often, causing the bootstrap distribution to have fatter tails. Alternatively, not drawing the outlier in the bootstrapped sample may lead to the opposite conclusions regarding the parameter estimate statistical properties. Recall that a major advantage of the bootstrapping approach over traditional approaches is that it does not require any assumptions of the probability distribution of the sampled data. Thus, the best way to mitigate this issue is to have a large number of replications.
• If autocorrelation exists in the original sample data, then the original historical data are not independent of one another. A technique known as a moving block bootstrap is used to overcome the problem of autocorrelation. Blocks of data are examined at one time in order to preserve the original data dependency.

Question 66

Describe the pseudo-random number generation method and how a good simulation design alleviates the effects the choice of the seed has on the properties of the generated series

Answer 66

Question 67

Describe disadvantages of the simulation approach to financial problem solving

Answer 67