Swaps, Credit default swaps and Interest Rate Derivatives

Question 1

Plain Vanilla Swap

Answer 1

Fixed for floating in the same currency

Question 2

• L_i (m)
• B₀ (h_j)

Answer 2

• M-day Libor on day i
• Present value factor on a zero-coupon instrument paying $1 on day j

Question 3

Value of 1.0 in principal at h_{n - 1}

Answer 3

Question 4

FS(0, n, m)

Answer 4

Fixed swap interest payment rate

Question 5

Present value of a series of fixed interest payments at the swap rate FS(0, n, m)

Answer 5

Question 6

FS(0, n, m) price

Answer 6

*

Question 7

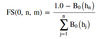
Swap value on day t

Answer 7

• Fixed payments = FS(0, n, m) * Σ B_t (h_j) + 1 * B_t (h_n)
• Floating payments = [(Value of the first floating payment on day 0) + 1] * B_t (h₁)
• Value of the first floating payment on day 0 = L₀ (m) * (m/360)
• Value = floating payments - fixed payments

Question 8

Swap value (pay fixed/receive equity return)

Answer 8

Question 9

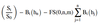
Swap value (pay floating/receive equity return)

Answer 9

(S_t / S₀) - Value of the first floating payment on day 0 * B_t (h1)

Question 10

CMT

Answer 10

Constant Maturity Treasury

Question 11

OIS

Answer 11

Overnight Index Swap

Question 12

Amortizing and accreting swaps are swaps in which the notional principal changes according to a formula related to the underlying

Answer 12

The more common of the two is the amortizing swap, sometimes called an index amortizing swap. In this type of interest rate swap, the notional principal is indexed to the level of interest rates

Question 13

• Diff swap
• Arrears swap
• Capped swap
• Floored swap

Answer 13

• Combines elements of interest rate, currency, and equity swaps
• The floating payment is set at the end of the period and the interest is paid at that same time
• The floating payments have a limit as to how high they can be
• The floating payments have a limit as to how low they can be

Question 14

Swaption

Answer 14

An option to enter into a swap

Question 15

• Payer swaption
• Receiver swaption

Answer 15

• Allows the holder to enter into a swap as the fixed-rate payer and floating-rate receiver
• Allows the holder to enter into a swap as the fixed-rate receiver and floating-rate payer

Question 16

Payoff of a payer swaption

Answer 16

Question 17

Payoff of a receiver swaption

Answer 17

Question 18

Variation margin

Answer 18

Additional margin deposited on a futures to get back to the initial margin

Question 19

Invoice price

Answer 19

Contract size x Futures settlement price x Conversion factor + accrued interest

Question 20

Cheapest-to-deliver

Answer 20

The bond with the highest implied repo rate

Question 21

Converted price

Answer 21

Futures price x Conversion factor

Question 22

Delivery options of the short on a CBOT Treasury bond futures contract

Answer 22

• Quality or swap option
• Timing option
• Wild card option

Question 23

Credit derivatives types

Answer 23

• Total return swap
• Credit spread option
• Credit-linked note
• Credit default swap (CDS)

Question 24

CDS terminology

Answer 24

• Single-name CDS - on one specific borrower
• Reference entity - the borrower
• Reference obligation - the particular debt instrument
• Cheapest-to-deliver obligation - the payoff on which the CDS is based

Question 25

ISDA

Answer 25

International Swaps and Derivatives Association

Question 26

CDS industry

• Seller is
• Buyer is

Answer 26

• Long
• Short

Question 27

Credit and succession events

Answer 27

• Bankruptcy
• Failure to pay
• Restructuring
• Succession event

Question 28

• Payout ratio
• Payout amount

Answer 28

• 1 - recovery rate (%)
• Payout ratio x Notional

Question 29

Hazard rate

Answer 29

The probability that an event will occur given that it has not already occurred

Question 30

• Protection leg
• Premium leg

Answer 30

• The contingent payment that the credit protection seller may have to make to the credit protection buyer
• The series of payments the credit protection buyer promises to make to the credit protection seller

Question 31

Present value of credit spread

Answer 31

Upfront premium + Present value of the fixed coupons

Question 32

Approximation of the present value of a stream of payments on CDS

Answer 32

Question 33

The convention in the CDS market starting in recent years is for standardized coupons

Answer 33

• 1% for investment-grade debt
• 5% for high-yield debt

Question 34

Change in value of the CDS for a given change in spread

Answer 34

• Profit for the buyer of protection ≈ +Change in spread (bps) × Duration × Notional
• % Change in CDS price = Change in spread (bps) × Duration

Question 35

Monetizing

Answer 35

The conversion of the value of a financial transaction into currency

Question 36

Naked credit default swap

Answer 36

A credit protection purchased by a party with no exposure to the reference entity

Question 37

Curve trade

Answer 37

Involves buying a CDS of one maturity and selling a CDS on the same reference entity with a different maturity

Question 38

Basis trade

Answer 38

A trade based on the pricing of credit in the bond market versus the price of the same credit in the CDS market

Question 39

Synthetic CDO

Answer 39

Created by combining a portfolio of default-free securities with a combination of credit default swaps undertaken as protection seller