Brainscape's Knowledge GenomeTM

Browse over 1 million classes created by top students, professors, publishers, and experts.


See full index

CFA Level 2 COPY (930) > Options > Flashcards

Options Flashcards

1
Q

Moneyness of an option

A

Refers to the relationship between the price of the underlying and the exercice price

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
2
Q

Option premium

A

Sometimes used instead of option price

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
3
Q

Long-term equity anticipatory securities (LEAPS)

A

Options with expiration of several years

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
4
Q

Options Clearing Corporation (OCC)

A

A clearinghouse that manages options

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
5
Q

Interest rate option settlement

A

The settlement is done at the end of the period covered by the option and not at expiration

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
6
Q

Interest rate cap

A
  • An interest rate cap is a series of European interest call options (called caplets), with a particular interest rate, each of which expires on the date the floating loan rate will be reset
  • In an interest rate cap, the seller agrees to compensate the buyer for the amount by which an underlying short-term rate exceeds a specified rate on a series of dates during the life of the contract
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
7
Q

Interest rate floor

A
  • An interest rate floor is a series of European interest floor options (called floorlets), with a particular interest rate, each of which expires on the date the floating loan rate will be reset
  • In an interest rate floor, the seller agrees to compensate the buyer for a rate falling below the specified rate during the contract period
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
8
Q

Interest rate collar

A

A collar is a combination of a long (short) cap and short (long) floor, struck at different rates

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
9
Q

Zero-cost collar

A

When the price received for going short either the floor or the cap is precisely the price required to go long the other one

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
10
Q

Options notation - European vs American

A
  • c0, cT = price of European call today and at expiration
  • C0, CT = price of American call today and at expiration
  • p0, pT = price of European put today and at expiration
  • P0, PT = price of American put today and at expiration
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
11
Q

Options value vocabulary

A
  • Intrinsic value = exercise value
  • Time value = speculative value
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
12
Q

Options minimum and maximum value

A
  • c0 ≥ Max [0, S0 − X / (1+r)T]
  • C0 ≥ Max [0, S0 − X / (1+r)T]
  • p0 ≥ Max [0, X / (1+r)T − S0]
  • P0 ≥ Max (0, X − S0)
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
13
Q

A lower bound combination for European Calls

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
14
Q

A lower bound combination for European Puts

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
15
Q

Fiduciary call and protective put values

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
16
Q

Put-call parity equation

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
17
Q

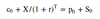
Fiduciary Call

A

A combination of a European call and a risk-free bond that matures on the option expiration day and has a face value equal to the exercise price of the call

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
18
Q

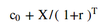
Protective Put

A

An option strategy in which a long position in an asset is combined with a long position in a put

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
19
Q

Synthetic put

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
20
Q

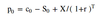
Synthetic call

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
21
Q

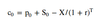
Synthetic call values

A
22
Q

Synthetic put values

A
23
Q

Lower bounds for European options considering cash flows

A
24
Q

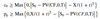
Put-call parity considering cash flows

A
25
Q

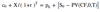
The hedge ratio

A
26
Q

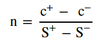
Value of c and pi in a hedged portfolio

A
27
Q

Value of c+ and c- in a two-period binomial hedged portfolio

A
28
Q

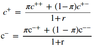
The hedge ratio in a two-period binomial portfolio

A
29
Q

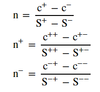
Black-Scholes-Merton formula

A
30
Q

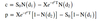
Black-Scholes-Merton d1 & d2 formula

A
31
Q

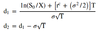
American versus European option values considering cash flows

A

When the underlying makes no cash payments, C0 = c0

When the underlying makes cash payments during the life of the option, early exercise can be worthwhile and C0 can thus be higher than c0

The American put is nearly always worth more than the European put: P0 > p0

32
Q

Lower bounds for European options of futures

A
33
Q

Lower bounds for American options of futures

A
34
Q

Put-call-forward parity

A
35
Q

Put-call-forward parity formula

A
36
Q

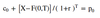
Synthetic forward contract

A
37
Q

Black-Scholes-Merton for futures formula

A
38
Q

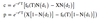
Black-Scholes-Merton for futures d1 & d2 formula

A
39
Q

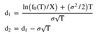
Price of call and put options relative to interest rate

A
  • When rates are higher:
    • Call prices are higher
    • Put prices are lower
  • When rates are lower:
    • Call prices are lower
    • Put prices are higher
40
Q

Effect of volatility on put and call option prices

A
  • Increases the prices of both of them
    • The upside effect increases the call price and does not hurt the put
    • The downside effect increases the put price and does not hurt the call
41
Q

The different measures of option price sensitivity

A
  • Delta is the sensitivity of the option price to a change in the price of the underlying
  • Gamma is a measure of how well the delta sensitivity measure will approximate the option price’s response to a change in the price of the underlying
  • Rho is the sensitivity of the option price to the risk-free rate
  • Theta is the rate at which the time value decays as the option approaches expiration
  • Vega is the sensitivity of the option price to volatility
42
Q

European put option prices can be either higher or lower the longer the time to expiration

A

American put option prices are always higher the longer the time ot expiration

43
Q

Option delta

A
  • Change in the option price / Change in the underlying price
  • Approximately N(d1) for calls and N(d1) - 1 for puts
44
Q

Hedging with delta (dynamic hedging)

A
  • To hedge options → buy delta * (number of options)
  • To hedge an underlying position → buy [1 / delta] * (number of unit of the underlying)
45
Q

Option delta as the price moves

A
  • The delta of a call will move towards 1.0 as the underlying moves up and towards 0 as it moves down
  • The delta of a put will move towards -1.0 as the underlying moves down and towards 0 as it moves up
46
Q

Option delta when the underlying price does not move and the option gets closer to maturity

A
  • The delta of a call will move towards 1.0 if the call is in-the-money or 0 if it is not
  • The delta of a put will move towards - 1.0 if the call is in-the-money or 0 if it is not
47
Q

We can treat European options on futures the same way as options on forwards

A

American options on futures will differ from American options on forwards

48
Q

Black-Scholes-Merton assumptions

A
  • The Underlying Price Follows a Geometric Lognormal Diffusion Process
  • The Risk-Free Rate Is Known and Constant
  • The Volatility of the Underlying Asset Is Known and Constant
  • There Are No Taxes or Transaction Costs
  • There Are No Cash Flows on the Underlying
  • The Options Are European
49
Q

Black-Scholes-Merton notation

A
  • S0 is the price of the underlying
  • X is the exercise price
  • rc is the continuously compounded risk-free rate
  • T is the time to expiration
  • σ is the annualized standard deviation of the continuously compounded return on the stock
  • N(d1) and N(d2) represent normal probabilities based on the values of d1 and d2
50
Q

A hedged portfolio should grow in value at the risk-free rate (H+ & H-)

A
  • H+ = H (1+ r), or
  • H– = H (1 + r)
51
Q

Gamma characteristics

A
  • Gamma is larger when there is more uncertainty about whether the option will expire in- or out-of-the-money
  • Gamma will tend to be large when the option is at-the-money and close to expiration
  • Delta will be a poor approximation for the option’s price sensitivity when it is at-the-money and close to the expiration day
52
Q

Interest rate put or call option in relation to floors and caps

A
  • A 2-year floor equals the value of a comparable 1-year European put option (1-year floorlet) plus the value of a comparable 2-year European put option (2-year floorlet)
  • The value of the 1-year put option is equal to the value of a comparable 1-year European put option (1-year floorlet)
  • Vice-versa for calls and caps

CFA Level 2 COPY (930) (13 decks)

Brainscape helps you reach your goals faster, through stronger study habits.
© 2024 Bold Learning Solutions. Terms and Conditions