Some Distribution Theory

Question 1

What distribution does Y have ?

Answer 1

Question 2

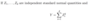
If Z is a standard normal random quantity, then what does E[Z²] and Var[Z²] equal?

Answer 2

• E[Z²] = 1
• Var[Z²] = 2

Question 3

If Z is a standard normal random quantity and Y is the sum between 1 and d of the Z_i² values and Y ∼ 𝒳_d² then what does E[Y] and Var[Y] equal?

Answer 3

• E[Y] = d
• Var[Y] = 2d

Question 4

If Z is a standard normal random quantity and Y is the sum between 1 and d of the Z_i² values and Y ∼ 𝒳_d² then why does E[Y] = d?

Answer 4

Question 5

If Z is a standard normal random quantity and Y is the sum between 1 and d of the Z_i² values and Y ∼ 𝒳_d² then why does Var[Y] = 2d?

Answer 5

Question 6

If Z is a standard normal random quantity and Y is the sum between 1 and d of the Z_i² values, for large d large how is Y approximately distributed?

Answer 6

Y ∼ N(d, 2d)

By the central limit theorem

Question 7

If U ∼ 𝒳_f² and V ∼ 𝒳_g², U and V independent, what does W = U + V have?

Answer 7

W ∼ 𝒳_f+g²

Question 8

If Y ∼ 𝒳_d² what is the pdf of Y?

Answer 8

Question 9

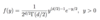
What is Γ(t) called?

Answer 9

The gamma funciton

Question 10

What is the equation for Γ(t)?

Answer 10

Question 11

What are three very useful properties of the gamma function?

Answer 11

Question 12

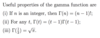
The chi-squqared distribution is a special case of the gamma distribution with what two parameters?

Answer 12

1. Shape parameter α > 0
2. Scale parameter λ > 0

Question 13

If Y ∼ Γ(α, λ) what is the pdf of Y?

Answer 13

Question 14

What is Y ∼ 𝒳_d² equivalent to in the gamma distribution?

Answer 14

Y ∼ Γ(½d, d)

Question 15

What is Y ∼ exp(λ) equivalent to in the gamma distribution?

Answer 15

λ ∼ Γ(1, λ)

Question 16

What is the pdf of the exponential distribution?

Answer 16

Question 17

If Y ∼ Γ(α, λ) what does E[Y] and Var[Y] equal?

Answer 17

Question 18

If Y ∼ Γ(α, λ) prove that E[Y] = α / λ and say how you can use this to prove Var[Y] = α / λ².

Answer 18

Var[Y] = E[Y²] - (E[Y])²

So use the expected value from before and inegrate y²f(y) to find the first part.

Question 19

What is the distribution of W

Answer 19

Question 20

Prove

Answer 20

See sheet 4 (Need to add)