Large Sample Properties of Maximum Likelihood Estimators

Question 1

If X ∼ Bi(n,p), and X = k what is the maximum liklihood estimator p^{^} equal to?

Answer 1

p^{^} = k/n

Question 2

If X = (X₁, … , X_n) is an iid sample, size n, from Po(λ) what is the sufficent statistic for λ and the MLE?

Answer 2

• ẍ is a sufficient statistic for λ
• λ^{^} = ẍ
• Note: two dots = bar

Question 3

If X = (X1, … , Xn) is an iid sample, size n, from N(𝛍, σ²) what is the sufficent statistic for (𝛍, σ²) and their MLE?

Answer 3

• (ẍ, ss) are the sufficient statistics for (𝛍, σ²)
• 𝛍^{^} = ẍ
• σ^{2^} = ss/n
• Note: two dots = bar
• ss =

Question 4

Answer 4

Question 5

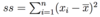
What is 𝐼(θ) called?

Answer 5

The Fisher’s information for θ in sample of size 1

Question 6

What is n𝐼(θ) called?

Answer 6

The Fisher’s information for θ in sample of size n

Question 7

What is the equation for 𝐼(θ) ?

Answer 7

Question 8

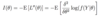
For n large what is the approximate (1- α) level confidence interval for θ?

Answer 8

Question 9

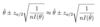
What is an alternate estimate for n𝐼(θ)?

Answer 9

-L’‘(θ^{^})

Question 10

What is the observed information in sample?

Answer 10

-L’‘(θ^{^})

Question 11

Using the observed information in the sample when s an approximate distribution for θ^{^}?

Answer 11

N(θ, 1/(-L’‘(θ^{^}))

Question 12

Using the observed information in the sample what is an alternative approximate confidence interval for θ^{^}?

Answer 12

Question 13

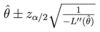
What is the Cramer Rao inequality and why is it used?

Answer 13

Question 14

What are unbiased estimators?

Answer 14

Estimators which achieve the lower bound of the Cramer Rao inequality

Question 15

How efficent are maximum likelihood estimators?

Answer 15

Asympototically efficient