Goodness of Fit Tests

Question 1

If Y ∼ Bi(n, p), what is the equation for P[Y = k]?

Answer 1

Question 2

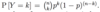
What are the three conditions for the binomial distribution?

Answer 2

• n independent trials
• two outcomes, success or failure
• probability of success, p, is constant

Question 3

If Y ∼ Bi(n, p) what is 𝔼[Y] and Var[Y]?

Answer 3

• 𝔼[Y] = np
• Var[Y] = np(1 - p)

Question 4

If Y ∼ Bi(n, p), for large n what is the distrubtion of Y approximately equal to?

Answer 4

N(np, np(1 - p))

Question 5

What do k, p_i, Oi, and E_i, stand for in the Chi-square test?

Answer 5

• k - the number of outcomes or cells
• p_i - the probability of outcome i
• O_i - the number of times outcome i is oberved
• E_i - the expected value of O_i, E_i = np_i

Question 6

What does Var[O_i] and E[O_i] equal?

Answer 6

• Var[O_i] = np_i (1 - p_i)
• E[O_i] = np_i

Question 7

What is the test statistic for the Chi-square goodness of fit test?

Answer 7

Question 8

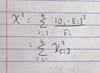
What is the distrubtion of O_i?

Answer 8

O_i ∼ Bi(n, p_i)

Question 9

What does E[𝒳²] equal ? And Why?

Answer 9

Question 10

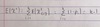
Finish this theorm:

Given H₀ the sampling distribution of 𝒳², with k cells, for large n, is approximately …

Answer 10

Given H₀ the sampling distribution of 𝒳², with k cells, for large n, is approximately a chi-squared distribution with k - 1 degrees of freedom.

Question 11

What does each E_i have to be bigger than to justify a chi-squared approximation?

Answer 11

E_i ≧ 5

Question 12

What do you do if E_i​ < 5 for some cells?

Answer 12

Pool the cells and add up the O_i’s

Question 13

What are the degrees of freedom for a chi-squared distribution when we estimated s independent parameters?

Answer 13

k - s - 1

Question 14

Do small or large values for 𝒳² cast doubt on H₀?

Answer 14

Large

Question 15

How can you perform a significance test of H₀ at level α, using the Chi-squared goodness of fit test?

Answer 15

• Calculate 𝒳²
• Identify the value V_α such that P[𝒳² > V_α] = α
• The test rejects H₀ at significance level α (or significant at level α) if 𝒳² > V_α
• If 𝒳² < V_α say test does not reject at level α (or result not significant at level α)

Question 16

What is a p-value?

Answer 16

The probability that test statistic is larger than the observed value, if H₀ is true

Question 17

Are small or larger p-values evidence against H₀? Provided?

Answer 17

Small, provided that there are other plausible hypotheses which would male the given outcome more likely

Question 18

How do you calculate a p-value?

Answer 18

P[𝒳² > V_α] = p٭

Question 19

What two values do we typically use when pre-assignign the p-value?

Answer 19

0.01 or 0.05

Question 20

What does n_ij, n_i. and n._j stand for?

Answer 20

• n_ij is the number of observations for which R = i, C = j
• n_i. is the number of observations with R = i
• n_.j is the number of observations with C = j

Question 21

What does π_ij, π_i., π_.j stand for?

Answer 21

• π_ij = P[R = i, C=j]
• π_i. = P[R = i]
• π_{.j =} = P[C=j]

Question 22

In the Chi-squared test for independence what is the null hypothesis, H₀?

Answer 22

πij = πi. x π.j

Question 23

In the Chi-squared test for independence how do we estimate πi. , π.j and πij?

Answer 23

Question 24

What is the test statistic in the Chi-squared test for independnce?

Answer 24

Question 25

What is the degrees of freedom in the Chi-squared test for independence?

Answer 25

(r - 1)(c - 1)

Question 26

If 𝒳² \< 𝒳²_(r-1)(c-1) what does the say about the independence of the rows and columns?

Answer 26

They are independent

Question 27

If 𝒳² \> 𝒳²_(r-1)(c-1) what does the say about the independence of the rows and columns?

Answer 27

They are not independent