Reading 55: Understanding Fixed-Income Risk and Return Flashcards
(17 cards)
Macaulay Duration
55.1
Understanding Fixed-Income Risk and Return
Where:
t = the number of days from the last coupon payment to the settlement date
T = the number of days in the coupon period
t/T = the fraction of the coupon period that has gone by since the last payment
PMT = the coupon payment per period
FV = the future value paid at maturity, or the par value of the bond
r = the yield to maturity, or the market discount rate, per period
N = the number of evenly spaced periods to maturity as of the beginning of the curent period

The Denominator of Macaulay Duration
55.1
Understanding Fixed-Income Risk and Return
It’s the PVFull of the bond including accrued interest!

Macauly Duration (revealed)
(combing eq 1 and 2)
55.3
Understanding Fixed-Income Risk and Return
The comination of the “main” Macaulay duration along with the PVfull reveals an important aspect of the Macaulay duration: Macaulay duration is a weighted average of the time to receipt of the bond’s promised payments, where the weights are the shares of the full price that correspond to each of the bond’s promised future payments.
The time to receipt of cash flow measured in terms of time periods are 1-t/T, 2-t/T, …, N-t/T. The weights are the present values of the cash flows divided by the full price. Therefore, Macaulay duration is measured in terms of time periods.

Macauly Duration (closed-form)
55.4
Understanding Fixed-Income Risk and Return
c is coupon rate per period (PMT/FV)
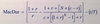
Modified Duration
55.5
Understanding Fixed-Income Risk and Return
It is MacDur divided by one plus the yield per period.
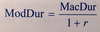
Using Modified duration to provide an estimate of the percentage price change for a bond given a change in its yield-to-maturity
55.6
Understanding Fixed-Income Risk and Return
The percentage price change refers to teh full price, including accrued interest.
The AnnModDur term is the annual modified duration, and
The deltaYield term is the change in the annual yield-to-maturity.
Minus sign means that bond prices and yields-to-maturity move inversely

Approximate Modified Duration
55.7
Understanding Fixed-Income Risk and Return
PV+ is the price when the yield is increased.
PV0 is original price
PV_ is wthe price when the yield-to-maturity is reduced.
The objective of the approximation is to estimate the slope of the line tangent to the price-yield curve.

Approximate Macaulay Duration
55.8
Understanding Fixed-Income Risk and Return
huh

Effective Duration
55.9
Understanding Fixed-Income Risk and Return
Teh effective duration of a bond is the sensitivity of hte bond’s price to a change in a benchmark yield curve.
The difference between approximate modified duration and effective duration is in the denominator. Modified duration is a yield duration statistic in that it measures interest rate risk in terms of a change in the bond’s own yield-to-maturity (DeltaYield).
Effective duration is a curve duration statistic in that it measures interest rate risk in terms of a parallel shift in the benchmark yield curve (DeltaCurve)

Money Duration
55.10
Understanding Fixed-Income Risk and Return
Calculated as the annual modified duration times the full price (PVfull) of the bond, including accrued interest.
The money duration of a bond is a measure of the price change in units of the currency in which the bond is denominated.

PVFull change estimated by MoneyDur
55.11
Understanding Fixed-Income Risk and Return
The estimated change in the bond price in currency units is calculated using this equation.

Price Value of a Basis Point (PVBP)
55.12
Understanding Fixed-Income Risk and Return
The PVBP is an estimate of the change in the full price given a 1 bp change in the YTM.
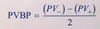
Convexity-adjusted estimate of the percentage change in the bond’s full price
55.13
Understanding Fixed-Income Risk and Return
The first bracketed expression, the “first-order” effect, is the same as 55.6.
The (annual) modified duration, AnnModDur, is multiplied by the change in the (annual) yield-to-maturity, DeltaYield.
The second bracketed expression, the “second order” effect, is the convexity adjustment. The convexity adjustment is the annual convexity statistic, AnnConvexity, times one-half, multiplied by the change in the YTM squared. This additional term is a positive amount on a traditional (option-free) fixed-rate bond for either an increase or decrease in the yield.

Approximate Convexity (ApproxCon)
55.14
Understanding Fixed-Income Risk and Return

Convexity (of a zero-coupon bond)
55.15
Understanding Fixed-Income Risk and Return
The Macaulay duration of a zero-coupon bond is N - t/T in terms of periods to maturity.
N is the number of periods to maturity as of the beginning of the current period, t/T is the fraction of the period that has gone by, and r is the yield-to-maturity per period.

Money Convexity
55.16
Understanding Fixed-Income Risk and Return
The money duration of a bond indicates the first-order effect on the full price of a bond in units of currency given a change in the YTM. The money convexity statistic (MoneyCon) is the second-order effect. The money convexity of the bond is the annual convexity multiplied by the full price, such that

Effective Convexity
55.17
Understanding Fixed-Income Risk and Return
The effective convexity of a bond is acurve convexity statistic that measures the secondary effect of a change in a benchmark yield curve.
A pricing model is used to determine the new prices when the benchmark curve is shifted upward (PV+) and downward (PV_) BY THE SAME AMOUNT (delta curve).
These changes are made holding other factors constant - for example, teh credit spread.



