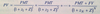Reading 53: Introduction to Fixed-Income Valuation Flashcards
(15 cards)
Present Value for Bond Price
(given market discount rate)
53.1
Intro to Fixed-Income Valuation
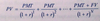
Present Value for Bond Price
(given sequence of spot rates)
53.2
Intro to Fixed-Income Valuation
Where:
Z1 = spot rate, or the zero-coupon yield, or zero rate, for Period 1
Z2 = spot rate, or the zero-coupon yield, or zero rate, for Period 2
ZN = spot rate, or the zero-coupon yield, or zero rate, for Period N
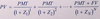
PVFull Equation
53.3
Intro to Fixed-Income Valuation

Accrued Interest
53.4
Intro to Fixed-Income Valuation
Where:
t = number of days from the last coupon payment to the settlement date
T = number of days in the coupon period
t/T = fraction of the coupon period that has gone by since the last payment
PMT = coupon payment per period
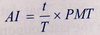
The full price of a fixed-rate bond between coupon payments given the market discount rate per period (r)
(PV Full expanded)
53.5
Intro to Fixed-Income Valuation
Similar to normal PV formula, but the difference is that the next coupon payment (PMT) is discounted for the remainder of thecoupon period, which is 1 - t/T. The second coupon payment is discounted for that fraction plus another full period, 2 - t/T.
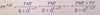
PVFull simplified
53.6
Intro to Fixed-Income Valuation
Uses PV
NOT PVFlat
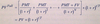
Convert Annual Percentage Rate for m periods per year to APR for n periods per year
53.7
Intro to Fixed-Income Valuation

FRN Pricing Model
(required margin is discount margin)
53.8
Intro to Fixed-Income Valuation
Where:
PV = present value, or price of the floating-rate note
Index = reference rate, stated as an annual percentage rate
QM = quoted margin, stated as an annual percentage rate
FV = future value paid at maturity, or the par value of the bond
m = periodicity of the floating-rate note, the number of payment periods per year
DM = discount margin, the required margin stated as an annual percentage rate
N = number of evenly spaced periods to maturity

Pricing formula for money market instruments on a discount rate basis
53.9
Intro to Fixed-Income Valuation
Where:
PV = present value, or price of the money market instrument
FV = future value paid at maturity, or face value of the money market instrument
Days = number of days betseen settlement and maturity
Year = number of days in the year
DR = discount rate, stated as an annual percentage rate
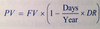
Formula for DR for money market instrument
53.10
Intro to Fixed-Income Valuation
Where:
PV = present value, or price of the money market instrument
FV = future value paid at maturity, or face value of the money market instrument
Days = number of days betseen settlement and maturity
Year = number of days in the year
DR = discount rate, stated as an annual percentage rate

Pricing formula for money market instrumetn quoted on an add-on rate basis
53.11
Intro to Fixed-Income Valuation
Where:
PV = present value, pricipal amount, or price of the money market instrument
FV = future value, or the redemption amount paid at maturity including interest
Days = number of days betseen settlement and maturity
Year = number of days in the year
AOR = add-on rate, stated as an annual percentage rate
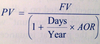
Formula for isolated AOR term
53.12
Intro to Fixed-Income Valuation
Where:
PV = present value, pricipal amount, or price of the money market instrument
FV = future value, or the redemption amount paid at maturity including interest
Days = number of days betseen settlement and maturity
Year = number of days in the year
AOR = add-on rate, stated as an annual percentage rate

Equation for calculating a par rate given a sequence of spot rates
(based on par curve)
53.13
Intro to Fixed-Income Valuation
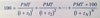
Relationship between two spot rates and the implied forward rate
53.14
Intro to Fixed-Income Valuation
A = shorter-term bond periods to maturity
B = longer-term bond periods to maturity
zA = YTM per period on bond A
zB = YTM per period on bond B
The first is an A-period zero-coupon bond trading in the cash market. The second is a B-period zero-coupon cash market bond.
The implied forward rate between period A and period B is denoted IFRA,B-A
It is a forward rate on a security that starts in period A and ends in period B. Its tenor is B - A periods.

Zero Volatility Spread (Z-spread) of a bond over the benchmark rate
53.15
Intro to Fixed-Income Valuation
The benchmark spot rates z1, z2, …, zN are derived from the government hyield curve (or from fixed rates on interest rate swaps).
Z is the Z-spread per period and is the same for all time periods.
N is an integer, so the calculation is on a coupon date when the accrued interest is zero.