Radiobiology 1 Flashcards
How does radiation damage cells?
- Ionising radiation stops cell division by inducing non-repairable, i.e. lethal, lesions on the DNA strand. IR causes breaks in the chemical bonds of DNA.
- Damage can be direct or indirect
- Indirect: water molecule is ionised producing a hydroxyl (OH●) free radical and fast electrons i.e. a molecule with an unpaired electron in the valence shell, which leads to the molecule being very reactive
Damage Repair:
Single strand breaks
Double strand breaks
Single strand breaks
- Graduall repeaired using the undamaged strand as a template
- Exponential repair rate with half life (1.5hours normal tissue, 0.5hours tumour tissue)
- After 24 hour fraction, sub-lethal single strand damage is pretty much all repaired
Double strand breaks
- Lethal damage because there is no longer a template to copy from
- Can be single event or double event
Linear Quadratic rationale)
- GO THROUGH THE MATHS ON THE SLIDE
- Both strands broken at same level = irreparable damage
- Mean number of DSBs by 1 hit/cell increases linearly with dose = ad
- Mean number of DSBs by 2 independent hits/cell = (mean numbr of hhits/cell) * (mean number of sites/cell already hit) -> increases quadriatically with dose = Bd^2
How do you find a/B ratio from a SF graph?

- At the point when ad=Bd^2 -> d = a/b
- At the point where there are an equal number of DSBs from single events and two independent events, the dose at which there is equal cell kill from single events and two independent events.
- But you don’t normally have a graph of where the two lines cross
- You have to note tha tthe plot of the beta component starts off horizontal ( as d tends to 0, the b survival curve tends to 0) and the total SF is dominated by the alpha component
- Draw tangent from straight part of line (alpha component)
- At the point where the distance between the tangent and the axis is equal to the distance from the tangent to the SF, d=alpha/beta
Typical a/b ratio
- Tumour (ealry)
- Normal (late)
- central nervous system
- lung
- Tumour (ealry) - 10
- Normal (late) - 3
- central nervous system - 2
- lung - 4
Effect of fractionation on survival curve
How does survival curve look for normal (late) and tumour (early) tissue?
How does a/b ratio relate to fractionation sensitivity?
- Tumour has higher a/b ratio and higher a, less curvature on survival fraction. Higher intiial gradient (i.e. more radiosensitive than normal tissues to small dose fractions
- If you give sufficent time between fractions for repair of sub-lethal damage, starting shape of curve repeats and survival advantage for normal tissue is retained
- a/b ratio is measure of fractionation sensitivy and repair capacity
- Low a/b -> greater fractionation sensitivity, SF has more curvature, and dose is stronger function of fractionation. Also, greater repair capacity (less damage when fractionated)
NB// Preferentially spare late reacting tissue by giving many small fractions
Things to note when drawing fractionated survival curve
DO THE EXCEL FILE ON THE TUTORIAL

- LAte reacting tissue is more sensitive to fraction size, gradient changes faster with increasing dose
- First fraction is same as single dose of same size, no difference between fractionated and single dose curves
- Each fraction repeats fractional loss of first fraction (ruler between inflection points)
- Initial gradient largely depends on alpha, which is not the same from late and early tissues, hence the lines are different
- Data on fractionated plot shoould be made of data points (you don’t have data at sub-fraction intervals)
Biologically Effective Dose
- How do you get from SF to BED?
- Why do you want to do this?
- What is it?
- Eqn?
- Divide through by -alpha
- Gives you a quantity in units of dose
- BED is not physical dose, it is a convenient measure of comparritive effect of fifferent dose/fractionation regimes
- BED = D [1+ d/(a/b)]
- d = dose from single fraction, D = nd = total dose
What’s the difference between 60Gy in 30# and 58.8Gy in 28# ?
BED = D [1+ d/(a/b)]
NORMAL TISSUE
- 60 [1 + 2/3] = 100
- 58.8 [1 + 2.1/3] = 100
TUMOUR TISSUE
- 60[1 + 2/10] = 72
- 58.8 [1 + 2.1/10] = 71.1
What is Tumour Control Probability?
SEE PPT FOR EQUATION
The fraction of tumours with no active clonogenic cells after all treatment which will equal the fraction of patients with Local Control
- TCP = exp(-k) = exp(-k0SF) k = cancer cells after RT, Ko = cancer cells before RT
- SF = exp(-a*BED)
- TCP = exp(-k) = exp(-k0SF) = exp(-k0exp(-a*BED))
What happens to TCP curve:
ko increases
a increases
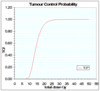
- Ko increases, i.e. more cancer cells at start oif treatment, whole curve moves right, you need more dose to get control
- As alpha increases, curve moves left and becomes steeper
What does TD5/5 lung = 20Gy mean?
there is a 5% probability of lung pneumonitis after 5 years following a dose of 20 Gy to the whole lung in 2 Gy fractions
Uncomplicated Control Probability - Label lines

- Black - Absence of normal tissue complication
- Green - TCP
- Brown - Normal tissue complication
- Blue - Uncomplicated control probability
Why do you need a proliferation correction?
- RT improves environment for tumour cells, remaining cells preliferate more rapidly than normal tumours
- PC takes into account BED loss due to tumour proliferation
- Only have PC for early/tumour effects
- Repopulation is constant fractional increase in tumour cells per unit time i.e. an exponential increase eγt (γ takes the form ln2/Tp ).
- Tpot = potential doubling time
Equation for proliferation correction?
How do SF anf BED depend on Tp?
Why is this important?
SF = exp( -D(a+bd) ) * exp gammaT
gamma = ln(2) / Tpot
BED = -ln(SF)/a = D[1+d/(a/b)] - gammaT/a
Delaying treatment gives time for tumour to recover rapidly (2Gy fraction lost per week fo delay).
But it only starts to happen after a delay in time,
SELF TEST QUESTIONS AT THE END OF THIS PPT
&
TUTORIALS
&
EXCEL SPREADSHEET


